Quaternion kinematics for the error-state Kalman filter论文阅读

0. 参考文献

【１】Quaternion kinematics for the error-state Kalman filter

四元数基础参考之前的一片博文

1. 四元数的定义和属性

1.1 四元数的定义

1.1.1 四元数的表示方式

1.2 四元数的性质

1.2.1 加和

1.2.2 积

1.2.3 单位１

1.2.4 共轭

1.2.5 长度

1.2.6 逆

1.2.7 单位四元数

1.3 额外的性质

1.3.1 quaternion commutator

1.3.2 纯四元数的乘积

1.3.3 纯四元数的幂

1.3.4 纯四元数的指数

1.3.5 一般四元数的指数

1.3.6 单位四元数的对数

1.3.7 一般四元数的对数

1.3.8 四元数的幂的指数形式

2. 旋转和cross-relations

2.1 ３维向量的旋转

如下图的旋转：

可以将ｘ分解：

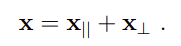
分解后各个成分的计算方法：

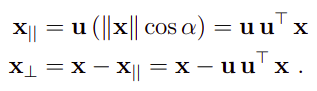
在旋转的过程中，和轴平行的部分不发生变化：

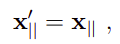
在垂直于旋转轴的平面上选择两个基向量：

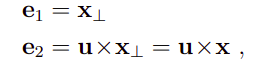
在该平面内旋转$\varphi$角度后，有：

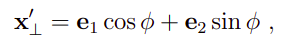
可以写做：

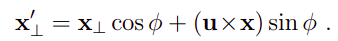
再加上平行的部分，可以得到旋转后的整体向量：

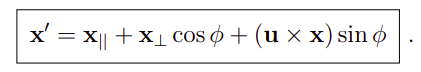
注意这里要区别上一篇博文中的一个公式：

仔细观察和计算可以发现两个式子其实是一样的，只不过表达的符号并不相同。

2.2 旋转群SO3

旋转变换会保持向量长度：

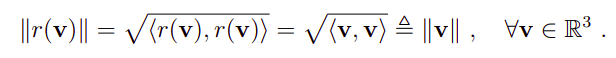
旋转变换会保持两线夹角：

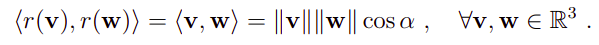
旋转变换会保持向量间方向关系：

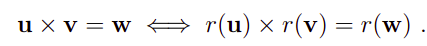
这一章就是要说明旋转群和四元数之间的关系？
首先有如下一个表：

2.3 旋转群和旋转矩阵

将旋转变换写成一个矩阵形式：

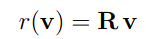
旋转矩阵不改变向量长度，说明Ｒ是正交的：

进一步将正交性质写成　：

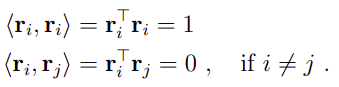
同时说明：

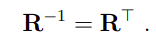
由于上面说过，Ｒ有保持向量方向的特性，因此有如下的关系，这个用来排除了反射这一类特殊矩阵：

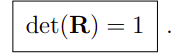
2.3.1 指数映射

这里引出了李代数

2.3.2 大写的指数映射

这里是换一种表达方式

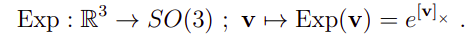
2.3.3 旋转矩阵和旋转向量：罗德里格斯公式

2.3.4 对数映射

又映射回去

2.3.5 旋转变换

2.4 旋转群和四元数

先做一个假设（后面会证明，其实上一篇博文对应的文献也有证明）

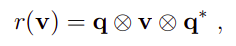
由于旋转保持了向量v的长度，并且根据四元数的性质，有：

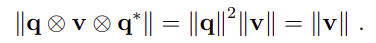
为了满足上式成立，需要q的模等于1：

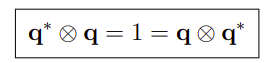
可以看到，这个条件，和前面在描述旋转矩阵时的条件，类似，就是下面这个：

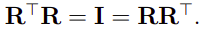
下面证明四元数旋转能保持向量x乘方向，证明过程运用了两次1.3.1里面的性质

2.4.1

2.4.2 大写的指数映射

2.4.3 四元数和旋转向量

2.4.4 对数映射

2.4.5 旋转变换

2.4.6 The double cover of the manifold of SO3

2.5 旋转矩阵和四元数

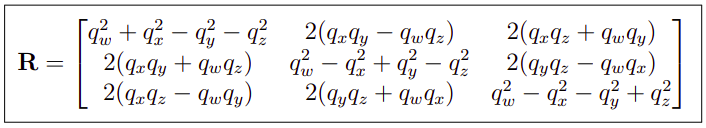
2.6 组合多个旋转

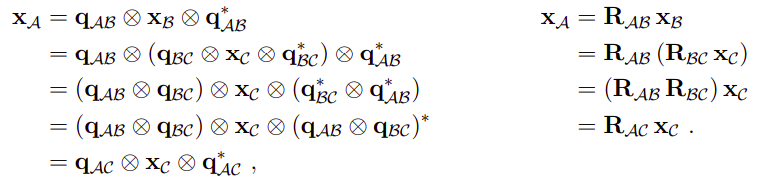
2.7 球面线性插值（ＳＬＥＲＰ）

2.8 quaternion and isoclinic rotations:explaining the magic

3. Quaternion conventions. MY choice

4. Perturbations, derivatives and integrals

4.1 在SO3上的加法减法

4.2 the four possible derivative definitions

4.2.1 从向量空间到向量空间

这个是在向量空间上的求导数定义

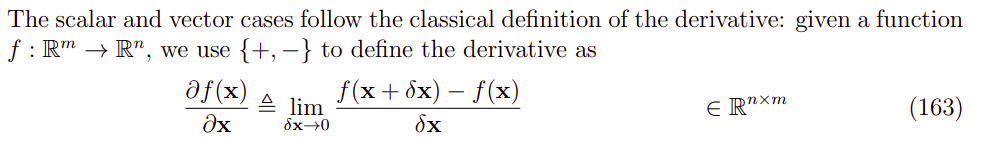
一阶泰勒展开（或者看成欧拉积分）：

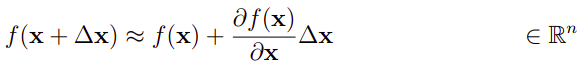
4.2.2 从SO3到SO3

4.2.3 从向量空间到SO3

4.2.4 从SO3到向量空间

4.3 有用的旋转雅阁比

考虑要对一个向量$a\text{a}a$进行旋转，旋转轴为$u\text{u}u$，旋转角度$\theta$，考虑三种不同形式的表达：$\theta \text{θ}\theta =\theta u\text{u}u$， q = q { θ } \pmb{q=q\{\theta\}} q=q{θ}​q=q{θ}​​q=q{θ}， R = R { θ } \pmb{R=R\{\theta\}} R=R{θ}​R=R{θ}​​R=R{θ}。我们关心的是旋转结果对于不同旋转度量的雅阁比

4.3.1 对于向量(vector)的雅阁比

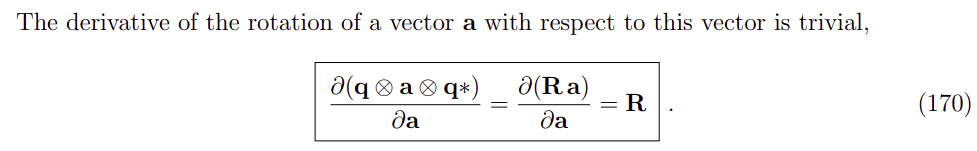
4.3.2 对于四元数的雅阁比

4.3.3 SO3空间的右乘雅阁比

4.3.4 对于旋转向量的雅阁比

注意这一节和《slam十四讲》的内容进行对应，注意区别和联系

上面这一段和《十四讲》中下面这一段是一样的：

4.4 扰动，不确定性和噪声

4.4.1 local perturbations

在原先的四元数ｑ上加一个微小的扰动量：

下面这一大段其实每太看懂，其中提到的泰勒展开，和《十四讲》里的扰动模型推导过程应该也有些关系

4.4.2 Global perturbations

完全看不懂要干啥

4.6 Time-integration of rotation rates

4.6.1 零阶积分

4.6.2 一阶积分

5. Error-state Kinematics for IMU-driven system

5.1 motivation

5.2 eskf 解释

我们考虑error因为它小，可以很容易线性化。那些较大的值就直接积分好了。

那些高频的IMU数据，被积分成状态，这些状态没考虑误差和模型的不确定性，因此，有较大的积累误差。这些误差会通过动态方程进行估计，然后去修正积分值。

5.3 连续时间的系统运动学

所有的定义变量：


注意：
（1）IMU直接读的角速度是local坐标系下的
（2）角度偏差也是local的

5.3.1 真实状态运动学

这里面包含了输入随机误差
真实状态运动学方程为：

5.3.2 名义状态运动学

这里面没有包含随机误差和扰动：

5.3.3 误差状态运动学

误差的状态变化方式

先看式（238a，238d，238e，238f），以（238a）为例展示推导过程：
根据上面的表，已知$p_t=p+\delta p$，两边求导得${\dot{p}}_t=\dot{p}+\dot{\delta p}$，查上表，代入几个p的表达式，就可以得到$\dot{\delta p}$的表达式。

再看式（238b）线速度误差。我们要确定线速度误差的变化率$\dot{\delta v}$，从下面的关系开始：


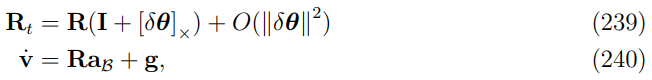
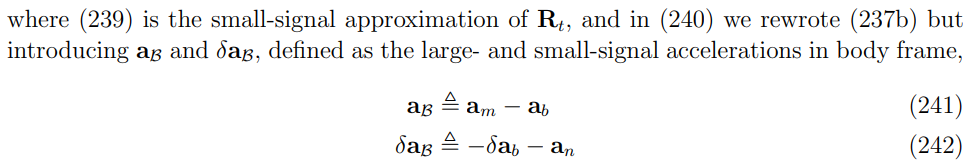
然后开始处理${\dot{\delta v}}_t$:

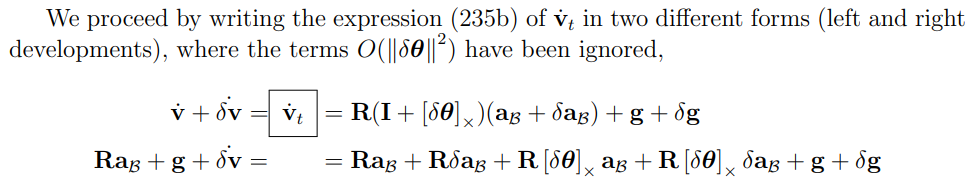
第一行式子展开了右侧，第二行把左侧展开了，左右对消，可以得到

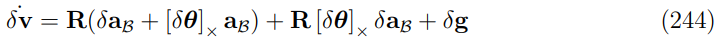
删除高阶项：

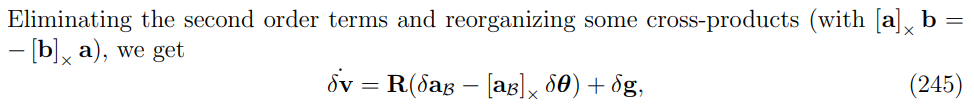
将前面的式子带进来：

注意这里面的$a_n$项，这个是噪声，线加速度噪声和旋转无关，因此：

再看方向偏差变化率，我们要确定的是$\dot{\delta \theta }$，从下面的关系开始：

上面的分别真实状态，和名义状态。和线加速度一样，写成大信号和小信号的形式：

两个合起来就是：

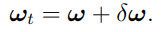
进一步处理真实四元数的导数

移项并化简：

得到两个方程：

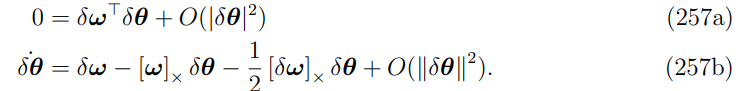
第一个不是很有用，主要看第二个，忽略高阶项后：

进一步化简：

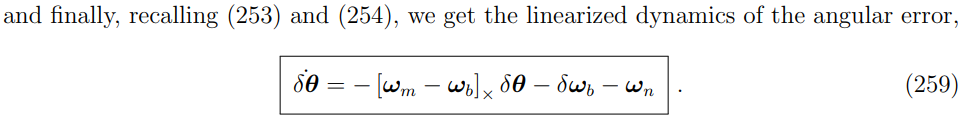
5.4 离散时间的系统运动学

要将上面的微分方程离散化，有的可以直接离散，有的可能要用到数值积分方法。仅针对名义状态和误差状态进行离散化：

5.4.1 名义状态运动学

得到的离散运动方程如下，也可以用其他的积分方法？

5.4.2 误差状态运动学

需要回忆一下卡尔曼滤波

5.4.3 误差状态雅阁比和扰动

6. 融合其他的传感器信息

用IMU信息来预测，用其他的信息来矫正filter，进而观测到IMU的偏置误差，矫正过程如下：

1. 通过滤波器矫正来观测到error-state
2. 将观测到的error注入到名义状态
3. 重置error-state

6.1 通过滤波器矫正来观测到error-state

假设有一个观测模型：

其中h是关于真实状态的非线性函数，v是一个高斯噪声

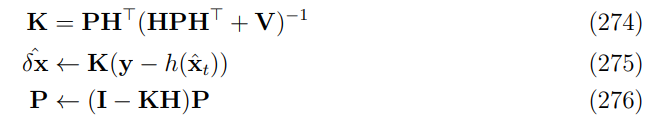
6.1.1 滤波器矫正的雅阁比计算

6.2 观测误差注入名义状态

6.3 ESKF 重置

6.3.1 重置操作中关于方向误差的雅阁比计算