PX4飞控中利用EKF估计姿态角代码详解
PX4飞控中主要用EKF算法来估计飞行器三轴姿态角,具体c文件在px4\Firmware\src\modules\attitude_estimator_ekf\codegen\目录下
- 具体原理
- 程序详解
- 下一步
1.具体原理
EKF算法原理不再多讲,具体可参见上一篇blog http://blog.csdn.net/lizilpl/article/details/45289541.
这篇讲EKF算法执行过程,需要以下几个关键式子:
飞行器状态矩阵:
这里
表示三轴角速度,
表示三轴角加速度,
表示加速度在机体坐标系三轴分量,
,表示磁力计在机体坐标系三轴分量。
测量矩阵
分别由三轴陀螺仪,加速度计,磁力计测得。
状态转移矩阵:
飞行器下一时刻状态预测矩阵如下:
其中W项均为高斯噪声,
为飞行器在姿态发生变化后,坐标系余旋变换矩阵,对该函数在
处求一阶偏导,可得到状态转移矩阵:
此时可得到飞行器状态的先验估计:
利用测量值修正先验估计:
这里测量矩阵H与状态矩阵X为线性关系,故无需求偏导。
卡尔曼增益:
状态后验估计:
方差后验估计:
2.程序详解
整个EKF的代码挺长的,大部分是矩阵运算,而且使用嵌套for循环来执行的,所以读起来比较费劲,但是要是移植到自己工程上的话必然离不开这一步,所以花了一个下午把各个细节理清楚,顺便记录分享。
/* Include files */
#include "rt_nonfinite.h"
#include "attitudeKalmanfilter.h"
#include "rdivide.h"
#include "norm.h"
#include "cross.h"
#include "eye.h"
#include "mrdivide.h"
/*
'输入参数:updateVect[3]:用来记录陀螺仪,加速度计,磁力计传感器数值是否有效
z[9] :测量矩阵
x_aposteriori_k[12]:上一时刻状态后验估计矩阵,用来预测当前状态
P_aposteriori_k[144]:上一时刻后验估计方差
eulerAngles[3] :输出欧拉角
Rot_matrix[9] :输出余弦矩阵
x_aposteriori[12] :输出状态后验估计矩阵
P_aposteriori[144] :输出方差后验估计矩阵'
*/
void attitudeKalmanfilter(
const uint8_T updateVect[3],
real32_T dt,
const real32_T z[9],
const real32_T x_aposteriori_k[12],
const real32_T P_aposteriori_k[144],
const real32_T q[12],
real32_T r[9],
real32_T eulerAngles[3],
real32_T Rot_matrix[9],
real32_T x_aposteriori[12],
real32_T P_aposteriori[144])
{
/*以下这一堆变量用到的时候再解释*/
real32_T wak[3];
real32_T O[9];
real_T dv0[9];
real32_T a[9];
int32_T i;
real32_T b_a[9];
real32_T x_n_b[3];
real32_T b_x_aposteriori_k[3];
real32_T z_n_b[3];
real32_T c_a[3];
real32_T d_a[3];
int32_T i0;
real32_T x_apriori[12];
real_T dv1[144];
real32_T A_lin[144];
static const int8_T iv0[36] = { 0, 0, 0,
0, 0, 0,
0, 0, 0,
1, 0, 0,
0, 1, 0,
0, 0, 1,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0 };
real32_T b_A_lin[144];
real32_T b_q[144];
real32_T c_A_lin[144];
real32_T d_A_lin[144];
real32_T e_A_lin[144];
int32_T i1;
real32_T P_apriori[144];
real32_T b_P_apriori[108];
static const int8_T iv1[108] = { 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1 };
real32_T K_k[108];
real32_T fv0[81];
static const int8_T iv2[108] = { 1, 0, 0, 0, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0, 0, 0, 0,
0, 0, 1, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 1, 0, 0, 0, 0, 0,
0, 0, 0, 0, 1, 0, 0, 0, 0,
0, 0, 0, 0, 0, 1, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 0, 0,
0, 0, 0, 0, 0, 0, 0, 1, 0,
0, 0, 0, 0, 0, 0, 0, 0, 1 };
real32_T b_r[81];
real32_T fv1[81];
real32_T f0;
real32_T c_P_apriori[36]=
{ 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 1, 0, 0,0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0 };
real32_T fv2[36];
static const int8_T iv4[36] = { 1, 0, 0,
0, 1, 0,
0, 0, 1,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0 };
real32_T c_r[9];
real32_T b_K_k[36];
real32_T d_P_apriori[72];
static const int8_T iv5[72]
= { 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0 };
real32_T c_K_k[72];
static const int8_T iv6[72] = { 1, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0,
0, 0, 1, 0, 0, 0,
0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0,
0, 0, 0, 1, 0, 0,
0, 0, 0, 0, 1, 0,
0, 0, 0, 0, 0, 1,
0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0 };
real32_T b_z[6];
static const int8_T iv7[72]
= { 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1 };
static const int8_T iv8[72]
= { 1, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0,
0, 0, 1, 0, 0, 0,
0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0,
0, 0, 0, 1, 0, 0,
0, 0, 0, 0, 0, 1 };
real32_T fv3[6];
real32_T c_z[6];
/*开始计算*/
/*'wak[]为当前状态三轴角加速度'*/
wak[0] = x_aposteriori_k[3];
wak[1] = x_aposteriori_k[4];
wak[2] = x_aposteriori_k[5];/* ‘欧拉角旋转矩阵’
这里的O矩阵相当于A矩阵中的
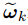 的转置矩阵!
的转置矩阵!
*/
O[0] = 0.0F;
O[1] = -x_aposteriori_k[2];
O[2] = x_aposteriori_k[1];
O[3] = x_aposteriori_k[2];
O[4] = 0.0F;
O[5] = -x_aposteriori_k[0];
O[6] = -x_aposteriori_k[1];
O[7] = x_aposteriori_k[0];
O[8] = 0.0F;
/* 预测转过一个小角度之后的重力向量三轴投影 */
/* a = [1, -delta_z, delta_y;
* delta_z, 1 , -delta_x;
* -delta_y, delta_x, 1 ]'; */
eye(dv0); //dv0矩阵单位化
for (i = 0; i < 9; i++) {
a[i] = (real32_T)dv0[i] + O[i] * dt;
}
/* 预测转过一个小角度之后的磁力向量三轴投影 */
eye(dv0);
for (i = 0; i < 9; i++) {
b_a[i] = (real32_T)dv0[i] + O[i] * dt;
}
/*
其实就是这个大家都很眼熟的的余弦矩阵的转置, 用来更新机体转过一个角度之后的重力和磁力三轴投影,只不过两次计算间隔时间很短,变化角度很小,因此忽略高阶小量之后就变成了这个样子。这里还少一个时间系数dt,下面会补上。
*/
x_n_b[0] = x_aposteriori_k[0]; //角速度
x_n_b[1] = x_aposteriori_k[1];
x_n_b[2] = x_aposteriori_k[2];
b_x_aposteriori_k[0] = x_aposteriori_k[6]; // 加速度
b_x_aposteriori_k[1] = x_aposteriori_k[7];
b_x_aposteriori_k[2] = x_aposteriori_k[8];
z_n_b[0] = x_aposteriori_k[9]; //磁力计
z_n_b[1] = x_aposteriori_k[10];
z_n_b[2] = x_aposteriori_k[11];
for (i = 0; i < 3; i++) {
c_a[i] = 0.0F;
for (i0 = 0; i0 < 3; i0++) {
c_a[i] += a[i + 3 * i0] * b_x_aposteriori_k[i0];
}
d_a[i] = 0.0F;
for (i0 = 0; i0 < 3; i0++) {
d_a[i] += b_a[i + 3 * i0] * z_n_b[i0];
}
x_apriori[i] = x_n_b[i] + dt * wak[i];
}
for (i = 0; i < 3; i++) {
x_apriori[i + 3] = wak[i];
}
for (i = 0; i < 3; i++) {
x_apriori[i + 6] = c_a[i];
}
for (i = 0; i < 3; i++) {
x_apriori[i + 9] = d_a[i];
} //得到状态先验估计 /*
根据上述矩阵运算,可以得到:
从而:








 本文详细解析了PX4飞控如何利用扩展卡尔曼滤波(EKF)算法估计飞行器的姿态角。内容包括EKF的执行过程,关键公式,以及代码实现中的矩阵运算。通过对状态矩阵、测量矩阵、状态转移矩阵的讨论,阐述了飞行器状态的先验和后验估计。最后,文章预告将把理解后的EKF算法应用到实际工程中。
本文详细解析了PX4飞控如何利用扩展卡尔曼滤波(EKF)算法估计飞行器的姿态角。内容包括EKF的执行过程,关键公式,以及代码实现中的矩阵运算。通过对状态矩阵、测量矩阵、状态转移矩阵的讨论,阐述了飞行器状态的先验和后验估计。最后,文章预告将把理解后的EKF算法应用到实际工程中。
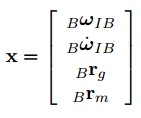
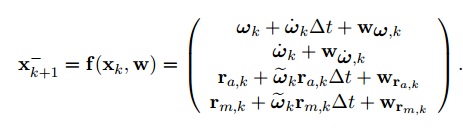
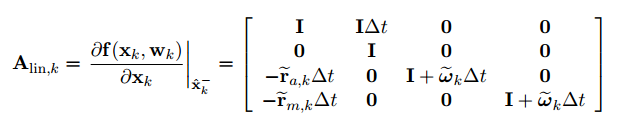
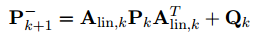
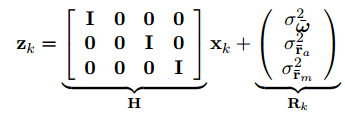
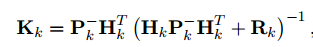
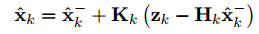
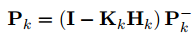
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 6330
6330

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








