离散数学 | 图论 五色定理证明

看来一下午终于看懂了，甚至差点睡过去…… 趁热打铁记录一下自己的理解。

平面图的五色定理

任意一个简单的连通平面图点着色至多五色。

前置知识

一、 设 G 为一个至少有三个结点的连通平面图，则 G 中必有一个结点 u，u 的度数 deg(u)≤5。

五色定理 证明

Step1：证明简单连通平面图 G 中一定存在一个顶点，其度数小于等于 5。

根据前置知识一得证。

Step2：归纳假设

当 |V|≤5 时：

此时可对每个顶点任意着色，总着色数显然不超过 5。

当 |V|>5 时：

一、 假设当 |V|=k 时，结论成立。

二、 当 |V|=k+1 时，由 Step1 可知，G 中必存在一点 u 满足 deg(u)≤5。将 u 从图 G 中删去，则 |V|=k+1-1=k 符合一中假设，G-u 可用 5 种颜色着色。

将 u 放回图中恢复图 G，对 u 的着色进行分类讨论：

1. 【deg(u)<5】 或 【deg(u)=5 且点 u 连接的 5 个结点所着颜色小于 5】，则点 u 可着第 5 种颜色。
2. deg(u)=5 且 点 u 连接的 5 个结点着 5 种不同的颜色。假设五种颜色分别为红、黄、蓝、白、绿：
   
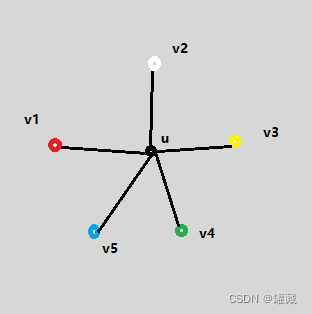
   约定图 G-u 中所有着红、黄色的结点组成红黄集，着白、绿色的结点组成白绿集。分情况讨论：
   • $v_1,v_3$ 属于红黄集导出的、G 的子图的、两个不同的连通分支。
     
     将 $v_1$ 所在连通分支中的红、黄色对调，并不影响 G-u 的着色。则 u 点可着红色。
     此时图 G 可正常着色。
   • $v_1,v_3$ 属于红黄集导出的、G 的子图的、同一个连通分支，则 $v_1,v_3$ 之间必有一条由红黄集中结点构成的路 P，它加上 u 可构成一个回路 C(u,P,u)。
     
     由于 G 是平面图，因此，回路 C 会将白绿集分成两个子集，分别位于 C 的内外。这样白绿集导出的子图至少有两个连通分支，从而将问题转换为上一类问题，即将 $v_2$ 所在连通分支中的白、绿色对调，并不影响 G-u 的着色。则 u 点可着白色。
     此时图 G 可正常着色。
   • $v_1,v_3$ 属于红黄集导出的、G 的子图的、同一个连通分支，则 $v_1,v_3$ 之间必有一条由红黄集中结点构成的路 P，它加上 u 可构成一个回路 C(u,P,u)。
     $v_2,v_4$ 属于白绿集导出的、G 的子图的、同一个连通分支，则 $v_2,v_4$ 之间必有一条由白绿集中结点构成的路 Q，它加上 u 可构成一个回路 C(u,Q,u)。
     
     此时因为红黄集和白绿集组成的两个连通分支中结点不相邻，可直接将白色换为红色，绿色换位黄色。则 u 可着白色或绿色，图 G 总着色数为 4 小于 5。满足结论。

参考

【离散数学】图论 第七章(6) 图的结点着色和Welch Powell法、平面图着色、希伍德五色定理、四色定理-memcpy0-CSDN