经纬高(LLA)坐标系地心地固(ECEF)坐标系与东北天(ENU)坐标系转换

        前段时间在做水下机器人项目，添加了RTK，读取到的数据为经纬高坐标系中度分形式的经纬度信息，无法直接用于定位，还需要进行坐标系的转换。后来在学习Cartographer时处理GPS数据也有提到这方面的知识，于是决定汇总到一起进行学习，下文将对相关内容进行介绍。

一.LLA坐标系与ECEF坐标系之间的转换

        其中lon为经度信息，lat为纬度信息，alt为高度信息，f为极扁率，N为基准椭球体的曲率半径，将传入的信息先转换为ECEF坐标系下的X Y Z

        当已知ECEF坐标系下点为(x,y,z)时，需转换为LLA坐标系下的(lon,lat,alt)：

       最初lon是未知的，可以假设为0，经过计策迭代之后就能收敛。

二.ECEF坐标系转ENU坐标系

        ECEF坐标系原点为地球的质心，x轴延伸通过本初子午线和赤道的交点。 z轴延伸通过的北极（即与地球旋转轴重合）。 y轴完成右手坐标系，穿过赤道和90度经度。

         坐标原点(),目标点P(x,y,z),以为坐标原点的东北天坐标系坐标(e,n,u)，LLA坐标系下的坐标 ()，其中S为正交矩阵：

        而从ENU坐标系转换到ECEF坐标系为：

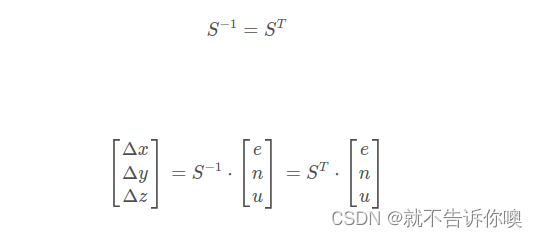
       以下Cartographer代码中，为计算第一帧GPS数据指向ECEF坐标系下原点的坐标变换：

cartographer::transform::Rigid3d ComputeLocalFrameFromLatLong(
    const double latitude, const double longitude) {
  const Eigen::Vector3d translation = LatLongAltToEcef(latitude, longitude, 0.);
  const Eigen::Quaterniond rotation =
      Eigen::AngleAxisd(cartographer::common::DegToRad(latitude - 90.),
                        Eigen::Vector3d::UnitY()) *
      Eigen::AngleAxisd(cartographer::common::DegToRad(-longitude),
                        Eigen::Vector3d::UnitZ());
  return cartographer::transform::Rigid3d(rotation * -translation, rotation);
}

        首先调用的是LatLongAltToEcef函数，从名字不难猜到这个函数是用来将得到的经纬高坐标系下的经纬度坐标转换成ECEF坐标系下的坐标：

Eigen::Vector3d LatLongAltToEcef(const double latitude, const double longitude,
                                 const double altitude) {
  // note: 地固坐标系(Earth-Fixed Coordinate System)也称地球坐标系, 
  // 是固定在地球上与地球一起旋转的坐标系.
  // 如果忽略地球潮汐和板块运动, 地面上点的坐标值在地固坐标系中是固定不变的.

  // https://en.wikipedia.org/wiki/Geographic_coordinate_conversion#From_geodetic_to_ECEF_coordinates
  
  constexpr double a = 6378137.;  // semi-major axis, equator to center.
  constexpr double f = 1. / 298.257223563;
  constexpr double b = a * (1. - f);  // semi-minor axis, pole to center.
  constexpr double a_squared = a * a;
  constexpr double b_squared = b * b;
  constexpr double e_squared = (a_squared - b_squared) / a_squared;
  const double sin_phi = std::sin(cartographer::common::DegToRad(latitude));
  const double cos_phi = std::cos(cartographer::common::DegToRad(latitude));
  const double sin_lambda = std::sin(cartographer::common::DegToRad(longitude));
  const double cos_lambda = std::cos(cartographer::common::DegToRad(longitude));
  const double N = a / std::sqrt(1 - e_squared * sin_phi * sin_phi);
  const double x = (N + altitude) * cos_phi * cos_lambda;
  const double y = (N + altitude) * cos_phi * sin_lambda;
  const double z = (b_squared / a_squared * N + altitude) * sin_phi;

  return Eigen::Vector3d(x, y, z);
}

        回到ComputeLocalFrameFromLatLong函数，rotation为ECEF坐标系下的坐标到 local 坐标系的旋转矩阵，translation 表示ECEF坐标系原到 (latitude, longitude) 位置的平移，该旋转矩阵表示先绕Y轴调整经度，然后再绕Z轴调整纬度。