雷达方程.

最新推荐文章于 2024-09-11 16:40:14 发布

m0_62546127

最新推荐文章于 2024-09-11 16:40:14 发布

阅读量1.9k

点赞数 2

分类专栏：雷达原理文章标签：信号处理

本文链接：https://blog.csdn.net/m0_62546127/article/details/134196001

版权

雷达原理专栏收录该内容

7 篇文章

订阅专栏

雷达方程在前面雷达发射机和接收机的部分都涉及到了，但是我觉得自己的理解思路很乱，在之前的博客里讲的也不是很清楚，所以干脆把“雷达作用距离”这一章提到前面来，重点放在雷达方程这一部分。

雷达方程又叫”雷达最大作用距离方程“，顾名思义，它指出了雷达可以探测到目标的最大距离。

基本雷达方程

之前我们一直用的公式： $R_{max}=\left [ \frac{P_{t} G_{t} G_{r} \sigma \lambda ^{2}}{(4\pi)^{3}S_{imin}} \right ]^{1/4}$ 是最基本的雷达方程，它是在理想无损耗、自由空间内传播时的单基地雷达方程。

参数

下面复习一下里面涉及的参数：

发射功率

$P_{t}$ 为雷达发射功率；

天线增益

$G_{t} G_{r}$ 分别是发射天线增益和接收天线增益；

目标的雷达截面积

$\sigma$ 是目标的雷达截面积，用来表征目标散射特性。因为雷达是通过目标的二次散射功率来发现目标的，所以它的值越小就代表目标越难以被发现，从公式给出的关系也能理解这一点。

$\sigma=P_{2}/S_{1}$ ，也就是目标散射的总功率（回来的总数）/照射的功率密度（过去的密度），其中散射总功率也可以写成 $4\pi$ *（返回接收机的每单位立体角的回波功率）。关于立体角可以看看百度给出的标准定义，我理解的立体角是物体投影到以雷达为球心的球面面积除以球体半径的平方，立体角最大值是 $4\pi$ （因为球面面积最大为 $4\pi R^{2}$ ，除以 $R^{2}$ ，就是 $4\pi$ ），也表明 $\sigma=P_{2}/S_{1}$ 分母上是散射回去的总功率。

立体角_百度百科 (baidu.com)https://baike.baidu.com/item/%E7%AB%8B%E4%BD%93%E8%A7%92/7898406从目标的雷达截面积角度讲，任何一个目标都可以想象成一个各向同性的等效球体，即这个等效球体在接收机方向每单位立体角所产生的功率与实际目标每单位立体角散射回接收机功率相等。

波长

$\lambda$ 是发射电磁波的波长，波长和频率成反比；

接收机灵敏度

$S_{imin}$ 是雷达接收机灵敏度，代表着雷达可以探测到的最小的回波信号功率，且 $S_{imin}=kT_{0}BFM$ ， $T_{0}$ 代表温度， $B$ 代表雷达接收机的带宽， $F$ 是噪声系数，它是接收机输入信噪比与输出信噪比的比值， $M$ 是识别系数，代表着接收机输出最小信噪比，也可以用检测因子 $D_{0}$ 来代替。

$D_{0}$ 是在匹配滤波器输出端或检波器输入端要求的单个脉冲的信噪比。 $D_{0}$ 与检测概率和虚警概率有关，它是保证接收机之后的设备可以正常工作的最小信号噪声功率比。

如果我们把 $S_{imin}=kT_{0}BFM$ 带入，那么基本雷达方程就会变成这样： $R_{max}=\left [ \frac{P_{t} G_{t} G_{r} \sigma \lambda ^{2}}{(4\pi)^{3}kT_{0}BFM} \right ]^{1/4}$

单基地雷达的收发天线一般共用，即 $G_{t} G_{r}$ 相等，那么基本雷达方程又变成这样：

$R_{max}=\left [ \frac{P_{t} G_{t} ^{2} \sigma \lambda ^{2}}{(4\pi)^{3}kT_{0}BFM} \right ]^{1/4}$

推导过程

雷达方程来自于”功率“的思想，雷达发射功率为 $P_{t}$ ，如果天线无方向性，即天线方向图是一个各向均匀的球体，球体半径是雷达到目标的距离，那么指向目标方向的功率为 $\frac{P_{t} }{4\pi R^{2}}$ （也就是功率密度），换成有方向的天线后，那么指向目标方向的功率要乘上天线增益（认为是主瓣对准目标） $\frac{P_{t} G_{t}}{4\pi R^{2}}$ ，因为过程是无损耗的，所以认为目标接收到的功率也为 $\frac{P_{t} G_{t}}{4\pi R^{2}}$ ，目标反射的功率要乘上它的雷达截面积 $\sigma$ ，变成 $\frac{P_{t} G_{t}\sigma }{4\pi R^{2}}$ 。还是认为均匀无方向性反射，那么指向雷达方向的功率为 $\frac{P_{t} G_{t}\sigma }{(4\pi R^{2})^{2}}$ ，雷达接收回波信号时也不是全部接收的，这里涉及一个参数：接收天线的有效接收面积 $A_{r}$ ， $A_{r}= \frac{G_{r}\lambda^{2}}{4\pi}$ ，雷达实际接收到的信号功率 $P_{r}$ 就变成最终的 $\frac{P_{t} G_{t}G_{r} \lambda ^{2}\sigma }{(4\pi)^{3} R^{4}}$ .

$S_{imin}$ 代表着雷达可以探测到的最小的回波信号功率，所以在雷达作用范围内的回波信号功率不能小于 $S_{imin}$ ，当 $P_{r}$ 恰好等于 $S_{imin}$ 时，认为公式里面的R是最大作用距离R_{max}。

脉冲积累

观察公式 $R_{max}=\left [ \frac{P_{t} G_{t} ^{2} \sigma \lambda ^{2}}{(4\pi)^{3}kT_{0}BFD_{0}} \right ]^{1/4}$ ，可以发现，如果降低检测因子 $D_{0}$ 的值，雷达的作用距离会增大。那么如何降低 $D_{0}$ 呢？上面我们说，检测因子与发现概率 $P_{d}$ 和虚警概率 $P_{fa}$ 有关，非起伏目标单个脉冲线性检波时 $D_{0}$ 、 $P_{d}$ 和 $P_{fa}$ 具体关系图如下：

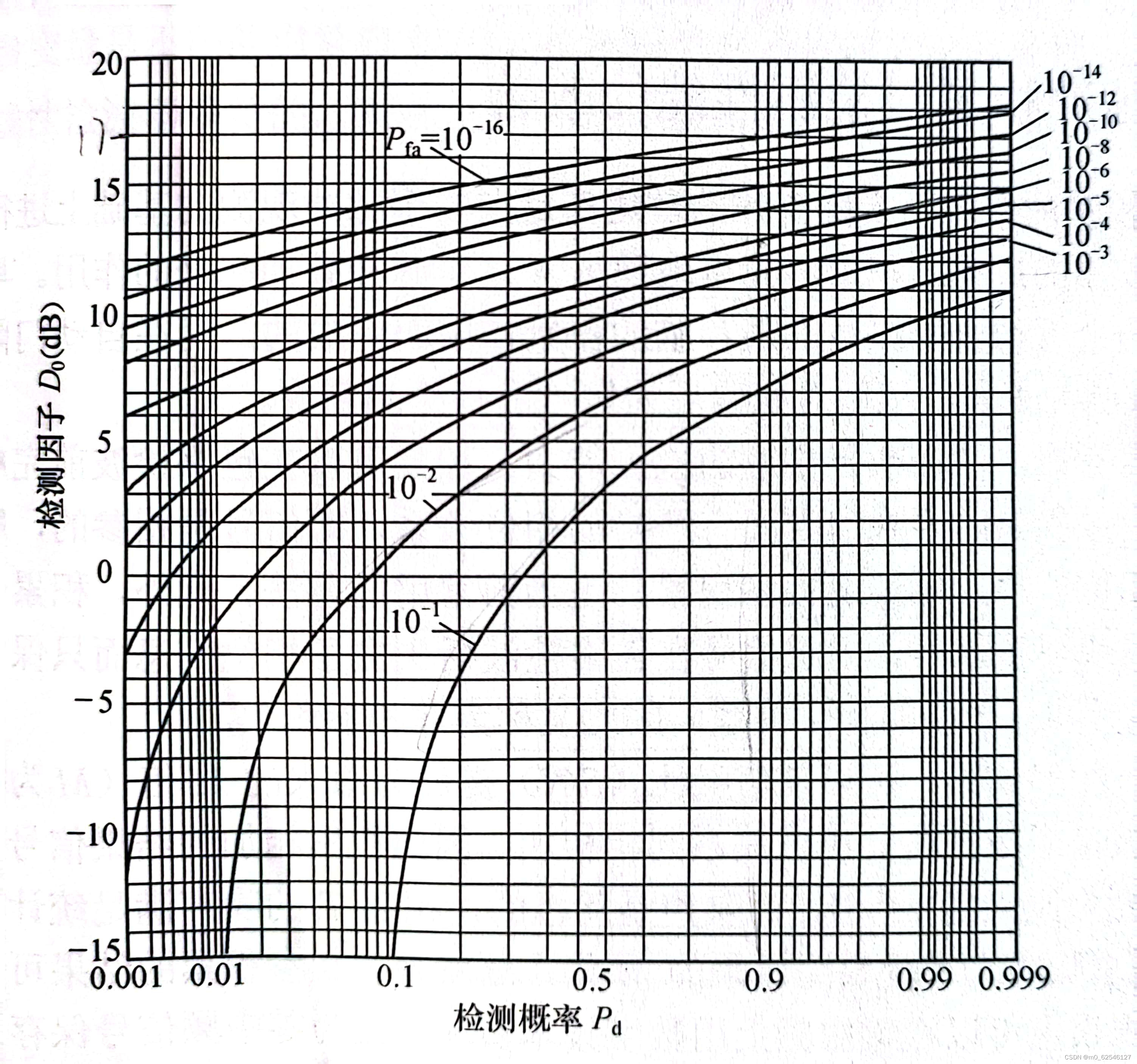
看起来只要降低发现概率（也叫检测概率），提高虚警概率就可以降低检波时所需信噪比（也就是检测因子 $D_{0}$ ），但是如果这么做，雷达的性能会变得很差。这种情况下就需要使用脉冲积累技术。

脉冲积累意味着回波脉冲数不唯一，这是因为雷达天线的波束是不停旋转的，当目标落到3dB范围内认为它可以被发现，所以这部分时间为 $\theta /\omega$ ，而发射脉冲信号的周期为 $T_{r}$ ，频率为 $f_{r}$ ，所以回波个数等于 $\theta *f_{r}/\omega$ 。

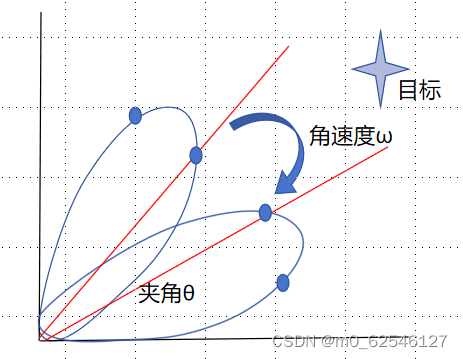
如何理解天线方向图，天线方向图又是如何得出的？ - 知乎 (zhihu.com)https://www.zhihu.com/question/374278666

相参积累

假设有M个脉冲来积累，如果它们的初始相位都相同，那么积累相加后信号振幅为原来的M倍，功率就会变为原来的 $M^{2}$ 倍，而噪声这种随机信号积累后，功率变为原来的M倍，相当于相参积累的输出总信噪比同原来单一脉冲时扩大了M倍。回到 $D_{0}$ 的定义：在匹配滤波器输出端或检波器输入端要求的单个脉冲的信噪比。在总输出信噪比相同的条件下，相参脉冲积累的单个脉冲信噪比要小于不积累的单个脉冲信噪比： $D_{0}(M)=D_{0}(1)/M$ ，带入到雷达方程里，最大作用距离扩大为原来的 $M^{1/4}$ 倍。

相参积累对相位有要求，所以不能放到视频部分积累，此过程放在包络检波前，也称为中频积累。

非相参积累

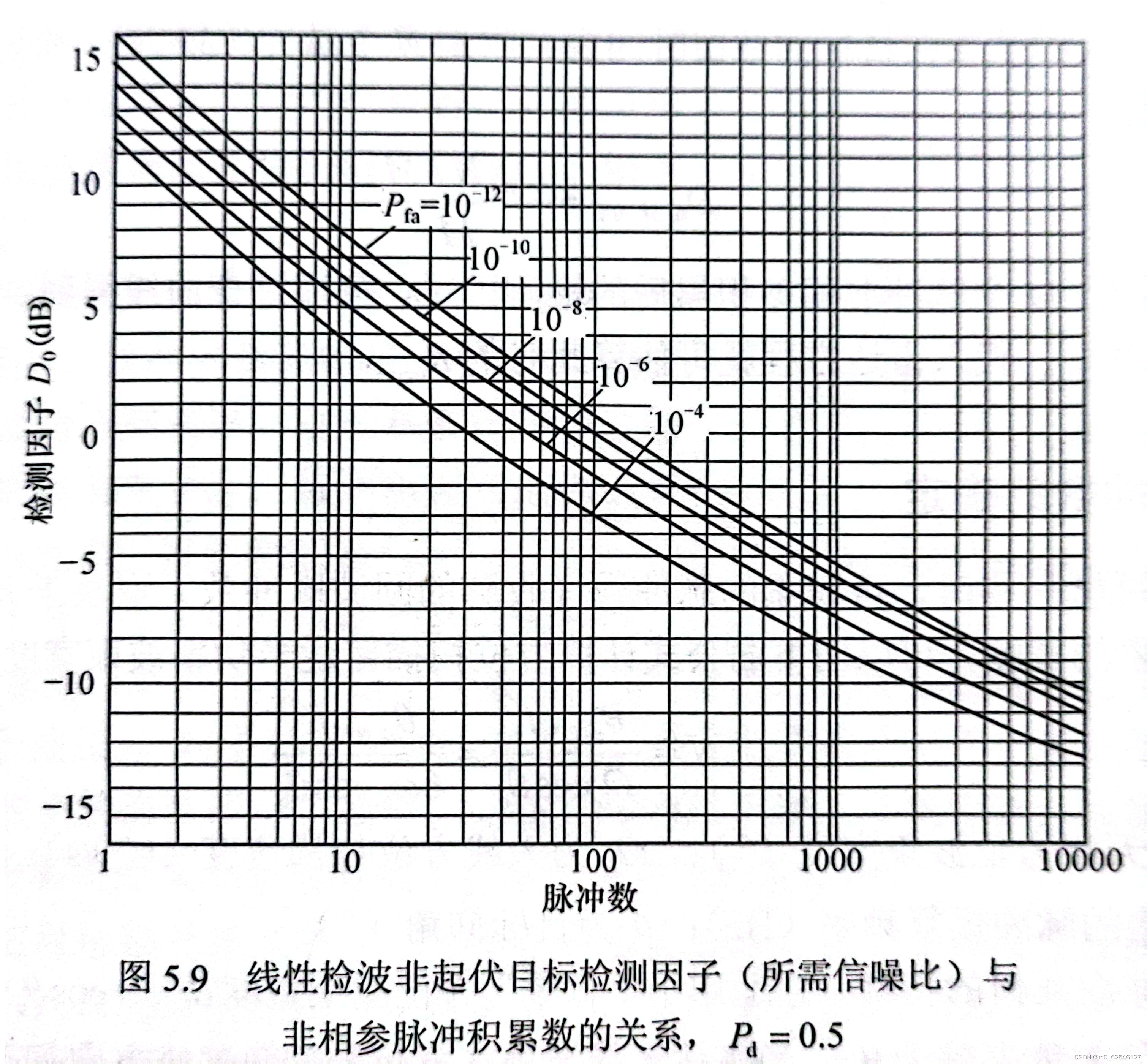
非相参积累意味着M个包络的初始相位不相同，没有严格的相位关系，这个过程是在包络检波后完成的。虽然是把只有幅度信息的M个包络积累起来，但是非相参积累无法达到相参积累对信噪比M倍的放大效果，这是因为检波器的非线性作用增加了信号和噪声的相互作用项，影响输出信噪比。非相参积累的检测因子不容易根据单个脉冲的检测因子计算出来，不过可以给根据脉冲数M、发现概率 $P_{d}$ 和虚警概率 $P_{fa}$ 查图得到：

点目标的雷达截面积

在脉冲雷达中，存在“三维分辨单元”，当目标处在一个分布单元中，雷达会认为这个是一个“点目标”，即不能分辨出一个分辨单元中的多个目标。

当两个回波脉冲靠得很近时，雷达就无法进行分辨，所以在时间上两个信号（回波前沿）至少要相隔 $\tau /2$ ，相应的距离上相距 $\tau c/2$ 。

求出三维立体单元的体积 $\Delta V$ 为 $R\theta _{a}R\theta _{b}\tau c/2$ .当目标的体积小于 $\Delta V$ ，认为这是一个点目标，介绍这部分内容是因为本次介绍是针对点目标的。

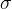$\sigma$ 与波长的关系：

$\lambda > > 2\pi r$ （r为目标等效成的球体的半径）时 $\sigma \propto \lambda ^{-4}$ ，认为处在瑞利区；

$\lambda \approx 2\pi r$ 时 $\sigma$ 在 $\pi r^{2}$ 处起伏，认为处在振荡区； $\lambda < < 2\pi r$ 时 $\sigma$ $\approx$ $\pi r^{2}$ ，认为处在光学区。

$\sigma$ 与极化的关系：

目标的散射特性通常与入射场的极化有关。首先回顾一下极化的内容，电磁场的极化可以分成线极化、圆极化和椭圆极化，其中线极化分为垂直极化，圆极化和椭圆极化又有左旋和右旋之分。任意方向上的线极化都可以分成水平、垂直两个分量。雷达发射什么极化的电磁波就会接收什么极化的电磁波。

线极化

将照射电场分解为 $E_{H}^{T}$ 和 $E_{V}^{T}$ （H代表水平，V代表垂直），将接收电场分解为 $E_{H}^{R}$ 和 $E_{V}^{R}$ ，接收电场和照射电场的关系用矩阵表示为： $\begin{bmatrix} E_{H}^{R}\\ E_{V}^{R}\end{bmatrix}=\begin{bmatrix} \alpha _{HH} &\alpha _{VH} \\ \alpha _{HV} & \alpha _{VV} \end{bmatrix}\begin{bmatrix} E_{H}^{T}\\ E_{V}^{T} \end{bmatrix}$

中间的矩阵称为散射矩阵，它反映目标的散射特性，同时与目标的雷达截面积有关系。

水平极化电磁波照射到同极化的雷达截面积： $\sigma _{HH}=4\pi R^{2}\alpha _{HH}^{2}$ ；水平极化电磁波照射到垂直极化的雷达截面积： $\sigma _{HV}=4\pi R^{2}\alpha _{HV}^{2}$ ；垂直极化电磁波照射到水平极化的雷达截面积： $\sigma _{VH}=4\pi R^{2}\alpha _{VH}^{2}$ ；垂直极化电磁波照射到同极化的雷达截面积： $\sigma _{VV}=4\pi R^{2}\alpha _{VV}^{2}$

圆极化

因为圆极化分左右，所以这里用L代表左旋R代表右旋： $\begin{bmatrix} E_{R}^{S}\\ E_{L}^{S}\end{bmatrix}=\begin{bmatrix} \alpha _{RR} &\alpha _{LR} \\ \alpha _{RL} & \alpha _{LL} \end{bmatrix}\begin{bmatrix} E_{R}^{T}\\ E_{S}^{T} \end{bmatrix}$

有损耗

基本雷达方程里面不考虑这个问题，但是现实中雷达系统里各种各样的损耗会降低最大作用距离，如：失陪损耗、射频传输损耗和天线波束形状损耗等等，我们把它们对最大作用距离的影响用L加在雷达方程的分母中： $R_{max}=\left [ \frac{P_{t} G_{t} ^{2} \sigma \lambda ^{2}}{(4\pi)^{3}kT_{0}BFML} \right ]^{1/4}$ ，L大于1，也可以用分贝值表示。

非自由空间

对于基本雷达方程的第二个约束条件，现实也是不可能达到的。地面（海面）和传播介质对雷达性能的影响集中在三个方面：电波在大气层传播时的衰减；由大气层引起的电波折射；由于反射波和直接波的干涉效应，使天线方向图分裂成波瓣状。

雷达方程的其他形式

(其他形式的最大作用距离)

二次雷达方程

这种形式适用于检测目标上装有应答器的情况，可以理解为目标上也有一个可以发送和接收信号的“小雷达”，这样目标就不再通过散射把信息传递给雷达了，所以这里不会用到 $\sigma$ 。探测过程可以分成两部分：首先，雷达发射电测波到达目标，目标的接收装置接收；然后目标发射信号给雷达，雷达接收天线接收。雷达的基本参数还是那些，目标上的“小雷达”的基本参数用对应的加撇的量表示。

先看第一部分，雷达发目标收，目标接收功率为 $P_{t}{}'=$ $\frac{P_{t} G_{t}G_{r} \lambda ^{2} }{(4\pi)^{3} R_{1}^{4}}$ ，令目标能接收的最小功率为 $S{}'_{imin}$ ，那么这里的最大作用距离为 $R_{1max}=\left [ \frac{P_{t} G_{t} G{}'_{r}\lambda ^{2}}{(4\pi)^{3}S{}'_{imin}} \right ]^{1/4}$ 。再看第二部分，目标发雷达收，雷达接收功率为 $P_{t}=$ $\frac{P{}'_{t} G{}'_{t}G_{r} \lambda ^{2} }{(4\pi)^{3} R_{2}^{4}}$ ，令雷达能接收的最小功率为 $S_{imin}$ ，求出这里的最大作用距离为 $R_{2max}=\left [ \frac{P{}'_{t} G{}'_{t} G_{r}\lambda ^{2}}{(4\pi)^{3}S_{imin}} \right ]^{1/4}$ .整体上二次雷达的最大作用距离是取 $R_{1max}$ 和 $R_{2max}$ 的最小值。这里的天线增益也可以根据之前提到的公式换成有效接受面积A。

双基地雷达方程

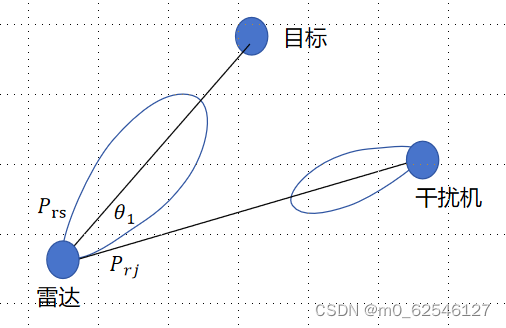
基本雷达方程条件里的第三条是“单基地”，可以理解为发射机和接收机在同一空间点，那么双基地就是接收和发送在两个不同的位置。这种情况下收发天线不能共用。

通过上面的示意图应该很好理解“双基地”的概念。接收天线接收到的功率为 $P_{t}=$ $\frac{P_{t} G_{t}G_{r} \lambda ^{2}\sigma }{(4\pi)^{3} R_{t}^{2}R_{r}^{2}}$ 。需要注意两点：第一，要研究的作用距离分成发射 $R_{t}$ 和接收 $R_{r}$ 两部分，它们不能合并；第二，这里的目标的雷达截面积 $\sigma$ 和之前都不太一样，因为入射和反射角度不同，需要记住“目标的雷达截面积 $\sigma$ 与自身性质和角度都有关，它反映物体的散射性质”。令雷达能接收的最小功率为 $S_{imin}$ ，那么可以求出 $(R_{t}R_{r})_{max}=\left [ \frac{P_{t} G_{t} G_{r}\sigma \lambda ^{2}}{(4\pi)^{3}S_{imin}} \right ]^{1/2}$ 。由于发射天线、目标和接收天线三点构成三角形，所以 $R_b$ 、 $R_t$ 和 $R_r$ 满足三角形三边关系： $R_{t}+R_{r}\geq R_{b}$ ， $R_{t}-R_{r}\leq R_{b}$ .

由于截面积的特性，双基地雷达可以用于“反隐身”，但是存在“波速追赶”的问题，即发射天线波束和接收天线波束要对准目标，下面给出“对不准”的情况示意图。

波束对不准目标影响会公式里的天线增益， $G_{t}$ 变为 $G_{t}F(\theta _{1})$ ， $G_{r}$ 变为 $G_{r}F(\theta _{2})$ 。 $F(\theta )$ 是功率归一化天线方向图函数，也可以用电压归一化天线方向图函数，不过要加平方。天线方向图函数主要给出主瓣内非最大增益方向的增益与最大值的关系，这是前面没介绍的，补一个坑。

用能量信号表示的雷达方程

还是回到基本雷达方程 $R_{max}=\left [ \frac{P_{t} G_{t} ^{2} \sigma \lambda ^{2}}{(4\pi)^{3}kT_{0}BFM} \right ]^{1/4}$ ，它用到了雷达发射功率 $P_{t}$ ，可以认为这是一种用功率表示的形式。 $P_{t}$ 是峰值功率。

如果在接收机部分使用匹配滤波器，那么接收机带宽和脉冲宽度之间有这样的关系： $B=1/\tau$ (抱歉，这还是前面留下的坑)，把分母上的B替换掉，分子上出现 $P_{t}\tau$ ，根据峰值功率的定义，很容易看出它是能量E，再考虑上适配损失，能量表示的雷达方程为 $R_{max}=\left [ \frac{E G_{t} ^{2} \sigma \lambda ^{2}}{(4\pi)^{3}kT_{0}FMC_{B}} \right ]^{1/4}$ 。使用能量方便分析包络不规则的雷达脉冲信号。

干扰环境

之前介绍过噪声、干扰和杂波的定义，但是在分析雷达方程时没有考虑过这一方面的影响，现在讨论一下。通过能否自己发射电磁波给干扰分为有源干扰和无源干扰。没有考虑干扰之前，我们都是通过最小能接受到的功率来推算最大作用距离，考虑干扰后需要通过信噪比（或信干比）的门限来计算。

有源干扰

雷达接收目标散射回来的功率为 $P_{rs}=$ $\frac{P_{t} G_{t}G_{r} \lambda ^{2}\sigma }{(4\pi)^{3} R^{4}L}$ ,接收到干扰信号的功率为 $P_{rj}=$ $\frac{P_{j} G_{j}G_{r}{}' \lambda ^{2} \Delta f_{j} }{(4\pi)^{2} R_{j}^{2}L\Delta f_{r}}$ . $P_{rj}$ 的公式里有三个要点需要解释：第一， $G_{r}{}'$ 不是最大的增益，这是因为雷达的最大增益要对准目标，干扰机和目标不在同一个方向；第二，之前没有出现过的 $\Delta f_{r} \Delta f_{j}$ 分别是接收机带宽和干扰信号带宽，在干扰之前需要对雷达进行“侦擦”，得到其射频信号的中心频率和带宽，如果没有这部分信息只是发任意频率信号干扰的话，干扰信号大概率无法通过射频滤波进入中频放大器，一般让干扰信号的中心频率对齐射频载波频率，其带宽稍大于雷达信号带宽，这样射频滤波后保留的 $\Delta f_{r}$ 内都有干扰信号存在；第三，这里雷达接收没有再除以 $4\pi R^{2}$ ，目前我还没弄懂原因，希望有大佬能指点一二。

令信干比的门限为A， $P_{rs}/P_{rj}=A$ ，求出最大作用距离。

无源干扰

不能发出电磁波进行干扰，所以这里利用的是散射波，比如在飞机周围撒开箔条丝可以对雷达进行干扰。不同于有源干扰，这里的干扰源和目标可以认为在同一位置。

雷达接收目标散射回来的功率为 $P_{rs}=$ $\frac{P_{t} G_{t}G_{r} \lambda ^{2}\sigma }{(4\pi)^{3} R^{4}}$ ,接收到杂波信号的功率为 $P_{rc}=$ $\frac{P_{t} G_{t}G_{r} \lambda ^{2}\sigma_{c} }{(4\pi)^{3} R^{4}}$ . $P_{rc}$ 的公式里有一个要点需要解释： $\sigma_{c}$ 是箔条丝的雷达截面积，如果箔条丝没有多到互相遮挡，那么 $\sigma_{c}=N\sigma_{d}*0.5c\tau R^{2}\theta_{\alpha }\theta_{\beta } /V_{c}$ ，它的涵义是箔条总数*单根箔条的雷达截面积*三维立体单元的体积/箔条分布空间体积。设这里的信号与杂功率比为 $S_{0}/C_{0}$ ， $P_{rs}/P_{rc}=$ $S_{0}/C_{0}$ ，求出最大作用距离。