三维信息的表征形式

参考B站up主“飞船12138”的系列视频

一、点云

点云是一种由大量三维空间中的点组成的数据集，每个点包含位置信息（通常是X、Y、Z坐标）以及可能的其他属性，如颜色、法线向量、反射强度等。点云数据通常通过激光扫描仪（LiDAR）、结构光扫描仪、立体视觉相机或RGB-D相机等设备获取。

点云的深度学习方法在近年来发展迅速，包括点云的标定、融合、自动分类、显示和后处理应用等内容。点云深度学习的任务主要集中在分类、分割、目标检测、实例分割、配准和重构等方面。根据数据输入和网络结构，点云深度学习方法主要分为多视图、基于点、基于体素以及混合方法。

点云的获取方式通常包括激光扫描、摄影测量、雷达等。点云数据的特点是稀疏性、无序性和不规则性，这些特点使得点云处理面临挑战，如需要对输入点的顺序不敏感，以及处理不规则分布的数据。

在三维重建中，点云扮演着至关重要的角色，可以精确地重建出物体的三维形状，不仅有助于定量分析和测量，还可用于逆向工程、文物保护等领域。例如，在建筑领域，通过对古建筑进行三维扫描和重建，可以获取其精确的几何形状和尺寸信息，为保护和修复工作提供支持。

二、参数化曲线曲面

参数化曲线曲面是一种在计算机图形学和相关领域中表达和处理三维几何形状的重要技术。它涉及将复杂的三维形状映射到二维平面上，以便进行更高效的计算和处理。

参数表示

参数化曲线和曲面通常通过参数方程来表示。

对于曲线，这可能是形式为 P(t)=[x(t),y(t)] 的二维表示，或者对于三维空间曲线，形式为 P(t)=[x(t),y(t),z(t)]。

对于曲面，参数化可能表示为 p(u,v)=p(x(u,v),y(u,v),z(u,v))，其中(u,v) 是在[0,1]×[0,1] 范围内的参数 。

参数方程的优势

参数方程提供了多种优势，包括满足几何不变性的要求、更大的自由度来控制形状、直接对参数方程进行几何变换、便于处理斜率为无穷大的情形、简单的范围界定、以及易于使用向量和矩阵运算来简化计算 。

参数化的应用

参数化技术在计算机图形学中有广泛的应用，包括纹理映射、曲面拟合、曲面对应、重新网格化、曲面编辑、形状变形、形状分析等 。

参数化的方法

参数化的方法包括固定边界方法和自由边界方法。这些方法通过不同的数学技术，如优化、几何变换和数值方法，来实现曲面到平面的映射 。

参数化的度量

在参数化过程中，保持几何性质的度量是一个重要考虑因素。这包括角度、面积、距离等的保持。雅可比矩阵在度量局部形变时起到关键作用 。

参数化曲面的基本概念

参数化曲面可以表示为 r=r(u,v)=(x(u,v),y(u,v),z(u,v))r=r(u,v)=(x(u,v),y(u,v),z(u,v))。这种表示方法允许对曲面进行局部和全局的分析，包括切向量、法向量、曲率和挠率的计算 。

参数化曲线：

参数化曲面：

三、隐式曲线曲面

隐式曲线曲面是一种在计算机图形学中常用的表示三维形状的方法。它通过一个或多个方程隐式地定义曲线或曲面，而不是直接列出构成曲线或曲面的点。

定义：平面上的隐式曲线由方程  F(x,y)=0 给出，空间中的隐式曲面由方程 F(x, y, z)=0 定义。这些方程隐式地描述了曲线或曲面上所有点的集合。

梯度和法向量：
   在隐式曲面上，梯度向量  F 与曲面垂直，因此可以用来计算曲面的法向量。梯度的大小与曲率有关，这在计算光线与曲面的交互时非常有用。

几何不变量和连续性：
   隐式曲线曲面的几何不变量包括曲率公式。在隐式曲线曲面中，可以研究至少二阶几何连续性问题，例如切线连续（G1连续）和曲率连续（G2连续）。

绘制算法：
   隐式曲线曲面的绘制算法可能涉及区间算术，以提高绘制的精确度和速度。这些算法通常需要解决额外零水平集的问题，并降低计算成本。

   隐式曲线曲面的优点在于它们的形式简单，易于判断点与曲面的关系，适合执行几何运算，如布尔运算（并集、交集、差集）等。
   隐式曲面不适合直接采样曲面上的点，且难以显式构造位于曲面上的点。
   隐式曲线曲面在计算机图形学中有广泛的应用，包括但不限于建模、渲染、光线追踪和物理模拟。它们特别适合于表示光滑曲面和复杂形状，如毛发和光滑的有机表面。

   与参数化曲线曲面相比，隐式曲线曲面不需要对数据点进行参数化，这使得它们在处理复杂几何形状时更为灵活。

隐式曲面可以进一步分类为代数曲面、Constructive Solid Geometry（CSG）、符号距离函数（Signed Distance Function）、水平集（Level Set）和分型几何（Fractals）等。

隐式曲线曲面提供了一种强大且灵活的方式来表示和处理三维几何形状，但是它们在采样和显式构造方面存在一些挑战。
 

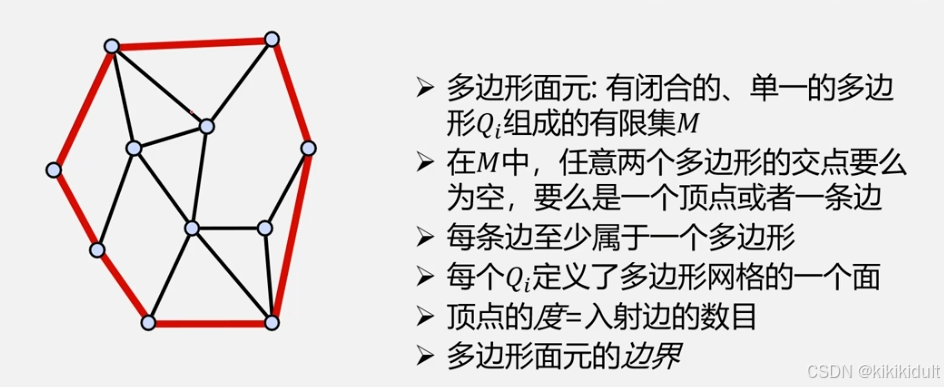
四、多边形面元

多边形面元是计算机图形学中用于表示三维几何体表面的基本元素。在三维建模和渲染中，复杂的三维形状通常由多个多边形（如三角形或四边形）组成，这些多边形相互连接，形成网格，从而定义了物体的表面。

定义：多边形面元是由若干个平面多边形围成的几何体的面。这些多边形可以是三角形、四边形或其他多边形，它们在顶点处相连，形成封闭的表面。多边形面元的集合定义了物体的形状和结构。

应用：

多边形面元在计算机图形学中有广泛的应用，包括三维建模、渲染、动画和游戏开发。它们是构建和处理三维几何形状的基础，可以用于创建逼真的视觉效果和物理模拟。

数据结构：

在计算机图形学中，多边形面元通常通过数据结构如顶点列表、边列表和面列表来表示。这些数据结构存储了构成多边形面元的顶点、边和面的几何信息，以及它们之间的拓扑关系。

细分和平滑：

多边形面元可以通过细分算法如Catmull-Clark细分来增加表面细节，从而创建更平滑的曲面。这种细分过程通过在原始多边形基础上增加新的顶点和面来实现，使得几何体表面更加细腻和光滑。

渲染：

在渲染过程中，多边形面元被用来计算物体的光照、阴影和纹理映射。渲染引擎会处理多边形面元的顶点数据，计算每个面的法向量，以及应用纹理和颜色，以生成最终的图像。

实体和表面：多边形面元可以构成实体或表面。实体是指形成封闭空间区域的多边形网格，而表面则不形成封闭区域，表示一个无限薄的曲面。

文件格式：

多边形面元数据通常存储在特定的文件格式中，如Wavefront OBJ、STL、PLY等，这些格式定义了如何表示多边形面元的几何和拓扑信息。

处理和操作：

在图形软件和编程库中，多边形面元可以进行各种操作，如添加、删除、分割和合并。这些操作允许用户对三维模型进行编辑和优化。

多边形面元是计算机图形学中表示和处理三维形状的基本构建块，它们为创建和操作复杂的三维几何体提供了强大的工具和方法。
 

多边形面元：

三角形面元：

Bowyer-Waston算法：SDF+三角剖分

五、体素

体素（Voxel）是三维空间中的最小单位，类似于二维图像中的像素（Pixel）。体素可以被视为一个立方体，每个体素包含一个值及其三维位置，这个值可以是灰度值、颜色值或其他物理量。体素的数量与图像尺寸的立方成正比，因为它是由分辨率和图像尺寸共同决定的。

体素在计算机图形学中的应用非常广泛，它们可以用于表示三维物体的体积数据，这使得体素非常适合于体积渲染和存储复杂的几何形状。体素数据结构通常用于医学成像、三维建模、地质勘探等领域。在医学成像中，体素可以用来表示身体的不同组织，每个体素的值可以代表组织的密度或其它相关的医学信息。

体素与点云（Point Cloud）不同，点云是三维坐标空间中的点集合，通常由3D扫描仪捕获。每个点可能包含颜色、法线和其他属性。点云提供了一种更为直接和轻量级的方式来表示三维空间，但数据不连续，可能需要复杂的后处理步骤。

在虚拟地理环境构建中，体素可以用来模拟三维地形和自然现象、表达地理过程以及进行基于地理环境的空间分析。体素模型能够提供连续的空间表示，易于进行体积渲染和计算，但缺点是数据量大，需要更多的存储空间和计算资源。

体素是三维图形学中的一种基础数据结构，它通过在三维空间中划分体积单元来表示和处理三维数据。体素的使用为三维建模、渲染和分析提供了强大的工具，尤其是在需要精确控制体积数据的领域。