【3D应力敏感度分析拓扑优化】【基于p-范数全局应力衡量的3D敏感度分析】基于伴随方法的有限元分析和p-范数应力敏感度分析（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、文章下载

---

💥1 概述

摘要
本文用于三维基于应力的敏感度分析。包括基于伴随方法的有限元分析和p-范数应力敏感度分析。详细介绍了基于p-范数全局应力衡量的3D敏感度分析。通过与有限差分逼近的比较，验证了分析敏感度的正确性。非线性优化求解器选择了移动渐近线法（MMA）。为验证敏感度分析代码的有效性，提出了三个典型的体积约束应力最小化问题。本文可以扩展到解决不同与应力有关的3D拓扑优化问题。

随着计算资源和先进制造技术的提高，拓扑优化（Topology Optimization, TO）等结构优化工具在设计过程中的作用越发重要。TO最早由Bendsoe和Kikuchi于1988年提出，用于确定代表几何结构中材料分布的设计变量的理想值，通常为刚度。优化后的刚度设计可制造出在工业应用中吸引人的复杂、有机和轻量化的设计。然而，这些设计容易产生应力集中，可能导致设计在使用中出现问题。因此，在工业应用中，必须将应力约束包括在TO中，以确保最佳设计满足所有工程要求，且不会大幅偏离最初优化的结果。正如Le等人在2010年指出的，实施应力约束面临三大挑战："奇异"现象（Duysinx和Bendsøe 1998）、应力作为局部结果以及应力的非线性。

许多论文讨论了奇异现象（Guo等，2011；Paris等，2010；Cheng和Guo，1997；Kirsch，1990；Luo等，2013；Xia等，2012，2018；Zhang等，2013；Fan等，2019；Deng等，2020a, 2019, 2020b；Deng和To，2020），即低密度设计变量仍具有应变值，导致人为生成的应力值过大，复杂化优化过程。为解决这一挑战，人们开发了不同的方法。Cheng和Guo（1997）采用应变放松方法缓解这些低密度元素中的应变。Bruggi（2012）、Le等人（2010）和Holmberg（2013）对基于密度变量的应力进行惩罚。这三个研究都使用了固体各向同性材料加惩罚（SIMP）方法，将每个密度变量表示为1到0之间的连续值。Xia等人（2018）通过使用双向进化结构优化（BESO）方法避免了奇异性问题。BESO方法将每个变量离散表示为1或0，代表实体或空白材料，消除了中间值和中间值带来的奇异性。据指出，另一种TO方法——水平集方法也解决了受应力约束的TO问题（Guo等，2011；Xia等，2012, 2014；Zhang等，2013；Wang和Li，2013；Allaire和Jouve，2008；Suresh和Takalloozadeh，2013；James等，2012；Miegroet和Duysinx，2007；Allaire等，2014；Picelli等，2018a, 2018b；Emmendoerfer和Fancello，2016；Kambampati等，2020；Song等，2020；Yang等，2018）。水平集方法也像BESO一样离散表示材料，并且避免了奇异现象。其他关于应力相关拓扑优化的先进方法可以在文献中找到（Zhang等，2017, 2016, 2018；Cai和Zhang，2015）。然而，本文将着重介绍基于应力的拓扑优化中SIMP方法的实施。第二个挑战在于应力是在每个元素上局部计算的。正如Duysinx和Bendsoe（Duysinx和Bendsøe，1998）所述，这就需要为每个元素设置一个约束，并增加计算问题所需的计算资源。相比之下，Dusyinx和Sigmund（Duysinx和Sigmund，1998）引入了全局应力约束，将所有局部应力归为一种度量。然而，全局约束不能很好地控制局部应力行为。因此，Paris等人（2009）、Le等人（2010）和Holmberg等人（2013）提出了区域方法。这些方法根据附近元素或按照排序后的应力值分组元素约束。研究发现，区域方法是一个令人满意的折衷方案，可以限制约束的数量，同时仍然提供良好的局部应力控制。第三个挑战在于应力的非线性行为。元素应力的测量受到了该元素局部邻域中密度的极大影响。因此，Le等人（2010）使用密度变量滤波器来平滑密度变量和敏感度，通过对相邻节点进行加权平均，消除了先前拓扑优化算法中的棋盘效应，产生了平滑设计，并更好地收敛到全局最小值。

详细文章见第4部分。

📚2 运行结果

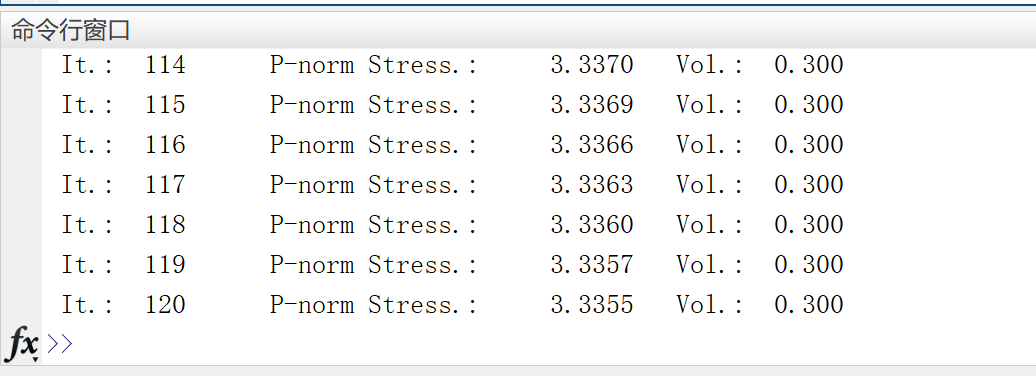
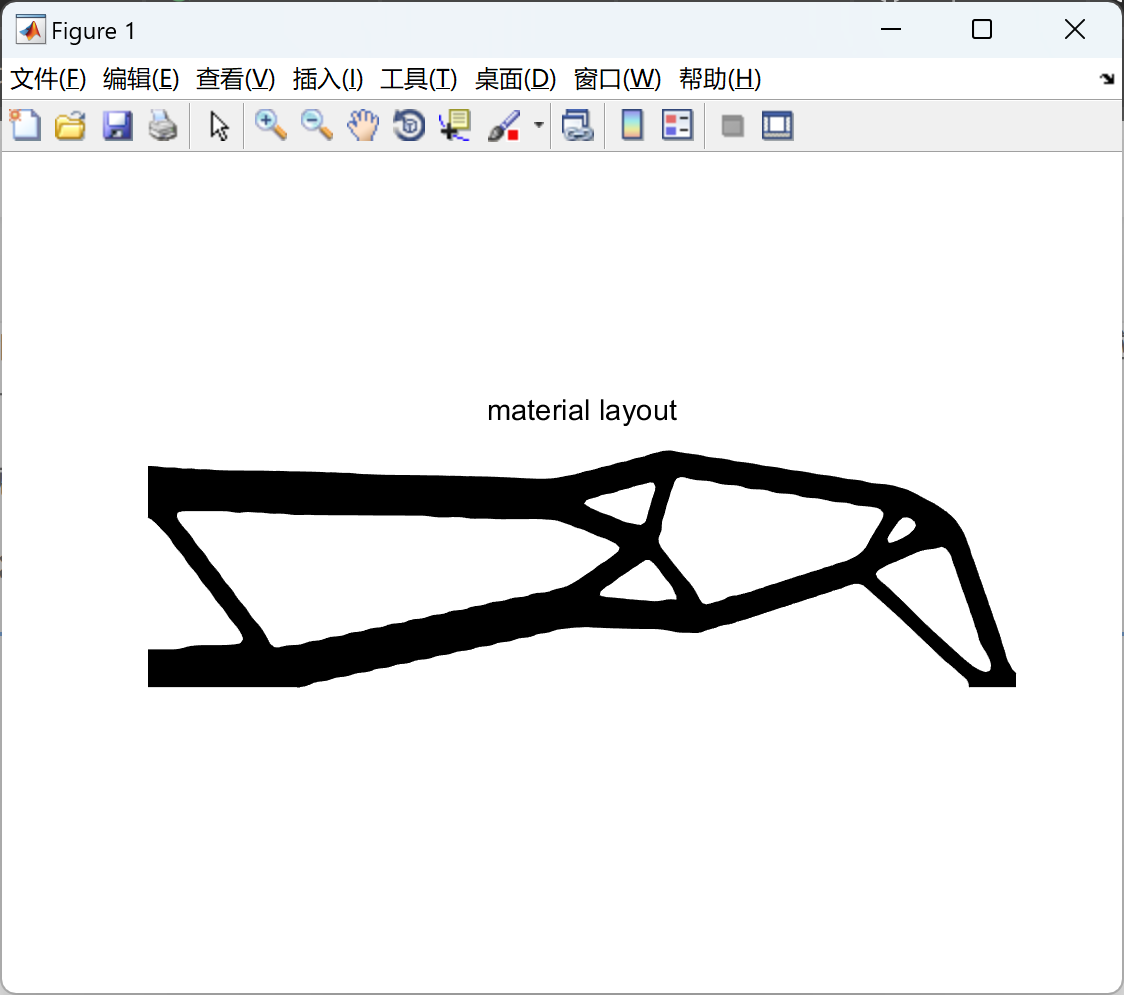
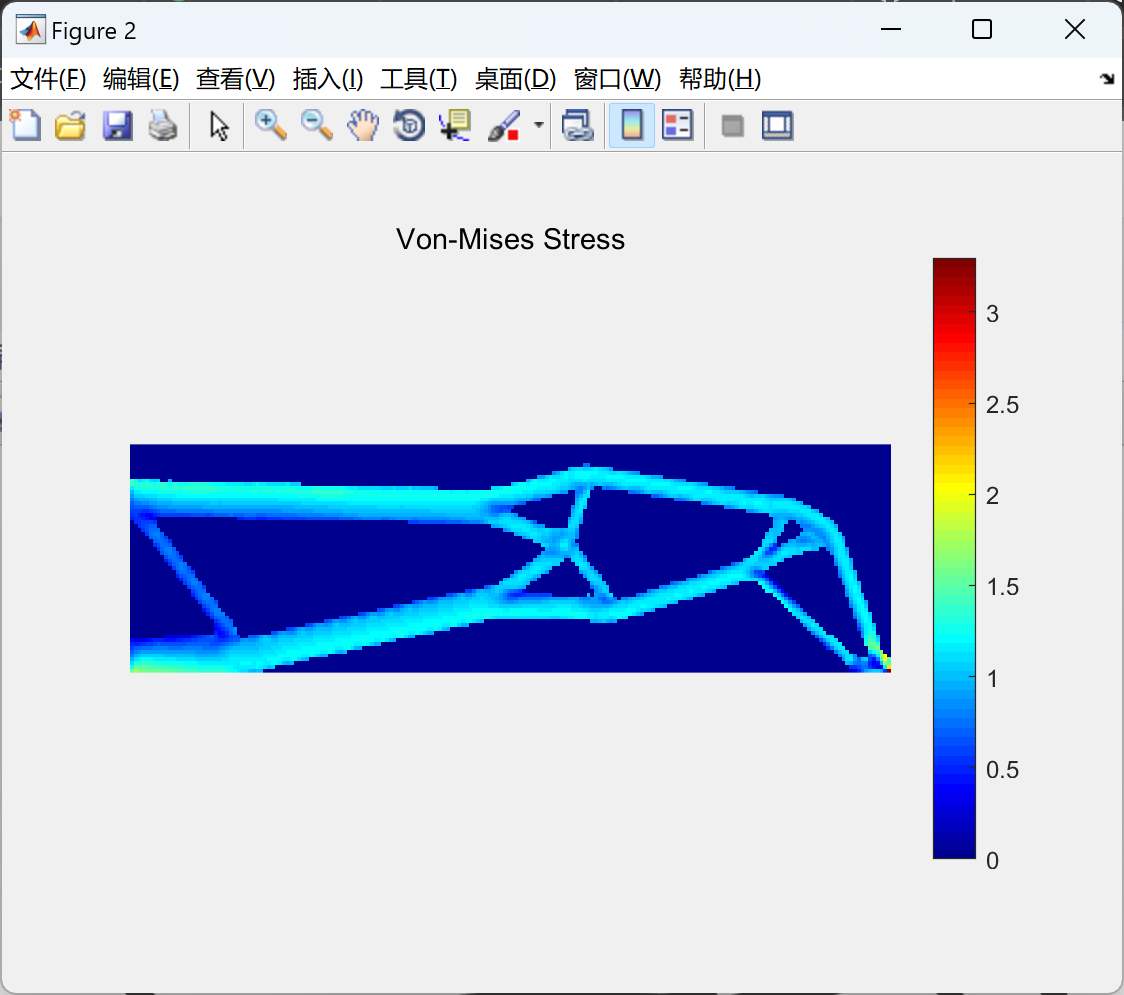
部分代码：

function[residu,residunorm,residumax] = ...
kktcheck(m,n,x,y,z,lam,xsi,eta,mu,zet,s, ...
         xmin,xmax,df0dx,fval,dfdx,a0,a,c,d);
%
%  The left hand sides of the KKT conditions for the following
%  nonlinear programming problem are calculated.
%         
%      Minimize  f_0(x) + a_0*z + sum( c_i*y_i + 0.5*d_i*(y_i)^2 )
%    subject to  f_i(x) - a_i*z - y_i <= 0,  i = 1,...,m
%                xmax_j <= x_j <= xmin_j,    j = 1,...,n
%                z >= 0,   y_i >= 0,         i = 1,...,m
%*** INPUT:
%
%   m    = The number of general constraints.
%   n    = The number of variables x_j.
%   x    = Current values of the n variables x_j.
%   y    = Current values of the m variables y_i.
%   z    = Current value of the single variable z.
%  lam   = Lagrange multipliers for the m general constraints.
%  xsi   = Lagrange multipliers for the n constraints xmin_j - x_j <= 0.
%  eta   = Lagrange multipliers for the n constraints x_j - xmax_j <= 0.
%   mu   = Lagrange multipliers for the m constraints -y_i <= 0.
%  zet   = Lagrange multiplier for the single constraint -z <= 0.
%   s    = Slack variables for the m general constraints.
%  xmin  = Lower bounds for the variables x_j.
%  xmax  = Upper bounds for the variables x_j.
%  df0dx = Vector with the derivatives of the objective function f_0
%          with respect to the variables x_j, calculated at x.
%  fval  = Vector with the values of the constraint functions f_i,
%          calculated at x.
%  dfdx  = (m x n)-matrix with the derivatives of the constraint functions
%          f_i with respect to the variables x_j, calculated at x.
%          dfdx(i,j) = the derivative of f_i with respect to x_j.
%   a0   = The constants a_0 in the term a_0*z.
%   a    = Vector with the constants a_i in the terms a_i*z.
%   c    = Vector with the constants c_i in the terms c_i*y_i.
%   d    = Vector with the constants d_i in the terms 0.5*d_i*(y_i)^2.
%     
%*** OUTPUT:
%
% residu     = the residual vector for the KKT conditions.
% residunorm = sqrt(residu'*residu).
% residumax  = max(abs(residu)).
%
rex   = df0dx + dfdx'*lam - xsi + eta;
rey   = c + d.*y - mu - lam;
rez   = a0 - zet - a'*lam;
relam = fval - a*z - y + s;
rexsi = xsi.*(x-xmin);
reeta = eta.*(xmax-x);
remu  = mu.*y;
rezet = zet*z;
res   = lam.*s;
%

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

🌈4 Matlab代码、文章下载