初步了解:
Foc其实就是控制三相逆变电路,通过六个mos的通断来控制三相电流通断及方向

三相电流的三相坐标系如下:通过磁场的叠加来吸引转子旋转,所以我们可以对三相电流的大小以及方向进行控制,产生大方向大小不同的磁场,来带动转子旋转。

但是直接控制三相的交流电流太困难了,为了方便控制电机,我们将这三相电流通过clark和park转换成旋转坐标系下的dq轴,d轴是电机的轴向方向,q轴是电机的切向方向,通过给定不同的q轴电压,可以形成不同的q轴电流,使得电机运动。dq轴是与电机同步旋转的,从而我们可以直观的控制q轴来控制电机,不用去跟踪控制复杂的三相正弦波。

路径1:根据给定目标电压 输出三项占空比
Uq,Ud-->revpark->svpwm->CCR1,2,3
Revpark 将旋转坐标系下的dq轴,分解转换到静止坐标系αβ轴
α= (d * cosTheta - q * sinTheta);
β= (d * sinTheta + q * cosTheta);

通过控制逆变电路的六个mos,是可以产生六个矢量(U1,U2,U3,U4,U5,U6),但是如何更精细的对每个角度进行控制呢,这就要用到矢量合成了,通过两个附近的易形成的矢量(mos的六个状态)来合成目标的矢量即可。如图中的红色矢量就要通过U4,U6来合成。

为了简化步骤,可以直接将αβ的分量转换到到六个定矢量中的两个上,省略掉αβ这两个矢量合成目标矢量这个过程,但是如何来判断应该具体转换到哪两个上就要通过扇区判断了。
扇区判断:根据求得的αβ的大小以及正负,来得知这个目标矢量所在扇区
计算机语言化即判断这个几个量的正负即可:
alpha beta tan30 * beta - alpha
Alpha和beta都是正的,就可以锁定在第一象限了,那么如何来确定是在Ⅰ扇区还是Ⅱ扇区呢? 这个时候也就要用到第三个判别量了
假设目标矢量刚好在U6边界线上时,可以求出以β为基准的α的大小,再与实际的α作比较来得出这个目标矢量是在30度的区间还是六十度的区间。如果假设的的大于实际的,目标矢量则在Ⅰ扇区,反之假设小于实际的,目标矢量则在Ⅱ扇区。上图中tan30 * beta - alpha肯定是小于0的,所以是在Ⅰ扇区
现在已知在哪两个矢量之间了,只要求出两个矢量的作用时长比例即可确定目标矢量的方向了
Svpwm:求出目标矢量的边界矢量作用时间以及空矢量作用时间(空矢量时长,决定这个目标矢量大小)
根据图形关系,将α,β分解到U6,U4上可以求出两个边界矢量的大小
U6= β/(cosΠ/6) =T1+T6
U4= α+ β/(sinΠ/6) =T2+T5
如果最开始vq和vd的矢量和是1的话,那么这个时候U6和U4加起来也是1
但是在大多数情况下都不会满幅输出,所以算出来的U6和U4之和也不是1,所以还会有时间使得空矢量存在(空矢量也就是上管全开或者下管全开)
t空=(1-tu6-tu4)。
已知时间之后,我们要做的就是将这个时长比例作用到逆变电路上了,采用到的是中心对齐模式的pwm,每对互补通道去控制一对mos,互补通道也可以防止上下管同时导通,正负极直接短路,改变ccr来改变每个矢量开断的时间。
那么为什么要采用中心对齐呢:我们希望能尽量减少MOS管的开关次数,以最大限度减少开关损耗,所以采用七段式SVPWM调制法,在每个状态切换的时候,只有一对mos发生了变化000->100->110->111->110->100->000,一个周期跑完之后再去更新下一阶段的ccr值。在这一个周期内,每相的变化都是0->1->0。

最后转化到三相ccr也就是图中蓝线和红线的交点,代码为:
CCRS1 = (tA * (foc.ARR);
CCRS2 = (tB * (foc.ARR));
CCRS3 = (tC * (foc.ARR));
路径二:三相电流重构 Ia,Ib,Ic->clark->park->Iq,Id
将方便跟踪的曲线转换为直线变换
-
Clark
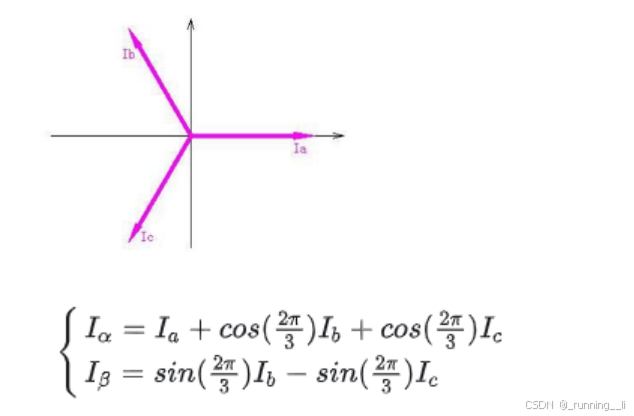
由于这样推导出来Iα等于3/2Ia,为了更直观计算,所以要进行等幅值变换,也就是在等号右边乘以2/3 如下为矩阵形式

2,Park
将αβ轴转化到dq轴

得到dq电流之后,便可以进行电流闭环了,电流环框架基本完成
代码整体运行流程以及框架:
上电电压检测成功后
a,进行adc校准,0位偏移补偿,以及各种外设初始化,开启双线程
b,进行编码器校准,对齐电角度和机械角度,一个线程跑vd强拖,另一个线程记录编码器角度偏移量,
c,进入闭环,一个线程进行通信方向的数据处理,另一个线程跑电机控制,包括电流采样及重构,角度获取,三环pid计算,svpwm的输出
本文为个人理解,方便记录,借鉴了一些图片和文章,如有不对请指出,可以交流。
























 1554
1554

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








