图网络 MixHop 简介

1 模型提出

标题：MixHop: Higher-Order Graph Convolutional Architectures via Sparsified Neighborhood Mixing
链接：https://arxiv.org/abs/1905.00067

标准GCN只能学习到相邻结点之间的信息，不能学习邻里混合关系。

为了解决这个缺点，作者提出了一个新的模型，MixHop，通过重复混合不同距离的邻居的特征表示，它可以学习这些关系，包括不同的运算子。MixHop不需要额外的内存或计算复杂性，并且在具有挑战性的基线上表现优异。

此外，作者提出稀疏正则化，使我们可以可视化网络如何优先考虑不同图数据集的邻域信息。

对学习的体系结构的分析表明，邻域混合随着数据集的不同而不同。

MixHop 的三个假设

• H1:： MixHop模型学习delta运算符。
• H2：在真正的半监督学习任务中，使用邻域混合的高阶图卷积可以比现有方法(例如标准GCNs)表现更好。
• H3：学习MixHop的模型架构时，每个图的最佳性能架构是不同的。

2 模型结构

高阶信息的传递

在信息传递过程中，节点从它们的直接节点(一级)邻居接收潜在的表示，并进一步从远距离的N度邻居中接收信息。

作者据此将在不同距离获取的邻居信息进行混合。

邻居信息混合的方式

Delta Operator：是一个从不同距离收集的节点特征之间的减法操作。普通的GCN无法学习这样的特性表示。

Two-hop Delta Operator 的定义如下：

这样的运算子允许模型表示邻居之间的特征差异，可以学习到图的边界情况。例如，要了解有一个受欢迎的德国朋友的美国人大致特征，可能最直接的朋友说英语，但很多朋友的朋友说德语。这个美国人可以通过学习对比英语和德语的one-hop和two-hop语言的卷积过滤器来表示。

上述定义不允许学习 two-hop Delta算子的直接形式，而允许学习它的一个变换，只要这个变换可以是倒置的(即 $f$ 是内射的)。

为此，作者采用下式作为上述定义的替换(GC layer)：

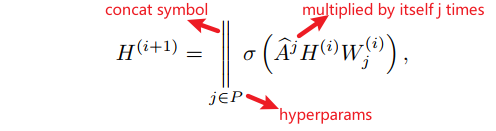
不用计算${\hat{A}}^j$，而是采用由右向左的方式计算，如：

$$\hat{A}\left(\hat{A}\left(\hat{A}{H}^{(i)}\right)\right),j=3$$

对于邻接矩阵${\hat{A}}^j$采用稀疏矩阵的存储方式。

上述GC layer可用下图表示：

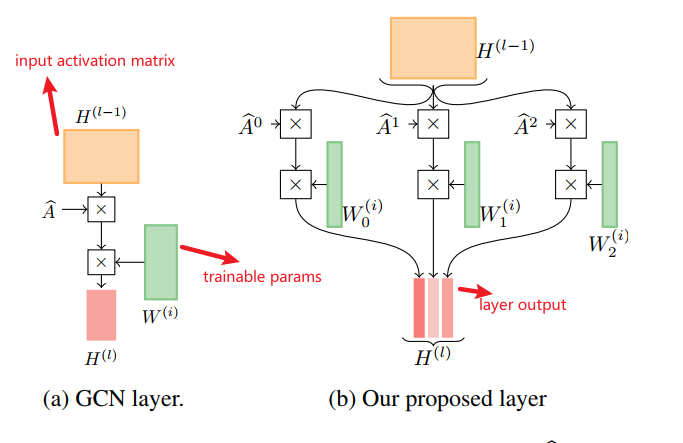
证明GC layer能够代表Two-hop Delta Operator

H ( 1 ) = ∥ j ∈ { 0 , 1 , 2 } σ ( A ^ j X W j ( 0 ) ) = σ ( ∑ j ∈ { 0 , 1 , 2 } ∥ A j ^ X W j ( 0 ) ) = σ ( [ I N X W 0 ( 0 ) ; A ^ X W 1 ( 0 ) : A ^ 2 X W 2 ( 0 ) ] ) \begin{aligned} H^{(1)}=& \|_{j \in\{0,1,2\}} \sigma\left(\widehat{A}^{j} X W_{j}^{(0)}\right) \\ =& \sigma\left(\sum_{j \in\{0,1,2\}}^{\|} \widehat{A^{j}} X W_{j}^{(0)}\right) \\ =& \sigma\left(\left[I_{N} X W_{0}^{(0)} ; \widehat{A} X W_{1}^{(0)}: \widehat{A}^{2} X W_{2}^{(0)}\right]\right) \end{aligned} H(1)===​∥j∈{0,1,2}​σ(A jXWj(0)​)σ⎝⎛​j∈{0,1,2}∑∥​Aj XWj(0)​⎠⎞​σ([IN​XW0(0)​;A XW1(0)​:A 2XW2(0)​])​

令$W_0^{(0)}=0(\text{zero matrix})$ ，$W_1^{(0)}=W_2^{(0)}=I_{s_0}$，则上式可以简化为：

$$H^{(1)}=\sigma \left(\left[\begin{array}{lll}0& \hat{A}X& {\hat{A}}^{2}X\end{array}\right]\right)$$

特征向量 $H^{(1)}$ 可以嵌入第二层：

$$H^{(2)}=\left[\begin{array}{ccc}{I}_N{H}^{(1)}{W}_0^{(1)}& \hat{A}{H}^{(1)}{W}_1^{(1)}& {\hat{A}}^2{H}^{(1)}{W}_2^{(1)}\end{array}\right]$$

令$W_1^{(1)}=W_2^{(1)}=0$ 以及

$$W_0^{(1)}=\left[\begin{array}{c}0\\ I_{s_0}\\ -I_{s_0}\end{array}\right]$$

则：

$$H^{(2)}=\left[\left(\sigma (\hat{A}X)-\sigma \left({\hat{A}}^{2}X\right)\right):0:0\right]$$

这说明我们的GCN可以根据定义成功地表示two-hop Delta算子。

对上面的two-hop Delta算子进行泛化：

$$f\left(\sum _{j=0}^m{\alpha }_j\sigma \left({\hat{A}}^{j}X\right)\right)$$

则$W_0^{(1)}$可以泛化为：

$$W_0^{(1)}=\left[\begin{array}{c}{\alpha }_0{I}_{s_0}\\ ⋮\\ {\alpha }_m{I}_{s_0}\end{array}\right]$$

3 学习邻接矩阵幂结构

具体来说，分阶段训练架构：

1. 构建一个宽的网络(例如，邻接矩阵宽度为200)，只在深度上做选择。
2. 在每个$W_j(l)$的每一列上应用 L2 Group Lasso 正则化来训练任务中的网络。这将使整个列的值(接近)降为零。
3. 在峰值验证精度处，测量每个$W_j(l)$的 L2 范数。选择一个阈值，并计算每个$W_j(l)$中 norm 高于该阈值的列数。在实验中，作者选择了使收缩模型的大小等于我们的基线模型的大小(即 P = { 1 } P = \{1\} P={1})的阈值。
4. 通过删除规范低于第 k 个百分位数的列来收缩权重矩阵。
5. 用 L2正则化 替换 L2组套索。重新训练。

4 实验

• 在合成数据上取得的效果

• 在真实数据上取得的效果

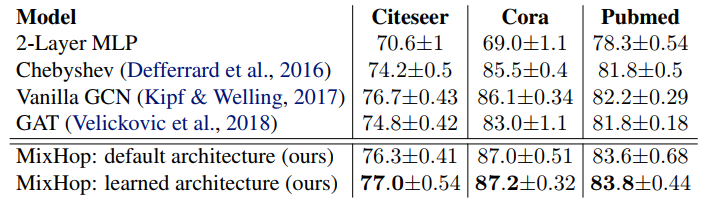
• 不同数据学得的不同结构

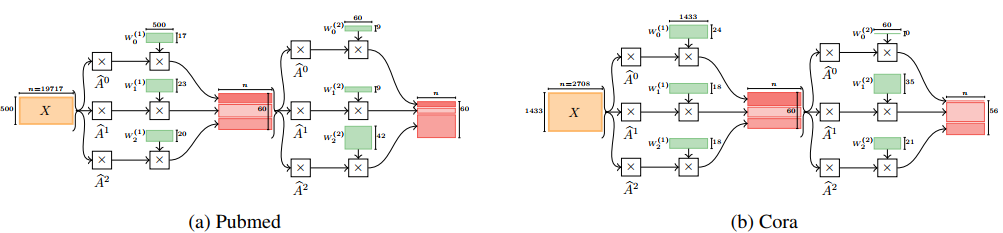
具体实现见：

https://github.com/benedekrozemberczki/MixHop-and-N-GCN