Mujoco 学习系列（九）官方教程 The LQR tutorial synthesizes a linear-quadratic controller, balancing a humanoid

班长我是读书人

已于 2025-05-28 11:54:40 修改

阅读量741

点赞数 15

CC 4.0 BY-SA版权

分类专栏： Mujoco 文章标签：学习

于 2025-05-27 20:41:03 首次发布

本文链接：https://blog.csdn.net/nenchoumi3119/article/details/148263549

Mujoco 专栏收录该内容

12 篇文章

订阅专栏

这篇文章是追随 Mujoco Github 仓库中官方教程的第三篇 《The LQR tutorial synthesizes a linear-quadratic controller, balancing a humanoid on one leg》，涉及到一些最优控制的内容。

官方 Github 仓库：https://github.com/google-deepmind/mujoco
官方 Colab 链接：https://colab.research.google.com/github/google-deepmind/mujoco/blob/main/python/LQR.ipynb#scrollTo=Xqo7pyX-n72M

在这里插入图片描述

官方和我自己的博客代码放在下面的链接中，所有以 [offical] 开头的文件都是官方笔记，所有以 [note] 开头的文件都是和博客对应的笔记：

链接: https://pan.baidu.com/s/1mFtyCtog0iVN_hrAIFoYFQ?pwd=83a4 提取码: 83a4

1. 导入必要的包

import distutils.util
import os
import subprocess

import mujoco
import numpy as np
from typing import Callable, Optional, Union, List
import scipy.linalg

import mediapy as media
import matplotlib.pyplot as plt

np.set_printoptions(precision=3, suppress=True, linewidth=100)

from IPython.display import clear_output
clear_output()

2. 加载并渲染基础模型

这一步需要将 mujoco 官方仓库下载下来并放到当前目录下：

(mujoco) $ git clone https://github.com/google-deepmind/mujoco

此时你的文件结构如下：

(mujoco) $ tree -L 1

├── demo.ipynb
└── mujoco		# 官方Github仓库

加载模型：

with open('mujoco/model/humanoid/humanoid.xml', 'r') as f:
  xml = f.read()
  
model = mujoco.MjModel.from_xml_string(xml)
data = mujoco.MjData(model)
renderer = mujoco.Renderer(model)

使用前向动力学推动一帧渲染

mujoco.mj_forward(model, data)
renderer.update_scene(data)
media.show_image(renderer.render())

在这里插入图片描述

该模型自带一些内置的“关键帧”，用于保存模拟状态，可以使用 mj_resetDataKeyframe 进行加载：

for key in range(model.nkey):
    mujoco.mj_resetDataKeyframe(model, data, key)
    mujoco.mj_forward(model, data)
    renderer.update_scene(data)
    media.show_image(renderer.render())

在这里插入图片描述

仿真并生成一段视频：

DURATION = 3
FRAMERATE = 60

mujoco.mj_resetDataKeyframe(model, data, 1)
frames = []

while data.time < DURATION:
    mujoco.mj_step(model, data)
    if len(frames) < data.time * FRAMERATE:
        renderer.update_scene(data)
        pixels = renderer.render()
        frames.append(pixels)
        
media.show_video(frames, fps=FRAMERATE)

在这里插入图片描述

该模型定义了内置扭矩执行器，可以通过设置 data.ctrl 向量来驱动人形机器人的关节。下面的代码使用一个自定义摄像头来追踪人形机器人的质心，并向运动控制中注入噪声。

DURATION = 3
FRAMERATE = 60

camera = mujoco.MjvCamera()
mujoco.mjv_defaultFreeCamera(model, camera)
camera.distance = 2

mujoco.mj_resetDataKeyframe(model, data, 1)

frames = []
while data.time < DURATION:
    data.ctrl = np.random.randn(model.nu)
    mujoco.mj_step(model, data)
    
    if len(frames) < data.time * FRAMERATE:
        camera.lookat - data.body('torso').subtree_com
        renderer.update_scene(data, camera)
        pixels = renderer.render()
        frames.append(pixels)
        
media.show_video(frames)

在这里插入图片描述

3. 单腿稳定站立

官方文档在这里花了一些篇幅介绍最优化控制的知识点，但这不是该系列博客的重点，故在此处不详细展开，感兴趣的可以前往原始文档阅读，或看下面这张图：

在这里插入图片描述

3.1 使用逆运动学计算控制点

mujoco 的正向动力学函数 mj_forward计算给定状态和系统所有力的加速度；逆动力学函数将加速度作为输入，并计算产生加速度所需的力。mujoco 的 快速逆动力学 考虑了所有约束，包括接触约束。

将在期望的位置设定点处调用正向动力学函数，将 data.qacc 中的加速度设置为 0，然后调用逆动力学函数：

mujoco.mj_resetDataKeyframe(model, data, 1)
mujoco.mj_forward(model, data)

data.qacc = 0
mujoco.mj_inverse(model, data)
print(data.qfrc_inverse)

在这里插入图片描述

检查逆动力学的输出发现在根关节的垂直运动自由度上施加了一个非常大的力。这意味着，为了解释关于加速度为零的要求，逆动力学必须发明一种直接施加于根关节的力。

当以 $\mu$ 为增量，将人形机器人上下移动 1 毫米时，这个力是如何变化的：

height_offsets = np.linspace(-0.001, 0.001, 2001)
vertical_forces = []

for offset in height_offsets:
    mujoco.mj_resetDataKeyframe(model, data, 1)
    mujoco.mj_forward(model, data)
    data.qacc = 0
    
    data.qpos[2] += offset
    mujoco.mj_inverse(model, data)
    vertical_forces.append(data.qfrc_inverse[2])

找到在垂直自由度上施加最小力的 height-offset：

idx = np.argmin(np.abs(vertical_forces))
best_offset = height_offsets[idx]
print(best_offset)

绘制曲线

plt.figure(figsize=(10, 6))
plt.plot(height_offsets * 1000, vertical_forces, linewidth=3)
plt.axvline(x=best_offset*1000, color='red', linestyle='--')
weight = model.body_subtreemass[1]*np.linalg.norm(model.opt.gravity)
plt.axhline(y=weight, color='green', linestyle='--')
plt.xlabel('Height offset (mm)')
plt.ylabel('Vertical force (N)')
plt.grid(which='major', color='#DDDDDD', linewidth=0.8)
plt.grid(which='minor', color='#EEEEEE', linestyle=':', linewidth=0.5)
plt.minorticks_on()
plt.title(f'Smallest vertical force '
          f'found at offset {best_offset*1000:.4f}mm.')
plt.show()

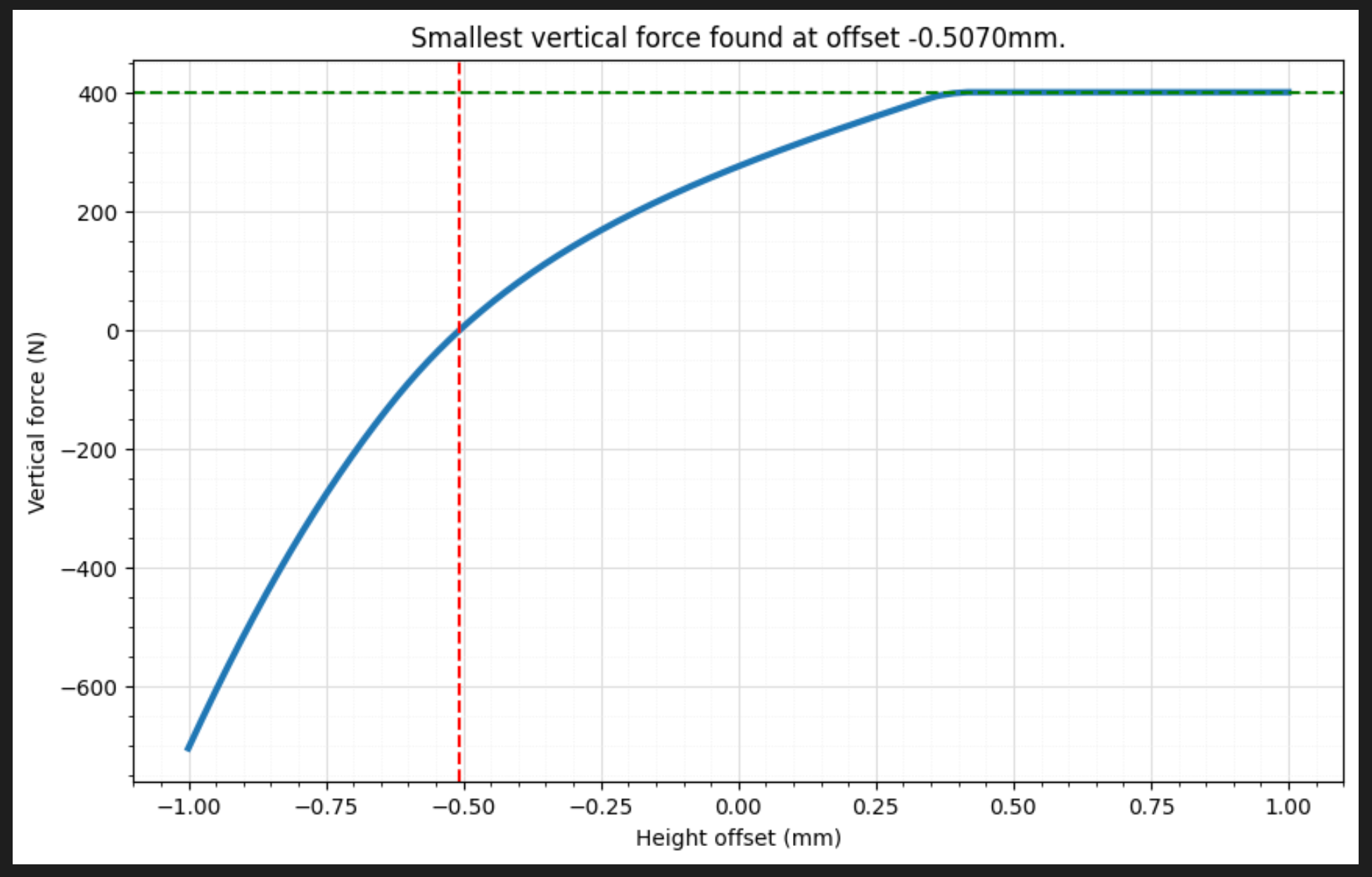
在这里插入图片描述

在上图中可以看到由于脚部接触而产生的强烈非线性关系：

图像左侧：当机器人推向地面时，有一个很大的外力将其下压；
图像右侧：当机器人移离地面时，有一个力将其拉伸，脚不再接触地面的高度，所需的力恰好等于人形机器人的重量（绿线），并且在继续向上移动时保持不变；
接近 -0.5 毫米是理想的高度偏移（红线），此时垂直加速度为零可以完全由内部关节力提供，而无需借助外力。

校正初始姿势的高度，将其保存在 qpos0 中，然后再次计算逆动力学力：

mujoco.mj_resetDataKeyframe(model, data, 1)
mujoco.mj_forward(model, data)

data.qacc = 0
data.qpos[2] += best_offset
qpos0 = data.qpos.copy()
mujoco.mj_inverse(model, data)
qfrc0 = data.qfrc_inverse.copy()

print('desired forces:', qfrc0)

在这里插入图片描述

输出显示根关节上的力很小。既然执行器能够合理产生的力，那么如何找到能够产生这些力的执行器值。对于人形机器人这样的简单电机执行器，可以简单地“除”以驱动力矩臂矩阵，即乘以其伪逆：

actuator_moment = np.zeros((model.nu, model.nv))
mujoco.mju_sparse2dense(
    actuator_moment,
    data.actuator_moment.reshape(-1),
    data.moment_rownnz,
    data.moment_rowadr,
    data.moment_colind.reshape(-1),
)
ctrl0 = np.atleast_2d(qfrc0) @ np.linalg.pinv(actuator_moment)
ctrl0 = ctrl0.flatten()
print('control setpoint:', ctrl0)

在这里插入图片描述

在正向动力学中应用这些控制，并将它们产生的力与上面打印的期望力进行比较：

data.ctrl = ctrl0
mujoco.mj_forward(model, data)
print('actuator forces:', data.qfrc_actuator)

在这里插入图片描述

由于人形机器人已完全驱动（除根关节外），且所需的力均在执行器的限制范围内，因此可以看到所有内部关节的力与期望力完美匹配。根关节仍然存在一些不匹配的情况，但幅度很小，应用这些控制后模拟的效果：

DURATION = 3
FRAMERATE = 60

mujoco.mj_resetDataKeyframe(model, data, 1)
data.qpos = qpos0
data.ctrl = ctrl0

frames = []
while data.time < DURATION:
    mujoco.mj_step(model, data)
    if len(frames) < data.time * FRAMERATE:
        camera.lookat = data.body('torso').subtree_com
        renderer.update_scene(data, camera)
        pixels = renderer.render()
        frames.append(pixels)
        
media.show_video(frames)

在这里插入图片描述

与先前直接倒地的视频相比，可以看到这是一个更好的控制设定点。虽然机器人仍然会摔倒，但它会尝试稳定下来，并在较短的时间内维持住平衡。

3.2 选择 Q 和 R 矩阵

为了得到LQR反馈控制律，需要设计𝑄和𝑅矩阵。由于其线性结构，解对两个矩阵的缩放具有不变性，因此在不失一般性的情况下，可以选择 $R$ 作为单位矩阵：

nu = model.nu
R = np.eye(nu)

选择 $Q$ 矩阵更为复杂，将它构造为两个项的和：

首先平衡成本将使重心 (CoM) 保持在脚部上方，将使用运动雅可比矩阵，它映射关节空间和全局笛卡尔位置；

nv = model.nv
mujoco.mj_resetData(model, data)
data.qpos = qpos0
mujoco.mj_forward(model, data)
jac_com = np.zeros((3, nv))
mujoco.mj_jacSubtreeCom(model, data, jac_com, model.body('torso').id)

jac_foot = np.zeros((3, nv))
mujoco.mj_jacBodyCom(model, data, jac_foot, None, model.body('foot_left').id)

jac_diff = jac_com - jac_foot
Qbalance = jac_diff.T @ jac_diff

其次，关节偏离其初始配置的代价需要为不同的关节组设置不同的系数：

自由关节的系数为 0，因为它已由 CoM 成本项处理；
左腿保持平衡所需的关节，即左腿关节和水平腹部关节，应保持与其初始值相当接近；
所有其他关节的系数都应较小，以便人形机器人能够挥动手臂来保持平衡；

获取所有这些关节组的索引：

joint_names = [model.joint(i).name for i in range(model.njnt)]

root_dofs = range(6)
body_dofs = range(6, nv)
abdomen_dofs = [
    model.joint(name).dofadr[0]
    for name in joint_names
    if 'abdomen' in name
    and not 'z' in name
]
left_leg_dofs = [
    model.joint(name).dofadr[0]
    for name in joint_names
    if 'left' in name
    and ('hip' in name or 'knee' in name or 'ankle' in name)
    and not 'z' in name
]

balance_dofs = abdomen_dofs + left_leg_dofs
other_dofs = np.setdiff1d(body_dofs, balance_dofs)

现在可以构建 Q 矩阵了，但要注意平衡项的系数需要相当高。这有三个原因：

这是最关心的目标，平衡意味着保持重心 (CoM) 位于足部上方；
对重心 (CoM) 的控制权较小（相对于身体关节而言）；
在平衡状态下，长度单位“更大”。如果膝盖弯曲 0.1 弧度（≈6°），仍然可能恢复，但如果重心位置距离足部位置偏向 10 厘米，就很可能已经落地了。

# 常数系数
BALANCE_COST        = 1000
BALANCE_JOINT_COST  = 3
OTHER_JOINT_COST    = 0.3

# 构造 Qjoint 矩阵
Qjoint = np.eye(nv)
Qjoint[root_dofs, root_dofs] *= 0
Qjoint[balance_dofs, balance_dofs] *= BALANCE_JOINT_COST
Qjoint[other_dofs, other_dofs] *= OTHER_JOINT_COST

Qpos = BALANCE_COST * Qbalance + Qjoint

Q = np.block([[Qpos, np.zeros((nv, nv))],
              [np.zeros((nv, 2*nv))]])

3.3 计算 LQR 增益矩阵 K

在求解 LQR 控制器之前，还需要 𝐴 和 𝐵 矩阵。这些矩阵由 mujoco 的 mjd_transitionFD 函数计算，该函数使用高效的有限差分导数来计算它们，并利用可配置的计算流水线来避免重新计算未发生变化的量。

mujoco.mj_resetData(model, data)
data.ctrl = ctrl0
data.qpos = qpos0

A = np.zeros((2*nv, 2*nv))
B = np.zeros((2*nv, nu))
epsilon = 1e-6
flg_centered = True
mujoco.mjd_transitionFD(model, data, epsilon, flg_centered, A, B, None, None)

现在可以开始求解稳定控制器了，使用 scipy 的 solve_discrete_are 函数来求解 Riccati 方程，并根据概述中描述的公式得到反馈增益矩阵。

# 求解 Riccati 方程.
P = scipy.linalg.solve_discrete_are(A, B, Q, R)

# 计算增益矩阵 K.
K = np.linalg.inv(R + B.T @ P @ B) @ B.T @ P @ A

3.4 稳定站立

现在可以尝试稳定控制器了。为了应用增益矩阵𝐾，需要使用 mj_differentiatePos 来计算两个位置的差值，因为根方向由一个长度为 4 的四元数给出，而两个四元数的差值（在切线空间中）的长度为 3。在 mujoco 中，位置 (qpos) 的大小为 nq，而位置差值（和速度）的大小为 nv。

DURATION = 5 
FRAMERATE = 60 

mujoco.mj_resetData(model, data)
data.qpos = qpos0

dq = np.zeros(model.nv)

frames = []
while data.time < DURATION:
  mujoco.mj_differentiatePos(model, dq, 1, qpos0, data.qpos)
  dx = np.hstack((dq, data.qvel)).T

  # LQR control law.
  data.ctrl = ctrl0 - K @ dx

  mujoco.mj_step(model, data)
  if len(frames) < data.time * FRAMERATE:
    renderer.update_scene(data)
    pixels = renderer.render()
    frames.append(pixels)

media.show_video(frames, fps=FRAMERATE)

在这里插入图片描述

3.5 完整视频

上面的视频中人形机器人基本上是静止的，为了更符合实际情况，对代码进行如下修改：

在 LQR 控制器上注入平滑的噪声，使平衡动作更加明显；
在场景中添加接触力可视化；
使摄像机围绕人形机器人平滑旋转；
实例化一个分辨率更高的新渲染器；

DURATION = 12  
FRAMERATE = 60
TOTAL_ROTATION = 15   # degrees
CTRL_RATE = 0.8
BALANCE_STD = 0.01 
OTHER_STD = 0.08

camera = mujoco.MjvCamera()
mujoco.mjv_defaultFreeCamera(model, camera)
camera.distance = 2.3

scene_option = mujoco.MjvOption()
scene_option.flags[mujoco.mjtVisFlag.mjVIS_CONTACTFORCE] = True

model.vis.map.force = 0.01

定义两个辅助函数：

def unit_smooth(normalised_time: float) -> float:
  return 1 - np.cos(normalised_time*2*np.pi)
def azimuth(time: float) -> float:
  return 100 + unit_smooth(data.time/DURATION) * TOTAL_ROTATION

执行仿真：

np.random.seed(1)
nsteps = int(np.ceil(DURATION/model.opt.timestep))
perturb = np.random.randn(nsteps, nu)

CTRL_STD = np.empty(nu)
for i in range(nu):
  joint = model.actuator(i).trnid[0]
  dof = model.joint(joint).dofadr[0]
  CTRL_STD[i] = BALANCE_STD if dof in balance_dofs else OTHER_STD

# 对噪声进行平滑
width = int(nsteps * CTRL_RATE/DURATION)
kernel = np.exp(-0.5*np.linspace(-3, 3, width)**2)
kernel /= np.linalg.norm(kernel)
for i in range(nu):
  perturb[:, i] = np.convolve(perturb[:, i], kernel, mode='same')

mujoco.mj_resetData(model, data)
data.qpos = qpos0

renderer = mujoco.Renderer(model, width=1280, height=720)

frames = []
step = 0
while data.time < DURATION:
  mujoco.mj_differentiatePos(model, dq, 1, qpos0, data.qpos)
  dx = np.hstack((dq, data.qvel)).T

  # LQR control law.
  data.ctrl = ctrl0 - K @ dx

  data.ctrl += CTRL_STD * perturb[step]
  step += 1

  mujoco.mj_step(model, data)

  if len(frames) < data.time * FRAMERATE:
    camera.azimuth = azimuth(data.time)
    renderer.update_scene(data, camera, scene_option)
    pixels = renderer.render()
    frames.append(pixels)

media.show_video(frames, fps=FRAMERATE)

在这里插入图片描述