一、PMSM 电机参数介绍
1.1 转子极数
转子极数 (Rotor Poles) :三相交流电机每组线圈都会产生 N、S 磁极,每个电机每相含有的永磁体磁极个数就是极数。由于磁极是成对出现的,所以电机有 2、4、6、8……极 (偶数)。
未知参数的电机,可以通过快速的将转子转动一周,观察示波器上出现线电压峰值出现的次数即为电机的极数。也可以用另一个电机以已知的转速拖动待测电机来得到极数。
1.2 定子电阻
定子电阻 (Stator Resistance) 是指电枢内部 (定子线圈) 的电阻,一般指相电阻 (单位为:Ω)。可以通过对未知参数的电机测试得到三种组合 (U-V,V-W,W-U) 的线电阻值,电机线电阳之和后除 2得到。
1.3 DQ 轴电感
永磁同步电机根据永磁体的安装方式不同可分为两类:
表贴式永磁同步电机 (SM-PMSM) 和嵌入式永磁同步电机 (IPMSM)。
1.3.1 表贴式永磁同步电机 (SM - PMSM)
表贴式电机 (SM - PMSM),也叫隐极电机,本身具有各向同性的结构,即直轴和交轴 (Ld 和 Lq) 是相同的。通常情况下,其机械结构产生更广泛的气隙,这反过来又意味着弱磁能力更低。
1.3.2 嵌入式永磁同步电机 (IPMSM)
内转子式电机 (IPMSM),也叫凸极电机,显示出各向异性结构 (LdㄑLq) 这一特殊的磁场结构可以用来产生更大的电磁转矩。具有优良的机械结构,通常气隙很狭窄,从而弱磁能力更好。
1.3.3 鉴别 SM-PMSM 和 IPMSM 电机
将电机从电路中断开,用电感表接在电机的线一线端,非常地缓慢转动电机转子 (要防止感应电压对测量的影响),如果电感表示数的最大值最小值差别不大 (小于 10%),说明该电机为表面磁钢永磁电机 (SPM),此时可以将两个值取平均即为电机相电感 (L=Lq=Ld);否则为内嵌磁钢永磁电机(IPM),且电感表测得数值的最大值为 2 倍的 Lq,最小值为 2 倍的 Ld (对于 Y 形接法的电机来说,电感表测得的数据是两相绕组串连的电感)。
1.3.4 SM-PMSM 和 IPMSM 电机结构差异
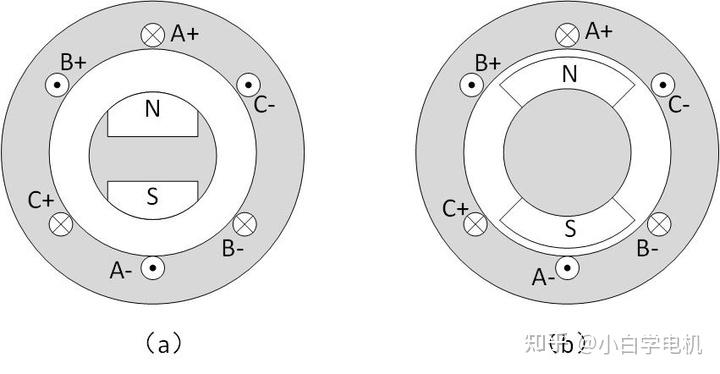
电机的 d 轴和 q 轴是一个很重要的概念,他们是相对于转子而言的。对于电机来说,d 轴即转子磁钢磁极所在轴线,方向是从 S 极指向 N 极。q 轴与 d 轴垂直,方向逆时针沿 d 轴转过 90 度。说是凸极隐极,其实是根据 d 轴和 q 轴的同步电感来确定的。
图 (a) 是内嵌式永磁同步电机,即凸极永磁同步电机:
内嵌式永磁同步电机里头d轴方向的用铁量比较少,因为除了空气气隙,还有永磁体占用了一定空间。永磁体磁导率相当于空气,而铁的导磁率约为 200~400 Ur 。 q 轴除了空气气隙就是铁了,用铁量比 d 轴要多,所以 d 轴电感小,q 轴电感大。
图 (b) 是表贴式永磁同步电机,即隐极永磁同步电机:
而隐极的磁铁是在气隙里头的,d 轴方向和 q 轴方向用铁量一样多,所以 d 轴和 q 轴的电感相等。
其中磁路 IPMSM 磁路如下:

1.3.5 电机的凸级效应
SM-PMSM 相当于是 dq 轴磁导率相同,而 IPMSM 的 dq 轴磁导率不同。这种磁路不对称性称为凸极效应,凸极率定义为 IPMSM 的
,而表贴式电机(SPMSM)因气隙均匀
。
1.4 转矩常数
电动机所产生转矩的比例系数,一般表示每安培电枢电流所能产生的转矩大小,单位 nm/A。
1.5 反电动势系数
电动机旋转时,电枢绕组内部切割磁力线所感应的电动势相对于转速的比例系数,也称为发电系数或感应电动势系数。单位 V/Krpm。
1.6 转动惯量
具有质量的物体维持其固有运动状态的一种性质。电机转子和负载转动惯量之和 (单位为:kgm2),惯量会影响到速度环 PI 调节器的比例和积分增益,还有开环启动阶段的加速度。如果无法得到准确的值,可以用手转动电机和负载根据电机转子的转动惯量来大致估计整体的转动惯量。
1.7 最大电流
电机最大电流 (单位为:A) 该参数比较重要,应尽可能准确,因为涉及到电机的工作的标么电流大小。
1.8 额定转速
电机额定转速 (单位为:PRM) 电机能达到最大扭矩输出的最高转速
1.9 磁通量
磁通量 (单位为:mWb) 电机转子永磁体磁通量大小。
二、电机的一些基础公式和概念
2.1 反电动势相关
2.1.1 反电动势电压与输入电压关系
反电动势不会高于输入电压
= 供给电机的电压
= 反电动势的电压
= 电机自身的内阻所消耗的电压
2.1.1 反电动势公式
= 反电动势
= 线圈匝数
= 磁场的变化率 (T)
= (θ 为磁场方向与线圈法向的夹角)
=
(磁通量)
= 线圈截面积 (
)
= 产生磁场变化所经历的时间 (s)
2.1.2 电机定子绕组的功率关系
= 电源供给给电动机的功率(输入功率)
= 电动机输出的机械功率
= 热功损(铜损、铁损、机械损等)
2.1.3 电机定子绕组电流公式
= 反电动势
= 外加电压
= 表示电动机回路总电阻
2.2 安培力相关
安培力公式:
= 表示磁感应强度
= 表导体棒的长度
= 导体棒切割的速度
常理可知,电机反电动势不会大于供给的电压,加入我们给电机输入10V 电压,反电动势将不会超过 10V。
对于一个电机参数来说,B 和 L 是已知的,E 也不会超过输入电压,我们就可以根据这个公式推算出 v,进而得到电机空转的理论的最大值。
2.2 磁链相关
2.2.1 电机磁链常数定义 ( )
)
定义: 是永磁体在定子绕组中产生的固定磁链幅值,单位为韦伯 (Wb)。其大小由永磁体的材料特性(如剩磁 Br)、体积和充磁方向决定,理想情况下为常数,但实际受温度影响 (如钕铁硼永磁体温度每升高100℃,下降10%~15%)
电机旋转时, 切割定子绕组产生反电动势:
= 反电动势
= 电角速度
2.2.2 电机绕组磁链定义(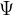 )
)
绕组磁链是指定子绕组中由电流和永磁体共同作用产生的总磁通量,单位为韦伯 (),随电流、转子位置 (
) 和时间变化,是电机控制的核心变量。
- 感磁链:由定子电流通过绕组自感 (
) 产生。
- 互感磁链:其他绕组电流通过互感耦合产生(如三相绕组间的相互作用)。
- 永磁体耦合磁链:永磁体磁场在定子绕组中的投影分量 (
)。
2.2.3 绕组磁链 (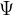 ) 和磁链常数 (
) 和磁链常数 ( ) 的区别
) 的区别
电机绕组磁链:
- 定义:与电机绕组交链的磁通总和,由电流激励或永磁体产生。
- 物理意义:反映绕组与磁场的耦合程度,直接影响反电动势和转矩。
- 动态性:随电流、转子位置变化(如Ldid为电流激励分量,ψf为永磁体固定分量)
电机磁链常数:
- 定义:永磁体单独产生的磁链,是固定值,单位韦伯(Wb)。
- 固定性:固定值 (除非温度影响Br)。
2.3 转矩方程
对于嵌入式永磁同步电机 (IPMSM) 力矩方程是:
= 永磁转矩,与q轴电流成正比
= 磁阻转矩,由 d-q 轴电感差异和电流交互作用产生。
表贴式 (SPMSM) 则是:
因为 其磁阻转矩为 0,所以控制表贴式电机获得最大转矩控制 id=0 即可。
三、定子三项电压方程:
3.1 定子三项电压方程 (磁链表达)
= 相电压
= 相电流
= 相磁链
= 相电阻
三项矩阵形式如下,其中 P 为微分算子:
其中,、
、
是三相定子电压,
是定子电阻,是是子电流,
、
、
是定子磁链,
、
、
。为电角度和实际电机角度不同,此方程组电机控制过程中应用情况较少。注意:定子磁链是一个多变量、强耦合的结果,所以用电桥测试电感时,慢速旋转电机,电感的值一直在变化。
3.2 磁链方程
电机的磁链电流产生和永磁体与绕组有关:

、
、
= 转子永磁体磁链常数
、
、
= 各自绕组的自感
、
、
= 相间互感,对称系统中
、
、
= 三项定子电流
= 永磁体磁链幅值 (常数)
= 转子 d 轴与 A 相绕组的电角度
对于 B、C 相的反电动势和角度的关系正好是相差 120°,所以上述公式需要减去和加上 。

3.3 磁链方程的微分形式
简化之前的磁链方程,此方程只描述静态系统所以忽略角度:
= 定子绕组的电感,包括自感和互感
= 永磁体磁链幅值 (常数)
如果看做成一个动态系统需要加入电角度:
我们将其取微分可得:
其中 (转子电角速度),因为最终取微分可得:
= 永磁体磁链幅值 (常数)
= 定子绕组的电感,包括自感和互感
= 电角速度
3.3 定子三项电压方程 (电感微分与磁链峰值常数表达)
还是回到这个方程:
其中磁链等于:
也就是对 取微分可得:
![]()


所以最终我们得出:

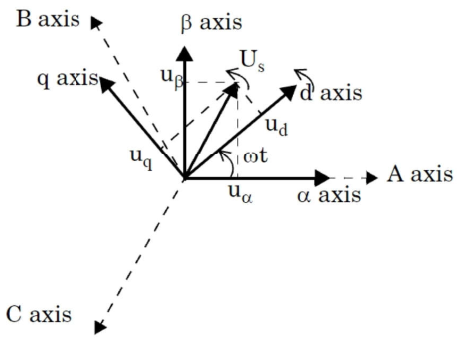
其中  矢量图如下:
矢量图如下:

四、两项电机方程
4.1 α 和 β 轴的静止电压方程
对 ABC 三相电压方程做 Clake 变换得到 uα、uβ 静止电压方程。
等价于:

eα、eβ 是两轴反电动势的公式。

这两个方程一般用作无传感器角度观测,需牢记,表贴式电机 、
相等,内嵌式电机
、
不相等。
4.2 α 和 β 轴定子磁链微分方程
该方程用于描述静止坐标系(α-β轴)下磁链随时间演化的规律。
、
= α-β 轴磁链 (反应磁场强度)
、
= α-β 轴定子电压
、
= α-β 轴定子电流
- R = 定子绕组电阻
4.3 α 和 β 轴定子磁链幅值方程
通过此公式实时计算磁链幅值,用于确定转子磁场位置(结合角度 θ=arctan(ψβ/ψα)),实现转矩和磁链的解耦控制(如矢量控制)。
= 合成磁链的幅值(单位:韦伯Wb)
、
= 静止坐标系(α-β轴)下的磁链分量,由定子电流和转子永磁体共同产生。
4.4 d 和 q 轴旋转坐标电压方程
再做 Park 变换得到两项电压 d、q 轴下的电压方程。

定子磁链方程为:

将上面的带入就可得:
= 定子电压的 d-q 分量
= 定子电流的 d-q 分量
- R = 定子的电阻
= 定子磁链的 d-q 分量
= 点角速度
= 定子 d-q 电感分量
= 永磁体磁链

4.5 d 和 q 轴的磁链方程
对于 IPMSM 电机来说 dq 轴电感不相同,公式如下:

SPMSM 电机 dq 电感轴相等,简化为:
![]()
4.6 d 和 q 轴的电磁转矩方程
= d 轴电感
= q 轴电感
= 磁链常数
= 极对数
= 电机转矩
其中,、
、
为电机本体参数,需测定。
为电机极对数。此方程已完成对耦合量解耦,最后一项和转速有关的磁链耦合量,可前馈消除,如果影响比较小,可以不用管。轴方程需牢记,电机实际控制需要用到,电流环,MTPA,弱磁等都需用到此方程。
五、坐标变换
5.1 Clark 变换和逆 Clark 变换
5.1.1 Clark 变换
左图是 A、B、C 三项电流;右图是 α、β 两项电流
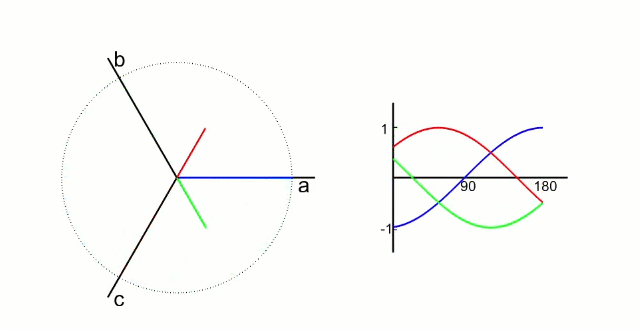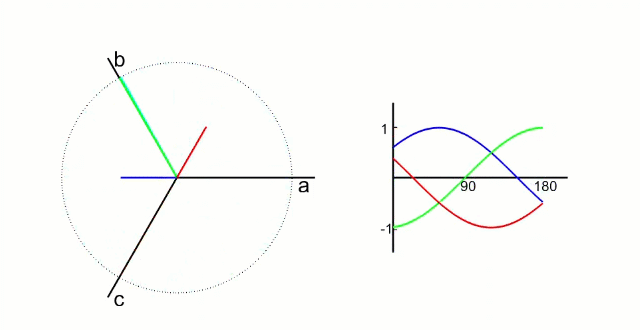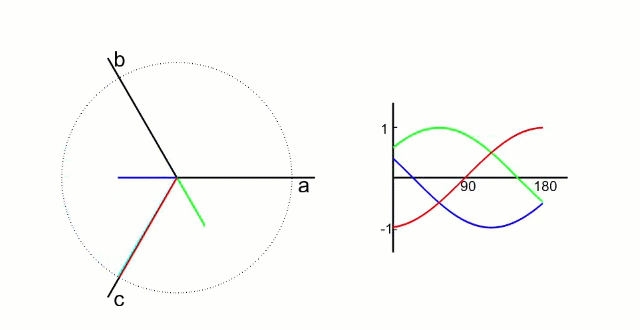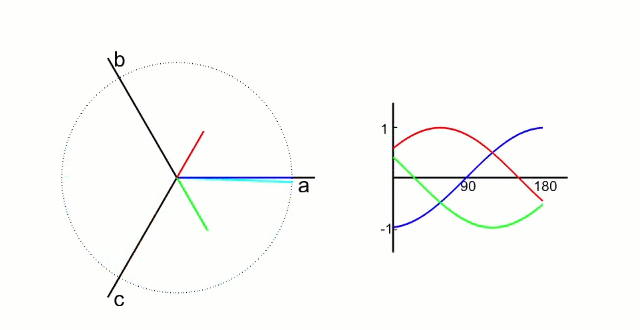
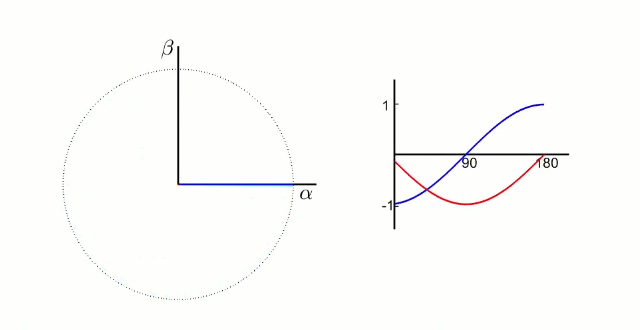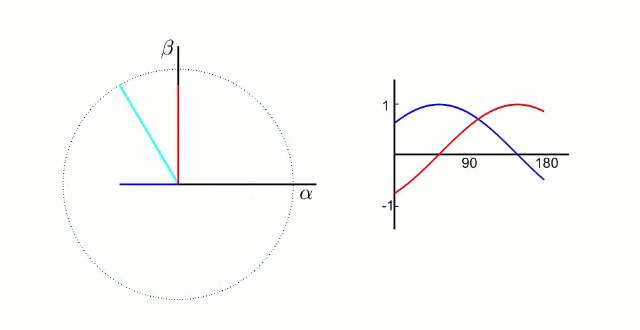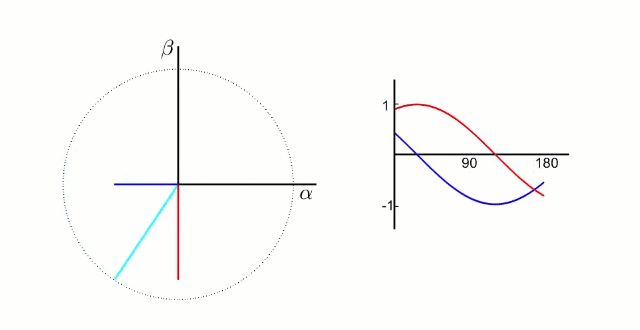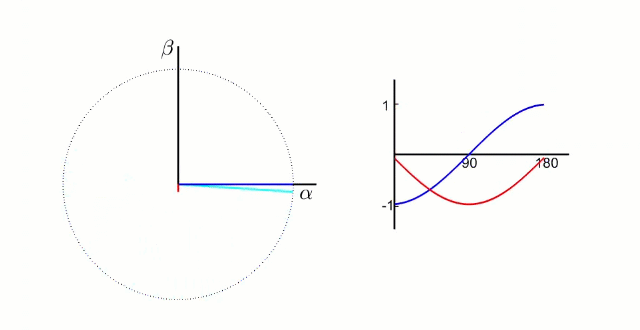
以电流变换为例,A、B、C 向 α、β 轴变换,按照幅值不变原则:
5.1.2 逆 Clark 变换
以电流变换为例,α、β 向 A、B、C 轴变换,按照幅值不变原则:
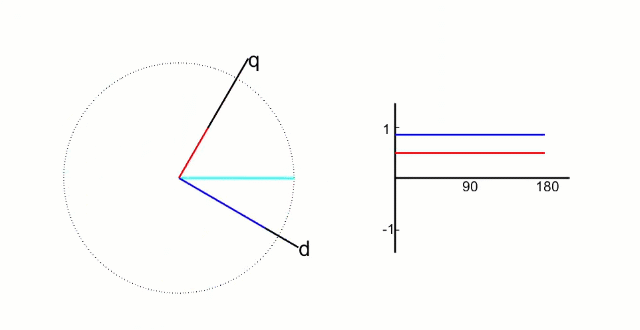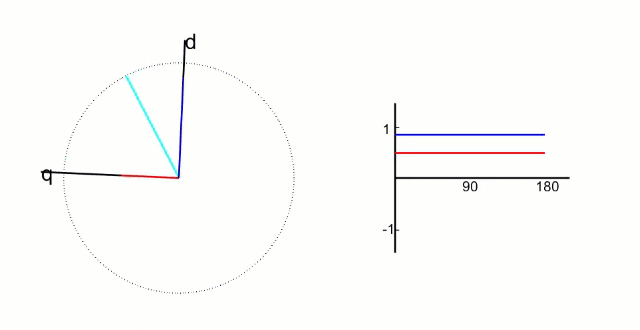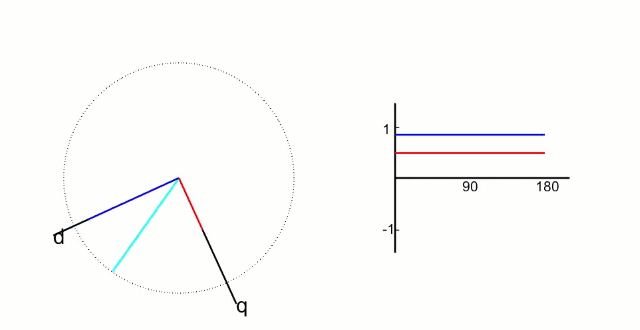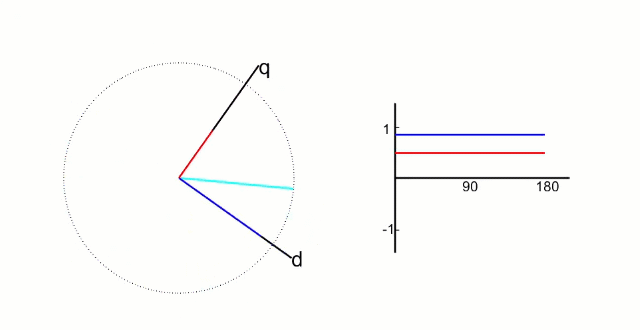
5.2 Park 变换和逆 Park 变换
左图是 α、β 两项电流;右图是 DQ 轴电流
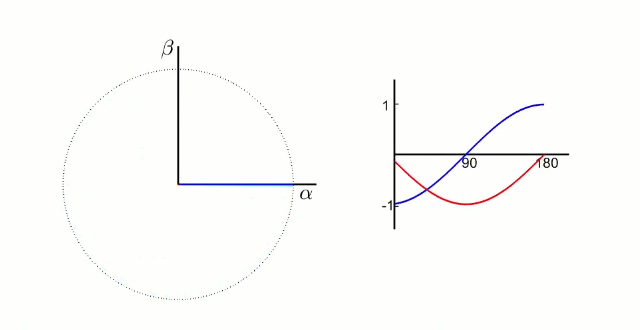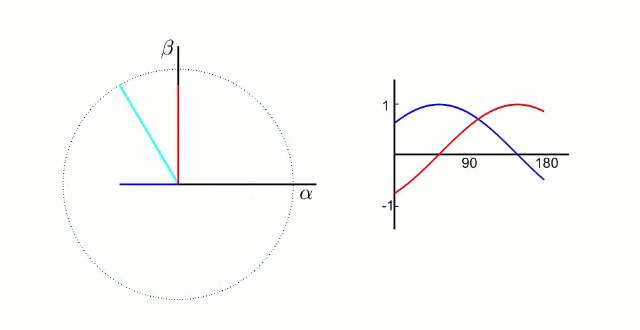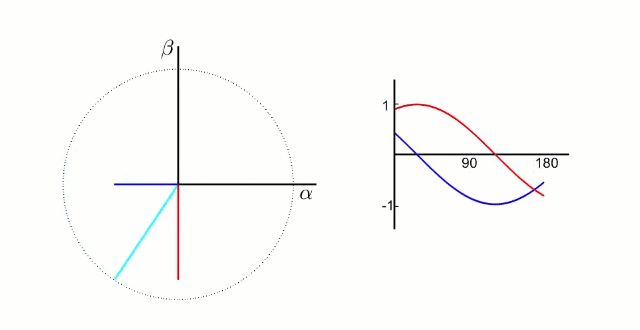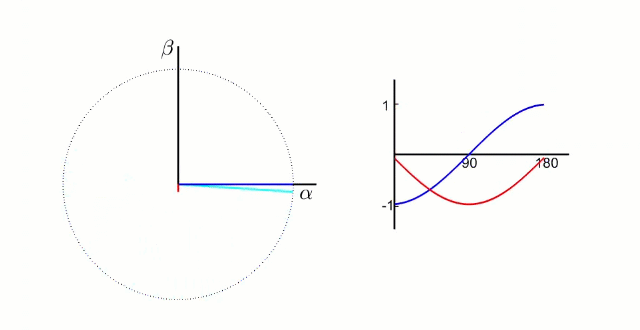

























 2702
2702

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








