关注作者了解更多
我的其他CSDN专栏
关注作者了解更多
资料来源于网络,如有侵权请联系编者
目录
(3)各分支的终点(Kg 趋于无穷)或为开环零点处或为无限点;
根轨迹法的基本概念
反馈控制系统的性质取决于闭环传递函数。只要求解出闭环系统的特征根,系统响应的变化规律就知道了。但是对于3阶以上的系统求根比较困难。如果系统中有一个可变参数时,求根就更困难了。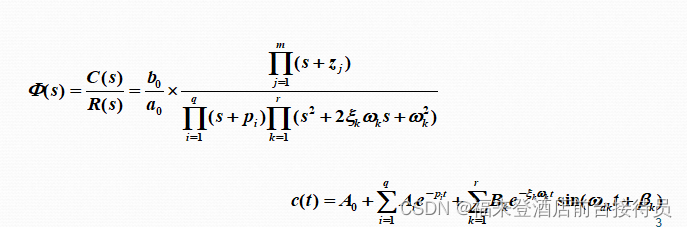
1948年,埃文斯(美国学者W.R.埃文斯)提出了一种确定系统闭环特征根的图解法——根轨迹法。在已知开环零极点分布的基础上,当某些参数变化时,利用该图解法可以非常方便的确定闭环极点。
定义:当系统开环传递函数中某一参数从0变化到正无穷时,闭环系统特征根在s 平面上的变化轨迹,就称作系统根轨迹。一般取开环传递系数(根轨迹增益Kg)作为可变参数。
举例说明:已知系统的结构图,分析0 < K < 正无穷 ,闭环特征根在s平面上的移动路径及其特征。
K为系统的开环比例系数。 Kg = 2K 称为系统的开环根轨迹增益。
求解系统闭环特征方程,求得系统闭环特征根,找出特征根的移动轨迹。
根据2阶系统根轨迹的特点,可以推得n阶系统,会有如下的结论:
(1)n阶系统有n个根,根轨迹有n条分支 ;
(2)每条分支的起点 (Kg= 0)位于开环极点处;
(3)各分支的终点(Kg 趋于无穷)或为开环零点处或为无限点;
(4)重根点,称为分离点或汇合点。
根轨迹与系统性能
1. 稳定性
当Kg从0到无穷时,图中的根轨迹不会越过虚轴进入s右半平面,因此二阶系统对所有的Kg值都是稳定的。
如果高阶系统的根轨迹有可能进入s 右半平面,此时根迹与虚轴交点处的Kg 值,称为临界开环增益。

2.稳态性能
开环系统在坐标原点有一个极点,系统属于1 型系统,因而根规迹上的Kg 值就是静态速度误差系数Kv。如果给定系统对ess 有要求,则对Kg有要求,由根迹图可以确定闭环极点位置的容许范围。
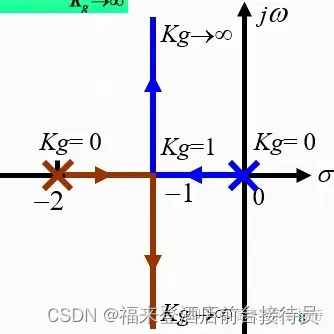
3. 动态性能
由图可见,当0 < Kg< 1时,闭环极点均位于负实轴上,系统为过阻尼系统,单位阶跃响应为非周期过程。
当 Kg = 1时,闭环两个实极点重合,系统为临界阻尼系统,单位阶跃响应为非周期过程。
当Kg > 1时,闭环极点为一对共轭复数极点,系统为欠阻尼系统,单位阶跃响应为阻尼振荡过程。
4.1.2 根轨迹方程
根轨迹的幅值方程
研究下图所示反馈控制系统的一般结构。求出系统的闭环传递函数。将系统的开环传递函数写成如下零极点表达式形式:
式中Kg为系统的根迹增益, zi 为系统的开环零点,pj为系统的开环极点。上述方程又可写为:
“-”号,对应负反馈, “+”号对应正反馈。由于满足上式的任何s都是系统的闭环极点,所以当系统的结构参数,如Kg在某一范围内连续变化时,由上式制约的s在s平面上描画的轨迹就是系统的根轨迹。因此上式称之为系统的根轨迹方程,求出根轨迹的幅值方程:
根轨迹的辐角方程

式中,k=0,±1,±2,…(全部整数)
(4-9)通常称为180 ° 根轨迹;(4-37)称作 0 ° 根轨迹。根据这两个条件,可完全确定s平面上根轨迹及根轨迹上任一点对应的Kg值。幅角条件是确定s平面上根轨迹的充要条件,因此,绘制根轨迹时,只需要使用幅角条件;而当需要确定根轨迹上各点的Kg值时,才使用幅值条件。
下面看看怎样按上式表示的幅值条件和幅角条件绘制系统的闭环根轨迹图。
已知负反馈系统开环零极点
分布如图示。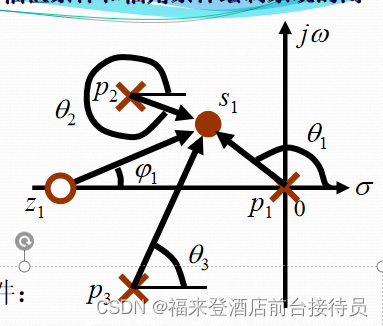
在s平面找一点s1,画出各开环零、极点到s1点的向量。检验s1是否满足幅角条件?
如果s1点满足幅角条件,则是根轨迹上的一点。寻找在s 平面内满足幅角条件的所有s1 点,将这些点连成光滑曲线,即是闭环系统根轨迹。
在1948年,埃文斯(W.R.Evdns)提出了用图解法绘制根迹的一些基本法则,可以迅速绘制闭环系统的根轨迹草图,在根轨迹草图的基础上,必要时可用幅角条件使其精确化,从而使整个根规迹的绘制过程大为简化。
4-3绘制系统根轨迹的基本法则
180º根轨迹的幅值方程:
根轨迹的幅角方程:
在下面的讨论中,假定系统变化的参数是开环根轨迹增益Kg, 这种根轨迹习惯上称之为常规根轨迹。绘制常规根轨迹的基本方法如下:
4.2.1 绘制180º根轨迹的基本法则
法则1 根轨迹的连续性
由于根轨迹增益是连续的,根也是连续的,根轨迹当然也是连续的。利用这一性质,只要精确画出几个特征点,描点连线即可画出整个根轨迹。
法则2 根轨迹的对称性
由于闭环特征根是实数或者共轭复数,因此根轨迹是关于实轴对称的。利用这一性质,只要绘制出实轴上部的根轨迹,实轴下部的根轨迹可由对称性绘出。
法则3 根轨迹的条数
n阶系统,其闭环特征方程有n个根。当Kg从0到无穷连续变化时,n个根将绘出有n条轨迹分支。因此根轨迹的条数或分支数等于其闭环特征根的个数,即系统的阶数。
法则4 根轨迹的起点和终点
根轨迹起始于系统开环极点, 终止于系统开环零点。 根轨迹上Kg= 0的点为起点,Kg趋向无穷时的点为终点。
上式说明Kg= 0时,闭环特征方程的根就是开环极点。
所以根轨迹必终止于开环零点。
在实际系统中,开环传函中 m <= n ,有m 条根轨迹终点为开环零点处,另有n-m条根轨迹的终点将在无穷远处,可以认为有n-m 个无穷远处的开环零点。
法则5 根轨迹的渐近线
根据法则4,当开环传递函数中m < n 时,将有n - m 条根轨迹分支沿着与实轴夹角为pa ,交点为qa 的一组渐近线趋于无穷远处,且有: 
法则6 实轴上的根轨迹分布
实轴上的某一区域,若 其右边开环实数零、极点 个数之和为奇数,则该区 域必是根轨迹。
“奇是偶不是”
证明:设零、极点分 布如图示:
在实轴上取一测试点s1 。
由图可见,复数共轭极点到实轴s1 点的向量幅角和为2pi,复数共轭零点亦如此。因此在确定实轴上的根轨迹时,可以不考虑复数零、极点的影响。
s1 点左边开环实数零、极点到s1 点的向量幅角均为零,也不影响实轴上根轨迹的幅角条件。
而s1 点右边开环实数零、极点到s1 点的向量幅角为pi。
如果s1 是根轨迹,则只有当零极点数目之和为奇数时,才满足幅角条件:

例4-1
设某负反馈系统的开环传递函数为
试确定系统根轨迹条数、起点和终点、渐近线及根轨迹在实轴上的分布。
解:开环极点 p1= 0、p2= -1、p3= -5。
系统的根轨迹有三条分支,分别起始于系统的三个有限的开环极点,由于不存在有限的开环零点,当Kg 趋于无穷时,沿着三条渐近线趋向无穷远处;三条渐近线在实轴上的交点
三条渐近线与正实轴上间的夹角: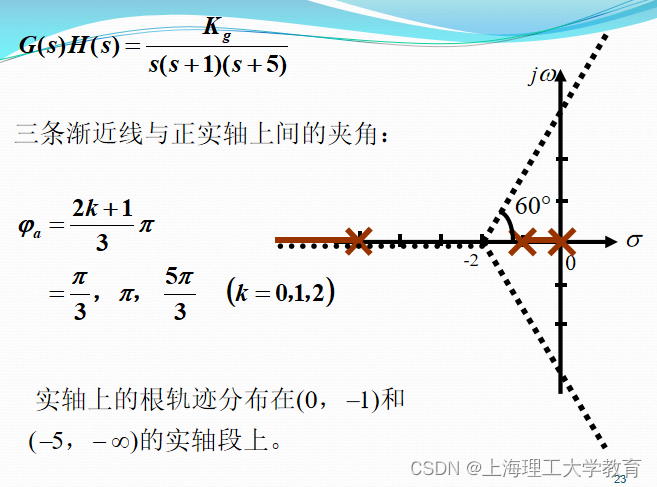
实轴上的根轨迹分布在(0,-1)和(-5,-无穷)的实轴段上。
法则7 根轨迹分离点和会合点
两条或两条以上的根轨迹在s平面上相遇后立即分开的点,称为根轨迹的分离点(会合点)。
分离点的性质:
1)分离点是系统闭环重根;
2)由于根轨迹是对称的,所以分离点或位于实轴上,或以共轭形式成对出现在复平面上; 3)实轴上相邻两个开环零(极)点之间(其中之一可为无穷零(极)点)若为根轨迹,则必有一个分离点;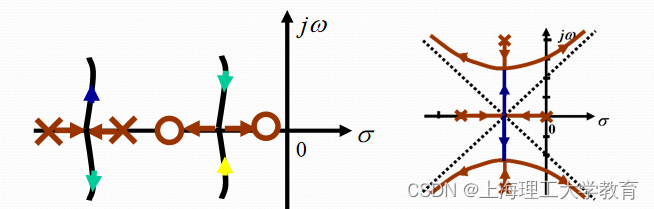
4)在一个开环零点和一个开环极点之间若有根轨迹,该段无分离点或分离点成对出现。
分离点上,根轨迹的切线与正实轴的夹角称为根轨迹的分离角,用下式计算:
确定分离点位置的方法(均需验证):
设分离点的坐标为 d,则d 满足如下公式:

式中,z i 、p j 是系统的有限开环零点和开环极点。
证明:
根轨迹在s 平面上相遇,说明闭环特征方程有重根出现,设s = d 处为分离点。
例4-2 求例4-1系统根轨迹的分离点。 
解:根据例4-1,系统实轴上的根轨迹段(-1,0),位于两个开环极点之间,该轨迹段上必然存在根轨迹的分离点。设分离点的坐标为d,则可求出分离点坐标,求出根轨迹的分离角。 
例4-3 已知系统开环传函为
试绘制系统的根轨迹。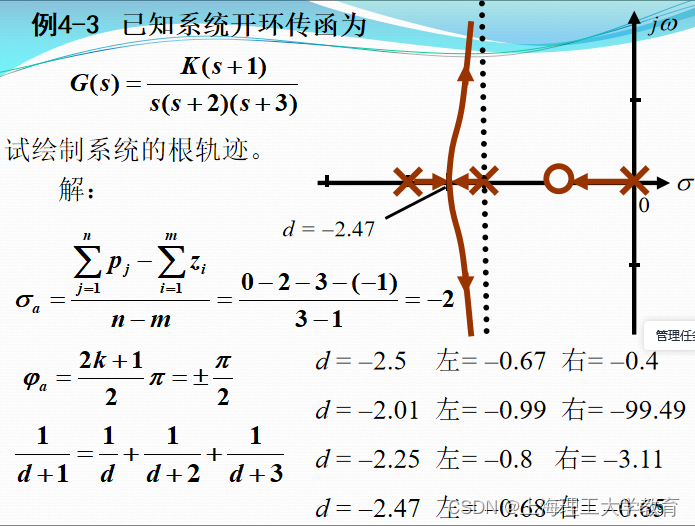
法则8 根轨迹与虚轴交点
若根轨迹与虚轴相交(临界稳定状态),则交点上的坐标(包括闭环极点和临界增益)可按下述两种方法求出:
方法一:在系统的闭环特征方程D(s) = 0中,令s = jω,D(jω) = 0的解即是交点坐标。
方法二:由劳斯稳定判据求出。
例4-5 求例4-1系统的根轨迹与s平面虚轴的交点的交点坐标。

法则9 根轨迹的出射角与入射角
根轨迹离开开环复数极点处的切线与正实轴方向的夹角,称为出射角(起始角),用 表示;
根轨迹进入开环复数零点处的切线与正实轴方向的夹角,称为入射角(终止角),用 表示

例4-4
设负反馈系统的开环传递函数为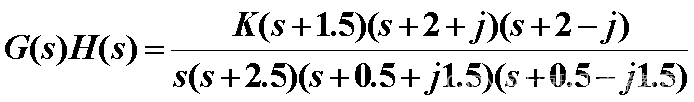
试绘制出系统的根轨迹。 解:
起始角与终止角
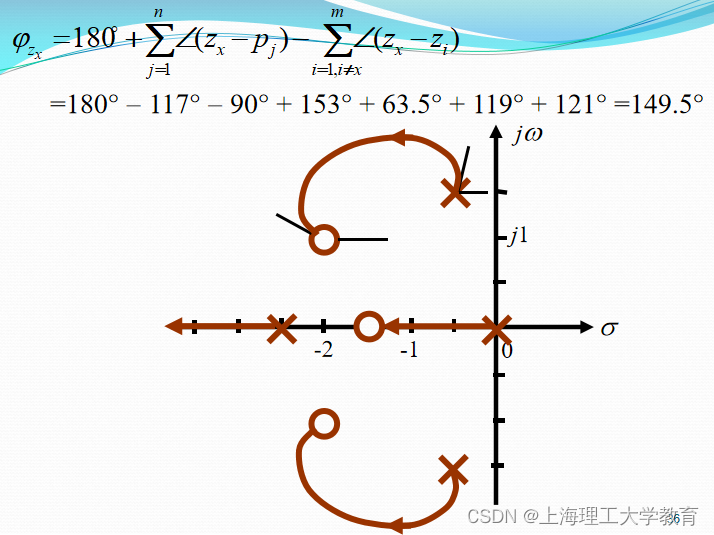
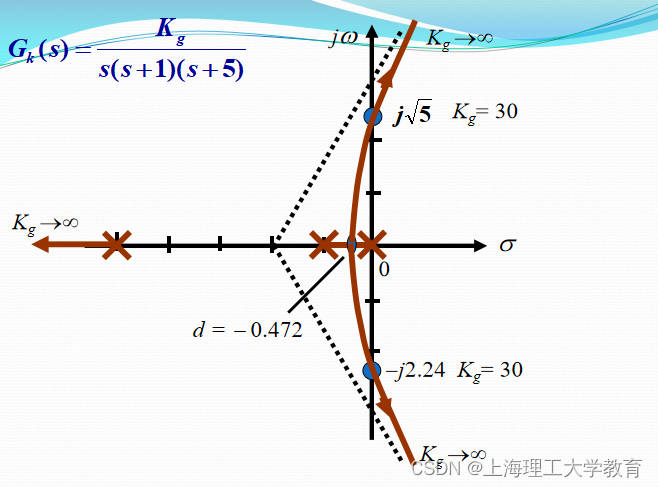
例4-6 设负反馈系统的开环传递函数为
试绘制出系统的根轨迹。
解:三个开环极点 p1= 0、p2,3 = -1 ± j 渐近线: 3条
写出渐近线和渐近线交点,根据奇偶原则写出实轴上的根轨迹,画出大致轮廓,可知根轨迹过虚轴,再求出根轨迹与虚轴的交点。
汇出根轨迹如图所示:

法则10 闭环极点的和与积
绘制根轨迹,或利用根轨迹进行系统性能分析时,可利用该法则。 若开环传函分母阶次n比分子阶次m高2次或2次以上,即n - m >= 2,则系统闭环极点之和等于其开环极点之和。

利用上述基本法则,可以迅速绘制闭环系统的根轨迹草图,对需要准确绘制的根轨迹,可根据幅角方程条件使其精确化,一般而言,靠近虚轴或原点附近的根轨迹对分析系统的性能至关重要,应尽可能的准确绘制。
资料仅供学习使用
如有错误欢迎留言交流
上理考研周导师的其他专栏:
上理考研周导师了解更多

























 637
637

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










