关注作者了解更多
我的其他CSDN专栏
关注作者了解更多
资料来源于网络，如有侵权请联系编者
目录
w由0变到无穷 时的开环幅相频率特性G(jw)对(-1,j0)点的总包围次数为
系统稳定的充分必要条件是系统闭环特征根都具有负实部，即位于s左半平面。在时域分析中判断系统的稳定性，一种方法是求出特征方程的全部根，另一种方法就是使用劳思-赫尔维茨稳定判据（代数判据）。然而，这两种方法都有不足之处，对于高阶系统，非常困难且费时,也不便于研究系统参数、结构对稳定性的影响。
特别是，如果知道了开环特性，要研究闭环系统的稳定性，还需要求出闭环特征方程，无法直接利用开环特性判断闭环系统的稳定性。而对于一个自动控制系统，其开环数学模型易于获取，同时它包含了闭环系统所有环节的动态结构和参数。
除劳斯判据外，分析系统稳定性的另一种常用判据为奈奎斯特（Nyquist）判据。Nyquist稳定判据是奈奎斯特于1932年提出的，是频率法的重要内容，简称奈氏判据。奈氏判据的主要特点有
1.根据系统的开环频率特性，来研究闭环系统稳定性，而不必求闭环特征根；
2.能够确定系统的稳定程度（相对稳定性）。
3.可用于分析系统的瞬态性能，利于对系统的分析与设计；
4.基于系统的开环奈氏图，是一种图解法。
5.3.1 简化奈奎斯特稳定判据
1
绘制 开环幅相频率特性 G(jw) 逆时针包围 (-1,j0)点的圈数为 N ，若 已知系统开环右半平面极点数为 P ，则系统闭环右半平面极点个数为 Z （不包括虚轴上的极点）：
则 Z = P -2 N
当Nyquist曲线G(jω) 通过(-l, j0)点时, 表明系统在s平面虚轴上有闭环极点，系统处于临界稳定状态，属于不稳定。
2.采用穿越的概念简化复杂曲线包围次数的计算
开环频率特性曲线要形成对(-1,j0)点的一次包围，势必穿越（-∞，-1）区间一次。
开环频率特性曲线逆时针穿越（-∞，-1）区间时，随ω增加，频率特性的相角值增大，称为一次正穿越N’+。（逆时针正） 反之，开环频率特性曲线顺时针穿越（-∞，-1）区间时，随ω增加，频率特性的相角值减小，则称为一次负穿越N’-。（顺时针负）
频率特性曲线包围(-1,j0)点的情况，就可以利用频率特性曲线在负实轴（-∞，-1）区间的正、负穿越来表达。
w由0变到无穷 时的开环幅相频率特性G(jw)对(-1,j0)点的总包围次数为
N = （ N’+ - N’- ）
利用正、负穿越情况的奈奎斯特稳定判据叙述为：
Z = P -2（ N’+ - N’- ）
注意奈氏曲线在 (-1,j0)点以右负实轴上相位有变化不算穿越。
3.半次穿越
奈氏曲线始于或止于(-1,j0)点以左负实轴，称为一个半次穿越，如图所示。
[例5.9]
某系统开环传递函数如下，试判断闭环系统的稳定性。
由于曲线始于（-3，j0）点，故顺时针包围（-1，j0）点的次数为1/2，N’-=1/2。由于开环右极点数为P=0，故
Z = P-2（ 0-N’- ） = P+2N’- =1
闭环系统有一个右极点，闭环不稳定。
[例5.10]
经实验测得某最小相位系统的开环奈氏图如图所示，判断闭环稳定性。
由于为最小相位系统，开环右极点数P=0，且为0型系统，故直接利用开环频率特性G(jw)的轨迹判断稳定性。
由图可以看出,当由0变到+无穷时, G(jw)矢量在(-1,j0)点以左负实轴上正负穿越次数各一次。 Z = P -2（ N’+ - N’- ） =0。
故由奈氏稳定判据知该闭环系统是稳定的
4.型别v≥1系统开环频率特性G(jw)曲线的处理
（1）先画出曲线的起点对应于w=0+，然后逐渐增加到无穷远的曲线。
（2）在w=0附近, 幅相特性以无穷为半径,在原曲线上 逆时针补画角度= v·90° 的圆弧，添加圆弧后相当于得到新的开环频率特性G(jw)曲线。
（3）所指曲线仍为w由0变到+无穷时的开环幅相频率特性G(jw) 。
当系统的开环奈氏曲线作如上处理后，代入简化奈氏稳定判据即可，且系统在虚轴上的0值开环极点作左极点处理。 、
Z = P -2（ N’+ - N’- ）
[例5.11]
判断图示系统的闭环稳定性
Z = P -2（ N’+ - N’- ）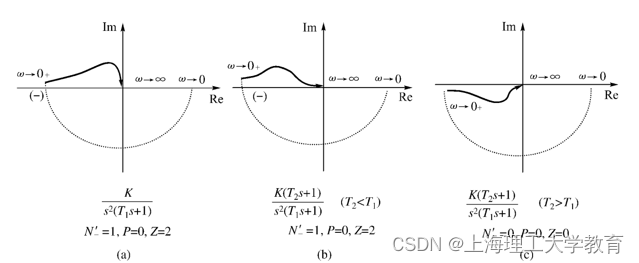
由以上分析可知，开环系统型别过高会影响稳定性，而串联比例微分调节器可以改善系统的稳定性，起到校正的作用，但要选择合适的参数。
[例5.12]
判断图示系统的闭环稳定性
Z = P -2（ N’+ - N’- ）
b图所示系统为一Ⅰ型二阶系统，该系统为非最小相位系统，P=1，在w=0附近,曲线以正无穷为半径,逆时针补画角度= 1·90°=90°的圆弧与负实轴相交。w由0变到+无穷 时，顺时针包围（-1，j0）点半次，有N’-=1/2。则Z = 2N’-+ P=2，闭环系统有两个右极点，系统不稳定。
5.4 控制系统的相对稳定性
当系统处于稳定状态，且接近临界稳定状态时，虽然从理论上讲，系统是稳定的,但实际上，系统可能已处于不稳定状态。其原因可能是在建立系统数学模型时，采用了线性化等近似处理方法；或系统参数测量不准确；或系统参数在工作中发生变化等。
因此要求系统保有一定的相对稳定性（稳定裕度），这样才可以保证不致于分析设计过程中的简化处理，或系统的参数变化等因素而导致系统在实际运行中出现不稳定的现象。
系统稳定裕度用于表征系统的相对稳定程度，经常作为控制系统的频率域性能指标。
可知：K值较小时，系统稳定；K值较大时，系统不稳定的；K取两者间的某个值时，Nyquist曲线通过(-1,j0)点，系统处于临界稳定状态。系统Nyquist曲线与实轴交点坐标离(-1, j0)点的距离，可作为表征系统相对稳定性的一个指标。
通常用相角裕量r和幅值裕量hg表示系统稳定裕度。
一.稳定裕度的定义
稳定裕度包括相角裕度和幅值裕度两个概念
系统的开环幅相曲线如图：a点为相角裕度，b点为幅值裕度
二.稳定裕度和系统稳定性的关系
最小相位系统临界稳定时G(jw)曲线过(-1,j0)点，该点：
相角裕度的含义：保持系统稳定的前提下，开环频率特性的相角允许增加的滞后角度。
幅值裕度的含义：保持系统稳定的前提下，开环频率特性的幅值允许增加到的倍数。
对于Z=0，P=0的最小相位系统，如果要稳定，须使奈氏曲线在GH平面内围绕（-1，j0）的圈数为0。
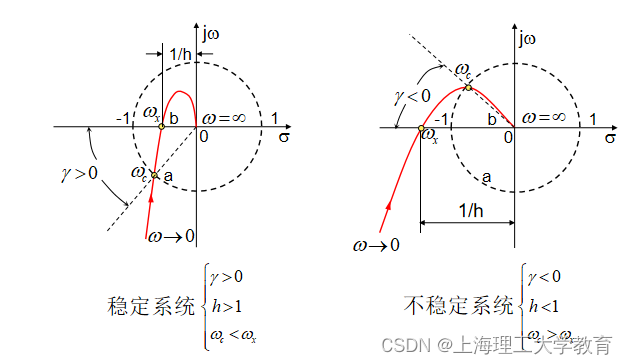
仅用相角裕量或幅值裕量都不能较全面地描述系统的相对稳定性。上图两个系统的暂态响应都是很差的，系统的相对稳定性也很差。通常相角裕量g取300～600，幅值裕量h>2【即A(wx)<0.5】。
5.5 对数频率特性及其绘制
5.5.1 对数频率特性曲线基本概念 （重点）
对数频率特性图（Bode图）将幅频和相频特性分别画出，并按对数分度运算，使系统的分析和设计变得十分简便。
1. 伯德（ Bode ）图的构成
对数幅频特性图的横坐标是对w取以10为底的对数进行分度的。
标注角频率的真值,以方便读数。w每变化十倍,横坐标1gω就增加一个单位长度，记为decade或简写dec,称之为“十倍频”或“十倍频程”。
横坐标对于ω是不均匀的，但对1gω却是均匀的线性分度。由于0频无法表示，横坐标的最低频率是由所需的频率范围来确定的。
若横轴上有两点ω1与ω2，则该两点的距离不是ω2-ω1，而是lgω2-lgω1，如2与20、10与100之间的距离均为一个单位长度，即一个十倍频程。
确定Bode图坐标系
纵坐标是对幅值分贝(dB)数进行分度，用L(w)=20 lgA(ω)表示。
对数相频特性图的横坐标分度方法同对数幅频特性，而纵坐标则对相角进行线性分度，单位为度o, 仍用p (w)表示。
对数频率特性曲线坐标系如图所示，在绘制函数关系时，相当于lgω为自变量。
在极坐标中绘制幅相频率特性,要花较多时间，而在绘制对数幅频特性时,可以直接相加。
2．Bode图法的特点
（1）横坐标按频率w取对数分度，低频部分展宽，而高频部分缩小。与对实际控制系统（一般为低频系统）的频率分辨要求吻合。
（2）幅频特性取分贝数［20Lg|GH|］后，使各因子间的乘除运算变为加减运算，在Bode图上则变为各因子幅频特性曲线的叠加，大大简化了作图过程，使系统设计和分析变得容易。
（3）可采用由直线段构成的渐近特性（或稍加修正）代替精确Bode图，使绘图十分简便。 （4）在控制系统的设计和调试中, 开环放大系数K是最常变化的参数。而K的变化不影响对数幅频特性的形状，只会使幅频特性曲线作上下平移。
5.5.2 典型环节的伯德图
1.比例环节
说明比例环节可以完全、真实地复现任何频率的输入信号，幅值上有放大或衰减作用； p(w)=0º,表示输出与输入同相位，既不超前也不滞后。
2. 积分环节( G(s)= 1/s )
频率每增加10倍，幅频特性下降20dB，故积分环节的对数幅频特性是一条斜率为-20dB/dec的斜线,并且在w=1这一点穿过0dB线。
表明积分环节是低通滤波器，放大低频信号、抑制高频信号，输入频率越低，对信号的放大作用越强；并且有相位滞后作用，输出滞后输入的相位恒为90º。
3. 微分环节（ G(s)= s）
微分环节的对数幅频特性是一条斜+20dB/dec的斜线,并且在w=1这一点穿过0dB线。
积分环节与理想微分环节的对数幅频特性相比较，只相差正负号，二者以轴为基准，互为镜象；同理，二者的相频特性互以w轴为镜象。
可见，理想微分环节是高通滤波器，输入频率越高,对信号的放大作用越强；并且有相位超前作用，输出超前输入的相位恒为90º，说明输出对输入有提前性、预见性作用。
4.惯性环节
为简化对数频率特性曲线的绘制，常常使用渐近对数幅频特性曲线（特别是在初步设计阶段）。
1.低频段
在Tw<<1(或w<<1/T)的区段,可以近似地认为Tw=0,从而有故在频率很低时,对数幅频特性可以近似用零分贝线表示,这称为低频渐近线。
2.高频段
在Tw>>1(或w>>1/T)的区段,可以近似地认为 L(w)为因变量，lgw为自变量，因此对数频率特性曲线是一条斜线, 斜率为-20dB/dec, 称为高频渐近线，与低频渐近线的交点为wT =1/T，wT 称为转折频率，是绘制惯性环节的对数频率特性时的一个重要参数。
精确值与渐近线的误差
同时，如需由渐近对数幅频特性曲线获取精确曲线，只须分别在低于或高于转折频率的一个十倍频程范围内对渐近对数幅频特性曲线进行修正就足够了。
（2）对数相频特性
精确相频特性为: p(w) = -arctan (ωT)；
对数相频特性曲线将对应于ω=1/T及p(w)=-45°这一点斜对称，如图所示，可以清楚地看出在整个频率范围内，p(w)程滞后持续增加的趋势，极限为-90。
当惯性环节的时间常数T 改变时，其转折频率1/T 将在Bode图的横轴上向左或向右移动。与此同时，对数幅频特性及对数相频特性曲线也将随之向左或向右移动，但它们的形状保持不变。
惯性环节的幅相曲线如图所示
5．一阶微分环节（G(s)=Ts＋1）
1. 低频段 在Tw<<1(或w<<1/T)的区段,对数幅频特性可以近似用零分贝线表示,为低频渐近线。 2.高频段 在Tw>>1(或w>>1/T)的区段,可以近似地认为 高频渐近线是一条斜线, 斜率为20dB/dec, 当频率变化10倍频时,L(w)变化20dB。转折频率为wT=1/T。
可知,一阶微分环节的对数幅频特性和相频特性与惯性环节的相应特性互以横轴为镜像。精确曲线的修正方法也与惯性环节相同。但需要注意到修正值的符号相反。如转折频率处wT对应的精确值是L（wT）=0+3=3dB。
一阶微分环节具有放大高频信号的作用，输入频率w越大，放大倍数越大；且输出超前于输入，相位超前范围为0º→90º，输出对输入有提前性、预见性作用。
一阶微分环节的典型实例是控制工程中常用的比例微分控制器（PD控制器），PD控制器常用于改善二阶系统的动态性能，但存在放大高频干扰信号的问题。
6．二阶振荡环节
（1）对数幅频特性
1.低频段 Tw<<1(或w<<1/T)时，L(w) = 20lg1=0dB，低频渐近线与0dB线重合。
2.高频段 Tw>>1(或w>>1/T)时,并考虑到（0≤阻尼≤1），有 L(w)= -20lg(Tw)2= -40lg(Tw)=-40lgT-40lgw dB 这说明高频段是一条斜率为-40dB/dec的斜线,称为高频渐近线。
wT=1/T为低频渐近线与高频渐近线交点处的横坐标，称为转折频率，也就是环节的无阻尼自然振荡频率wn。
图像
（2）相频特性
8．延迟（滞后）环节（G(s)=e-Ts）
p(w)是呈指数规律下降的曲线，随ω增加而滞后无限增加，
关注作者了解更多
我的其他CSDN专栏
关注作者了解更多
资料来源于网络，如有侵权请联系编者
扫一扫
3467
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
