引入:
看到这个理论我们第一反应是傅里叶变换是什么以及为什么提出?
相比于傅里叶变换我们最先接触到的是傅里叶级数,那我们先来看一下傅里叶级数的定义:
傅里叶级数:
任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示。
第一步开始思考问问题:周期函数是什么形式的?为什么要是周期函数?周期函数有哪些特点?任何周期函数的前提条件是什么?函数形式有哪些?为什么要用级数来定义呢?一定是无穷级数吗?为什么是无穷级数?以及最重要的为什么要提出傅里叶级数?
第二步我们开始试着定性理解它的概念并对以上问题做出解释:
1)为什么要提出傅里叶级数
在实际生活中周期函数往往用来描述周期现象,最常见的周期函数我们可以定义为:
该表达式也就是在周期函数在时域上的时间关于振幅的函数表达式。
正余弦函数具有非常多优良的性质:连续性、周期性、奇偶性等等。而在实际生活中的周期函数往往并不是这样简单,更多的是方波、毫米波雷达中的FMCW调频连续波等等。于是傅里叶就设想,能不能以一种简单的波为基础进行叠加,得到其他的波形。换言之,可以将复杂的波形拆解为简单的正弦余弦波,再进行进一步的研究计算。傅里叶这个想法非常伟大,他从一种简单情形推广到复杂的情形的理论,并且还是真的成立的!于是傅里叶在求解热传导方程中定义傅里叶级数(即一系列正弦波)为:
对表达式中的三角函数进行展开以及常数项合并,得到三角函数表达式:
利用三角函数在一个周期内的积分为0的正交性,可以得到:
将参数回代入三角函数表达式,就得到了周期函数在频域上频率关于时间的表达式。
信号角度理解一下,三角表达式中我们可以将 理解为无法通过正余弦信号叠加得到的直流通量,也就是我们在信号分解中见到的“直线”,如图所示:

复杂信号分解图(傅里叶思想)
总结一下:
任何一个满足勒贝格条件傅里叶级数的结论是多方面的:
1.它的周期函数都可以分解成一个直流分量和一系列正弦余弦函数之和(也就是他们的级数)。
2.该函数中的参数( )可以用周期函数的积分表达式来表示出.
2)周期函数的形式
首先我们观察三角函数形式的表达式,可以与“宇宙最帅公式—欧拉公式”联系起来:
于是在此理论基础上,代入傅里叶级数三角表达式,可以将周期函数转化为指数表达式:
其中,
,周期
确定了
就确定了;
,
以下为 推导过程:
将指数形式的傅里叶展开式中的 的单独一项列出来:
等式两端同时乘以 :
等式两端同时积分得:
根据复指数信号的正交性得:
三角函数形式更多的是在实数域上的表现形式,我们知道实数域是复数域的一个子集,指数形式的表达式将傅里叶级数表达式推广到复数域上,使得傅里叶级数更加一般化,在实际应用中也更为常用。由于在三角函数形式的傅里叶级数中,n大于等于1,因此频谱的横坐标只有正数,这种频谱也被称为单边频谱;复数形式的n即存在正值也存在负值,其频谱图中幅值是偶对称的,相位是奇对称,为双边频谱。
故傅里叶断言:任何周期信号都可以表示为谐波关系的虚指数信号的线性组合。
3) 周期函数的限制条件
在实际情况中几乎所有的周期函数都可以满足傅里叶级数展开的条件;而在理论研究中,需要限制其满足狄利克雷条件:
(1)在一个周期内,连续或只有有限个第一类间断点;
(2)在一个周期内,极大值或者极小值的数目应该是有限个;
(3)在一个周期内,信号是绝对可积的。
4)解答一下剩下的最初提出的问题
周期函数是什么形式的?——常数形式或者
为什么要是周期函数?——只有周期函数的频域图是离散的,也就是可以被分解的;非周期函数的频域图是连续的,无法直接通过傅里叶级数展开。(时域的周期性对应于频域的离散性)。

连续周期函数的时域图(左)、频域图(右)

非周期信号的时域图
非周期信号的频域图
注:实际生活中由于一般信号的长度是有限的,故“非周期“信号更为常见。
常见的非周期信号有:单边指数信号、举行脉冲信号、符号函数、单位脉冲信号、直流信号、单位阶跃信号。具体频域时域图见信号与系统(4)——常见非周期信号频谱_单边指数信号的频谱-CSDN博客
周期函数有哪些特点?——频谱特性:离散性;谐波性(线条只出现在基波频率整数倍的波点上);收敛性(信号的幅频随着频率趋向无穷大而趋于0)。
任何周期函数的前提条件是什么?——狄利克雷条件
函数形式有哪些?——三角函数形式:
复数形式:
为什么要用级数来定义呢?——谐波函数的“叠加“就可以理解为是正弦函数求和,即其级数
以及最重要的为什么要提出傅里叶级数?——分解复杂波形,通过简单波形分析复杂问题
接着我们可以来研究傅里叶变换了:
傅里叶变换(FT:Fourier Transform)
表示能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。
依旧是提出问题:看到这个定义不要看完就划走,那我们开始思考:什么是变换?为什么要变换?谁可以进行变换?变换成什么样?不同条件下变换结果会有不同吗?变换之后原来与现在的异同?
1)物理意义上定性理解定义
首先来聊聊变换的话题:傅里叶变换中“变换”体现在将时域信号转换到频域信号中,那为什么要变换呢?在傅里叶级数的背景下我们可以知道,想要将复杂信号分解为简单的正余弦函数,为了更加明显我们通常用图(a)来理解其叠加的方式。(b)图即(A-t图)便是我们通常说的时域图,它具体表现为振幅关于时间的函数,也就是我们接触最多的函数图像,它反映了在时间维度上某一时刻信号的状态。图(c)即(A-f)图便是频域图,也称为频谱图,是振幅关于频率的函数,它可以反应不同频率成分的振幅。在(c)图中我们可以直观的看到频率的分支以及其对应振幅的大小。经过一次傅里叶变换就可以将时域图转化为频域图,即说明傅里叶变换之后可以提取出不同频率的信号分量!

一维傅里叶变换时域(b)频域(c)图
2)思考一下谁可以变换
对于傅里叶级数是限制了周期函数的前提,但傅里叶变换并没有限制这个条件(因为实际生活中非周期的情况会更多,所以傅里叶变换也是一种对傅里叶级数的推广),也就是说非周期函数在一定条件下也可以分解?那需要满足什么条件呢?
设想一下:非周期的信号是不是可以看作周期无穷大的周期信号?在这个思路下我们将傅里叶级数进行推广:
预备公式:
傅里叶级数复数形式:
当 时,原来的级数可以化作积分形式:
即可推导出频域上的函数:
结合时域频域图像理解一下:

傅里叶变换原理时域图(左)、频域图(右)
非周期连续信号其实本质上我们还是可以通过傅里叶级数进行变换,为什么呢?这就要追溯到我们所学习的“延拓”——将函数的定义域人为扩大,我们通过奇延拓与偶延拓,可以将原本非周期的信号转化为周期信号,再对它进行傅里叶变换。来张图理解一下:
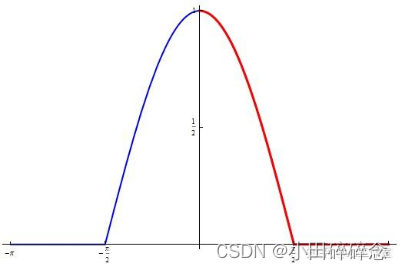
偶延拓

奇延拓
下节预告:离散时间傅里叶变换以及离散傅里叶变换的产生及应用


























 4719
4719

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








