matlab simulink三自由度汽车模型

 

 

 

 

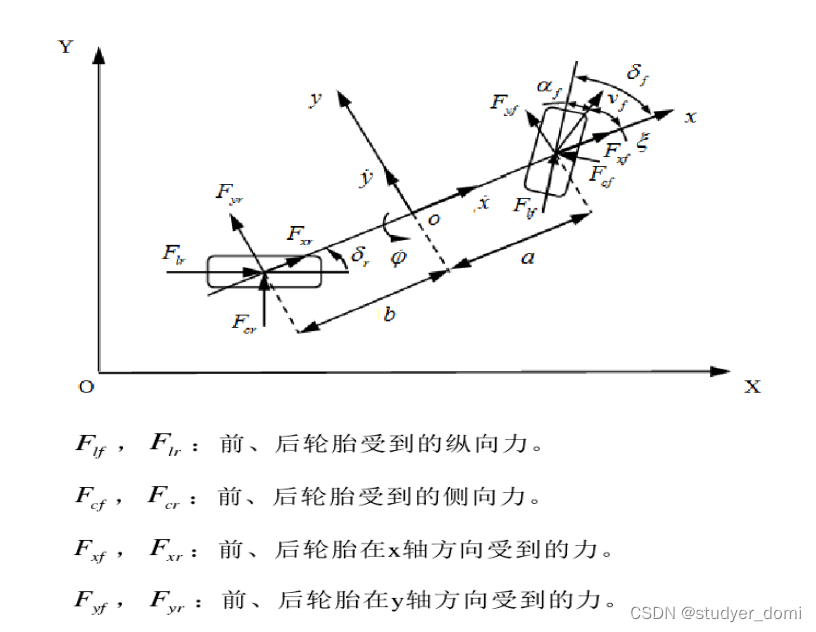
由牛顿第二定理在x,y,z轴上有：

轮胎的纵向力和侧向力可以表示如下：

前轮车速与x轴夹角可表示为：

前后轮胎侧偏角：

前后轮胎侧偏力：

前后轮胎纵向力：

车辆坐标系与车身坐标系之间的转换：

从而有：

 clear
clc
close all
V=80/3.6;%车速
Sf=0.2; Sr=0.2;
sf=0.2; sr=0.2;
%syms a b;%前后车轮距离车辆质心的距离，车辆固有参数
a=1.232;b=1.468;
%syms C_cf C_cr C_lf C_lr;%分别为前后车轮的纵横向侧偏刚度，车辆固有参数
Ccf=66900;Ccr=62700;Clf=66900;Clr=62700;
%syms m g I;%m为车辆质量，g为重力加速度，I为车辆绕Z轴的转动惯量，车辆固有参数
m=1723;g=9.8;I=4175;
% 车辆动力学模型求解