电容二极管升压电路分析

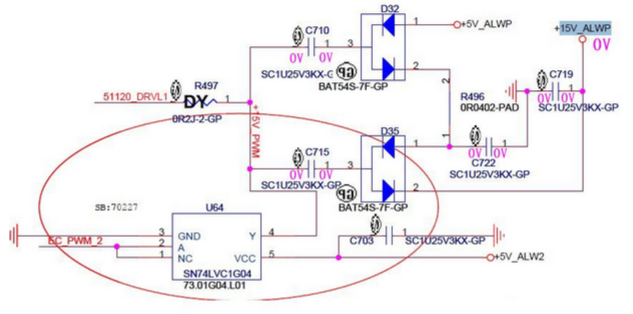
当电路未通电时，各处电平都是0V。

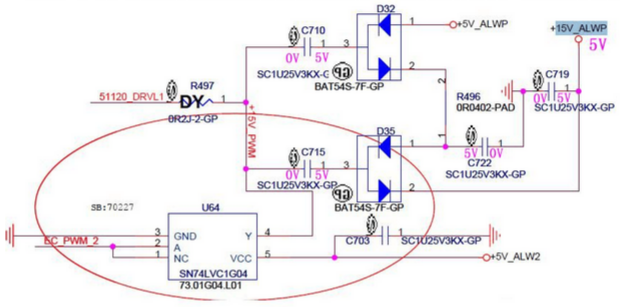
当通电时，右上角+5V_ALWP通过D32的1引脚对C710、C722、C715、C719进行充电，此时电容上两端的电位如上图所示。此时+15V_ALWP输出端口的实际电平为5V。

当U64的Y引脚开始输出幅值为5V的方波，当Y第一次处于5V电位时：

1.由于电容两端的电压不能突变，此时C715两端的电压为左边5V，右边为10V，然后电流经过D35的2引脚对C719电容充电，充完电后C719的电压升到了10V。

2.同时，Y输出的5V也对C710进行充电，C710两端的电压为左边5V，右边为10V，然后电流经过D32的2引脚对C722进行充电，充完电后C722的电压升到了10V。

此时+15V_ALWP输出端口的实际电平为10V。

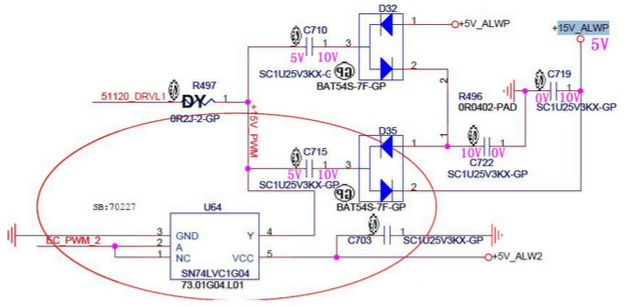
当U64的Y引脚开始输出幅值为5V的方波，当Y第一次处于0V电位时：

1.由于电容两端的电位不能突变，此时C715两端的电压为左边0V，右边5V。当C715电压为5V后，由于C722电压10V大于C715的5V，C722会对C715充电。充电后C715=C722=7.5V。此时C715的电压依然比C719的电压低。但是由于D32二极管反向截止，所以C719不会对C715充电。C719的电压保持在10V。

2.同时，C710的电压为左边0V，右边5V，C722的左端电压为7.5V，由于D32的2引脚的反向截止，C722依然不会对C710充电，C722保持在7.5V。

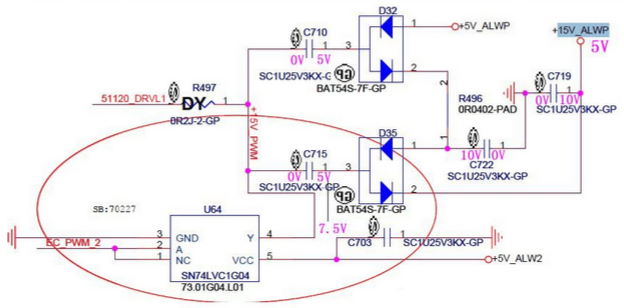
当Y第二次处于5V时，C722通过C710、D32的2引脚又被充电为10V。当Y又处于低电平时，C722（10V）对C715（7.5V）充电。C715的电压变为8.75V。经过数次过程后，C715两端的电压差上升为了10V，当Y再次为5V时，C715的右端的电位变为了15V。当然，在整个过程中，C715都在通过D35的2引脚向C719充电。

最终+15V_ALWP输出端口的电平变为了15V。