文章目录
矩阵是一个数学工具,它可简化的问题:线性方程,线性变换,投影、最小二乘法、回归、SVD、PCA、图像处理、优化、机器学习、密码学,让复杂的公式变得简洁起来是矩阵的重要作用之一
一 基本概念
1.1 定义

数学上,一个m*n的矩阵是一个由m行(row)n列(column)元素排列成的矩形阵列。矩阵里的元素可以是数字、符号或数学式。
1.2 常见矩阵
| 名称 | 特征 |
|---|---|
| 零矩阵 | 所有元素均为0 |
| 对角矩阵 | 对角线元素不全为0,其他元素为0 |
| 非奇异矩阵 | 行列式不为 0 的矩阵;也称为可逆矩阵 |
| 实对称矩阵 | AT == A,即aij= aji |
| 正交矩阵 | ATA = E |
| 正定矩阵 | 非0向量x使得XTAX>0 |
| 反对称阵 | AT == -A,即aij=- aji,aii=0 |
| 同型矩阵 | 矩阵A,B的行、列数相同 |
| 行最简矩阵 | 非零行主元(该行最左边的第1个非零元)为1且主元所在列其他元素为0 |
| 矩阵相等 | 对应位置元素都相同 |
| 矩阵等价 | 定义:B=QAP,A经过初等变换后变为B;充要:同型且秩等 |
1.3 伴随矩阵
定义
A = ( a 11 a 12 ⋯ a 1 , n − 1 a 1 , n a 21 a 22 ⋯ a 2 , n − 1 a 2 n ⋮ ⋮ ⋮ ⋮ a n − 1 , 1 a n − 1 , 2 ⋯ a n − 1 , n − 1 a n − 1 , n a n 1 a n 2 ⋯ a n , n − 1 a n n ) A=\left(\begin{array}{ccccc}a_{11} & a_{12} & \cdots & a_{1,n-1} & a_{1,n} \\ a_{21} & a_{22} & \cdots & a_{2,n-1} & a_{2n} \\ \vdots & \vdots & & \vdots & \vdots \\ a_{n-1,1} & a_{n-1,2} & \cdots & a_{n-1, n-1} & a_{n-1, n} \\ a_{n1} & a_{n2} & \cdots & a_{n, n-1} & a_{n n}\end{array}\right) A= a11a21⋮an−1,1an1a12a22⋮an−1,2an2⋯⋯⋯⋯a1,n−1a2,n−1⋮an−1,n−1an,n−1a1,na2n⋮an−1,nann
为n阶矩阵,|A|中aij的余子式为Mij,代数余子式为Aij,称
A ∗ = ( A 11 A 21 ⋯ A n − 1 , 1 A n 1 A 12 A 22 ⋯ A n − 1 , 2 A n 2 ⋮ ⋮ ⋮ ⋮ A 1 , n − 1 A 2 , n − 1 ⋯ A n − 1 , n − 1 A n − 1 , n A 1 n A 2 , n ⋯ A n , n − 1 A n n ) A^{*}= \left(\begin{array}{ccccc} A_{11} & A_{21} & \cdots & A_{n-1,1} & A_{n 1} \\ A_{12} & A_{22} & \cdots & A_{n-1,2} & A_{n 2} \\ \vdots & \vdots & & \vdots & \vdots \\ A_{1, n-1} & A_{2, n-1} & \cdots & A_{n-1, n-1} & A_{n-1, n} \\ A_{1 n} & A_{2, n} & \cdots & A_{n, n-1} & A_{n n} \end{array}\right) A∗= A11A12⋮A1,n−1A1nA21A22⋮A2,n−1A2,n⋯⋯⋯⋯An−1,1An−1,2⋮An−1,n−1An,n−1An1An2⋮An−1,nAnn
为矩阵A的伴随矩阵
性质
(
1
)
A
A
∗
=
A
∗
A
=
∣
A
∣
E
(
2
)
(
A
∗
)
−
1
=
(
A
−
1
)
∗
=
1
∣
A
∣
A
(
∣
A
∣
≠
0
)
(
3
)
(
k
A
)
∗
=
k
n
−
1
A
∗
(
4
)
(
A
∗
)
T
=
(
A
T
)
∗
(
5
)
∣
A
∗
∣
=
∣
A
∣
n
−
1
(
6
)
(
A
∗
)
∗
=
∣
A
∣
n
−
2
A
(
n
⩾
2
)
\begin{array}{l} (1)\ {A A^{*}}=A^{*} A=|A| E \\(2)\ \left(A^{*}\right)^{-1}=\left(A^{-1}\right)^{*}=\frac{1}{|A|} A \quad(|A| \neq 0) \\(3)\ (k A)^{*}=k^{n-1} A^{*} \\(4) \ \left(A^{*}\right)^{\mathrm{T}}=\left(A^{\mathrm{T}}\right)^{*} \\(5) \ \left|A^{*}\right|=|A|^{n-1} \\(6) \ \left(A^{*}\right)^{*}=|A|^{n-2} A \quad(n \geqslant 2) \end{array}
(1) AA∗=A∗A=∣A∣E(2) (A∗)−1=(A−1)∗=∣A∣1A(∣A∣=0)(3) (kA)∗=kn−1A∗(4) (A∗)T=(AT)∗(5) ∣A∗∣=∣A∣n−1(6) (A∗)∗=∣A∣n−2A(n⩾2)
性质1的证明:

证明
(
3
)
A
A
∗
=
∣
A
∣
E
,
∣
A
∣
∣
A
∗
∣
=
∣
∣
A
∣
E
∣
=
∣
A
∣
n
,
∣
A
∗
∣
=
∣
A
∣
n
−
1
(
6
)
(
A
∗
)
∗
=
∣
A
∗
∣
(
A
∗
)
−
=
∣
A
∣
n
−
1
(
∣
A
∣
A
−
1
)
−
1
=
∣
A
∣
n
−
2
A
(3) \ AA^* = |A|E, |A||A^*| = | |A|E | = |A|^{n},|A^*| = |A|^{n-1} \\ (6) \quad (A^*)^* = |A^*|(A^*)^{-} = |A|^{n-1}(|A|A^{-1})^{-1} = |A|^{n-2}A
(3) AA∗=∣A∣E,∣A∣∣A∗∣=∣∣A∣E∣=∣A∣n,∣A∗∣=∣A∣n−1(6)(A∗)∗=∣A∗∣(A∗)−=∣A∣n−1(∣A∣A−1)−1=∣A∣n−2A
二 运算及性质
加减

运算法则

乘法
定义(A的列数要与B的行数相同才能进行相乘)

运算

数乘

运算法则

转置
定义

矩阵多项式

重要性质
- $ \left(\boldsymbol{A}{\mathrm{T}}\right){\mathrm{T}}=\boldsymbol{A} $
- $ (k \boldsymbol{A})^{\mathrm{T}}=k \boldsymbol{A}^{\mathrm{T}} $
- $ \left(\boldsymbol{A}{-1}\right){\mathrm{T}}=\left(\boldsymbol{A}{\mathrm{T}}\right){-1} $
- $ \left(\boldsymbol{A}{\mathrm{T}}\right){m}=\left(\boldsymbol{A}{m}\right){\mathrm{T}} $
- $ (\boldsymbol{A} \pm \boldsymbol{B}){\mathrm{T}}=\boldsymbol{A}{\mathrm{T}} \pm \boldsymbol{B}^{\mathrm{T}} $
- $ (\boldsymbol{A} \boldsymbol{B}){\mathrm{T}}=\boldsymbol{B}{\mathrm{T}} \boldsymbol{A}^{\mathrm{T}} $
补充
( 1 ) A ≠ 0 , B ≠ 0 , 无法推出 A B ≠ 0 (1)\ A \neq 0,B \neq 0, 无法推出 AB \neq 0 (1) A=0,B=0,无法推出AB=0,同理AB=0也无法推出A=0或B=0
( 2 ) A ≠ 0 , 无法推出 A k ≠ 0 (2)\ A \neq 0, 无法推出 A^k \neq 0 (2) A=0,无法推出Ak=0
( 3 ) A x = λ x 特征值 , 有 f ( A ) x = f ( λ ) x (3)\ Ax=\lambda x \ 特征值 ,有f(A)x = f(\lambda)x (3) Ax=λx 特征值,有f(A)x=f(λ)x
( 4 ) A B = A ( β 1 , β 2 ) = ( α 1 , α 2 ) B (4)AB = A(\beta_1,\beta2) = (\alpha_1,\alpha_2)B (4)AB=A(β1,β2)=(α1,α2)B
( 5 ) A 2 − A − 6 E = ( A + 2 E ) ( A − 3 E ) (5)A^2-A-6E = (A+2E)(A-3E) (5)A2−A−6E=(A+2E)(A−3E)
( 6 ) 若 A B = B A ,则 ( A B ) 2 = ( B A ) 2 (6) 若AB=BA,则(AB)^2 = (BA)^2 (6)若AB=BA,则(AB)2=(BA)2
( 7 ) 若 C = A B ,则说明 C 的列向量可由 A 的列向量表示, r ( A , C ) = r ( A ) (7) 若C=AB,则说明C的列向量可由A的列向量表示,r(A,C) = r(A) (7)若C=AB,则说明C的列向量可由A的列向量表示,r(A,C)=r(A)
注意:矩阵的乘法交换律不一定成立【如AB 不一定等于BA】;矩阵有零因子;矩阵没有消去律。
三 矩阵的逆
背景

3.1 定义
类比一个数的倒数乘以该数,值为1

注意:若矩阵A可逆则对应的逆矩阵是唯一的。若A可逆,由AB=AC可推出B=C,当A不可逆时候不一定。
3.2 逆阵定理
设A为nxn矩阵,则下列命题是等价的,即对某一特定的矩阵A,它们同时为真或同时为假。
a. A 是可逆矩阵. b. A 行等价于 n × n 单位矩阵. c. A 有 n 个主元位置. d. 方程 A x = 0 仅有平凡解. 即零解 e. A 的各列线性无关. f. 线性变换 x ↦ A x 是一对一的. g. 对 R n 中任意 b , 方程 A x = b 至少有一个解 h. A 的各列生成 R n . i. 线性变换 x ↦ A x 把 R n 映上到 R n . j. 存在 n × n 矩阵 C 使 C A = I . k. 存在 n × n 矩阵 D 使 A D = I . l. A ⊤ 是可逆矩阵. m. ∣ A ∣ ≠ 0 n. A 为若干初等阵之积 \begin{array}{l}\text { a. } A \text { 是可逆矩阵. } \\ \text { b. } A \text { 行等价于 } n \times n \text { 单位矩阵. } \\ \text { c. } A \text { 有 } n \text { 个主元位置. } \\ \text { d. 方程 } A \boldsymbol{x}=\boldsymbol{0} \text { 仅有平凡解. 即零解} \\ \text { e. } A \text { 的各列线性无关. } \\ \text { f. 线性变换 } \boldsymbol{x} \mapsto A \boldsymbol{x} \text { 是一对一的. } \\ \text { g. 对 } \mathbb{R}^{n} \text { 中任意 } \boldsymbol{b}, \text { 方程 } A \boldsymbol{x}=\boldsymbol{b} \text { 至少有一个解 } \\ \text { h. } A \text { 的各列生成 } \mathbb{R}^{n} \text {. } \\ \text { i. 线性变换 } \boldsymbol{x} \mapsto A \boldsymbol{x} \text { 把 } \mathbb{R}^{n} \text { 映上到 } \mathbb{R}^{n} . \\ \text { j. 存在 } n \times n \text { 矩阵 } C \text { 使 } C A=I . \\ \text { k. 存在 } n \times n \text { 矩阵 } D \text { 使 } A D=I . \\ \text { l. } A^{\top} \text { 是可逆矩阵. } \\ \text { m. } |A| \neq 0 \\ \text { n. } A 为若干初等阵之积 \end{array} a. A 是可逆矩阵. b. A 行等价于 n×n 单位矩阵. c. A 有 n 个主元位置. d. 方程 Ax=0 仅有平凡解. 即零解 e. A 的各列线性无关. f. 线性变换 x↦Ax 是一对一的. g. 对 Rn 中任意 b, 方程 Ax=b 至少有一个解 h. A 的各列生成 Rn. i. 线性变换 x↦Ax 把 Rn 映上到 Rn. j. 存在 n×n 矩阵 C 使 CA=I. k. 存在 n×n 矩阵 D 使 AD=I. l. A⊤ 是可逆矩阵. m. ∣A∣=0 n. A为若干初等阵之积
证明命题m
充分性
∵
∣
A
∣
!
≠
0
∴
A
A
∗
=
∣
A
∣
E
,
A
1
∣
A
∣
A
∗
=
E
,
A
−
1
=
1
A
A
∗
必要性
∵
A
可逆
∴
存在
B
A
=
E
,
∣
B
∣
∣
A
∣
=
1
,
可得
∣
A
∣
≠
0
充分性 \because |A|! \neq 0 \therefore AA^* = |A|E,A\frac{1}{|A|}A^* = E,A^{-1} = \frac{1}{A}A^{*} \\ 必要性 \because A可逆 \therefore 存在BA = E,|B||A|=1,可得|A| \neq 0
充分性∵∣A∣!=0∴AA∗=∣A∣E,A∣A∣1A∗=E,A−1=A1A∗必要性∵A可逆∴存在BA=E,∣B∣∣A∣=1,可得∣A∣=0
证明a-l:

3.3 性质
简单抽象矩阵的逆阵可假设为【x11,x12;x21,x22】
1. ( A − 1 ) − 1 = A . 2. ( k A ) − 1 = 1 k A − 1 . 3. ( A B ) − 1 = B − 1 A − 1 . 4. ( A T ) − 1 = ( A − 1 ) T . 5. ( A n ) − 1 = ( A − 1 ) n . 6. 设 A , B 分别为 m 利 n 阶可逆矩阵,则 (1) ( A O O B ) − 1 = ( A − 1 O O B − 1 ) ; (2) ( O A B O ) − 1 = ( O B − 1 A − 1 O ) (3) ( A C O B ) − 1 = ( A − 1 − A − 1 C B − 1 O B − 1 ) \begin{array}{l} \text { 1. }\left(\boldsymbol{A}^{-1}\right)^{-1}=\boldsymbol{A} . \\ \text { 2. }(k \boldsymbol{A})^{-1}=\frac{1}{k} \boldsymbol{A}^{-1} . \\ \text { 3. }(\boldsymbol{A} \boldsymbol{B})^{-1}=\boldsymbol{B}^{-1} \boldsymbol{A}^{-1} . \\ \text { 4. }\left(\boldsymbol{A}^{\mathrm{T}}\right)^{-1}=\left(\boldsymbol{A}^{-1}\right)^{\mathrm{T}} \text {. } \\ \text { 5. }\left(\boldsymbol{A}^{n}\right)^{-1}=\left(\boldsymbol{A}^{-1}\right)^{n} . \\ \text { 6. 设 } \boldsymbol{A}, \boldsymbol{B} \text { 分别为 } m \text { 利 } n \text { 阶可逆矩阵,则 } \\ \begin{array}{ll} \text { (1) }\left(\begin{array}{ll}\boldsymbol{A} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{B}\end{array}\right)^{-1}=\left(\begin{array}{cc}\boldsymbol{A}^{-1} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{B}^{-1}\end{array}\right) ; & \\ \text { (2) }\left(\begin{array}{ll}\boldsymbol{O} & \boldsymbol{A} \\ \boldsymbol{B} & \boldsymbol{O}\end{array}\right)^{-1}=\left(\begin{array}{cc}\boldsymbol{O} & \boldsymbol{B}^{-1} \\ \boldsymbol{A}^{-1} & \boldsymbol{O} \end{array}\right) & \\ \text { (3) }\left(\begin{array}{ll}\boldsymbol{A} & \boldsymbol{C} \\ \boldsymbol{O} & \boldsymbol{B}\end{array}\right)^{-1}=\left(\begin{array}{cc}\boldsymbol{A^{-1}} & \boldsymbol{-A^{-1}CB^{-1}} \\ \boldsymbol{O} & \boldsymbol{B^{-1}} \end{array}\right) \end{array} \end{array} 1. (A−1)−1=A. 2. (kA)−1=k1A−1. 3. (AB)−1=B−1A−1. 4. (AT)−1=(A−1)T. 5. (An)−1=(A−1)n. 6. 设 A,B 分别为 m 利 n 阶可逆矩阵,则 (1) (AOOB)−1=(A−1OOB−1); (2) (OBAO)−1=(OA−1B−1O) (3) (AOCB)−1=(A−1O−A−1CB−1B−1)
三种运算:*、T、-1是可交换的
证明6(3)
(
A
C
O
B
)
(
x
11
x
12
x
21
x
22
)
=
E
B
X
21
=
0
,
X
21
=
0
B
X
22
=
E
,
X
22
=
B
−
1
A
X
11
+
C
X
21
=
E
,
X
11
=
A
−
1
A
X
12
+
C
X
22
=
0
,
A
−
A
X
12
=
−
A
−
1
C
B
−
1
\left(\begin{array}{ll}\boldsymbol{A} & \boldsymbol{C} \\ \boldsymbol{O} & \boldsymbol{B}\end{array}\right) \left(\begin{array}{cc}\boldsymbol{x_{11}} & \boldsymbol{x_{12}} \\ \boldsymbol{x_{21}} & \boldsymbol{x_{22}} \end{array}\right) = E \\ BX_{21}=0,X_{21}=0\\ BX_{22}=E,X_{22}=B^{-1}\\ AX_{11}+CX_{21}=E,X_{11}=A^{-1}\\ AX_{12}+CX_{22}=0,A^{-}AX_{12}=-A^{-1}CB^{-1}\\
(AOCB)(x11x21x12x22)=EBX21=0,X21=0BX22=E,X22=B−1AX11+CX21=E,X11=A−1AX12+CX22=0,A−AX12=−A−1CB−1
3.4 逆阵求解
一般不使用方法一,但是可以使用该公式的逆求伴随矩阵。
紧抓定义式:B * B的逆 = E

初等变换法中即可行变换、也可列变换
伴随矩阵法
运算量大
例题:

初等变换法
把A变换为E的过程,每一次变换相当于初等变换,累积起来就相当于A的逆。
证明:

例题:

拼凑法
这一类问题为已知关于矩阵A的某个式子,求(A+kE)的逆,思路是拼凑出 (A+kE) ( 拼凑 ) = E,从而可得(A+kE)的逆。拼凑时候要出现题目给出的已知条件。 1 − b n = ( 1 − b ) ( 1 + b + b 2 + . . . b n − 1 ) 1-b^n = (1-b)(1+b+b^2+...b^{n-1}) 1−bn=(1−b)(1+b+b2+...bn−1)
【例】 A 2 + A − 4 E = 0 , 求 ( A − E ) 的逆 A^2+A-4E=0,求(A-E)的逆 \quad A2+A−4E=0,求(A−E)的逆
【解】 ( A − E ) ( A + 2 E ) = 2 E , 从而 ( A − E ) − = 1 2 ( A + 2 E ) (A-E)(A+2E) = 2E,从而(A-E)^- = \frac{1}{2}(A+2E) (A−E)(A+2E)=2E,从而(A−E)−=21(A+2E)
matlab
a=[1 2 3;4 5 6; 7 8 9]
inv(a)
3.5 类单位阵的逆
对角矩阵的逆
[
a
1
a
2
a
3
]
−
1
=
[
1
a
1
1
a
2
1
a
3
]
\left[\begin{array}{lll}a_{1} & & \\ & a_{2} & \\ & & a_{3}\end{array}\right]^{-1}=\left[\begin{array}{lll}\frac{1}{a_{1}} & & \\ & \frac{1}{a_{2}} & \\ & & \frac{1}{a_{3}}\end{array}\right]
a1a2a3
−1=
a11a21a31
类E矩阵的逆,把对角元素的位置改为1/k,再根据式子补充。
[ 2 − 1 0 1 ] − 1 = [ 1 2 1 0 1 ] \begin{bmatrix} 2 & -1 \\ 0 & 1 \end{bmatrix}^{-1} = \begin{bmatrix} \frac{1}{2} & 1 \\ 0 & 1 \end{bmatrix} [20−11]−1=[21011]
反单位阵+仅1个其他位置元素,则其逆为对称位置的值添加负号(仅适用于奇数阶+仅一个位置元素更改)。
[ 0 2 1 0 1 0 1 0 0 ] − 1 = [ 0 0 1 0 1 0 1 − 2 0 ] \begin{bmatrix} 0 & 2 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{bmatrix}^{-1} = \begin {bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & -2 & 0 \end{bmatrix} 001210100 −1= 00101−2100
初等变换的E型阵逆阵是它变换的负数(思考,列变换)
E i , j − 1 ( k ) = E i , j ( − k ) E^{-1}_{i,j}(k)=E_{i,j}(-k) Ei,j−1(k)=Ei,j(−k)
只对换行或列的E型阵的逆是它本身(思考,行变换)
E ( i , j ) 2013 E ( i , j ) = E E^{2013}_{(i,j)}E_{(i,j)} = E E(i,j)2013E(i,j)=E
3.6 证明可逆
不可逆:|A| = -|A| = 0
四 初等变换
方程组的以下三种变形称为方程组的同解变形
(1)对调两个方程;
(2)某个方程两边同乘以一个非零常数;
(3)某个方程的倍数加到另一个方程
(4)代参数时候注意不能把0为这个可能性约分
4.1 行变换
E(i,j)(k)第j行的k倍加到i行,左乘
(1)对调矩阵的两行;
(2)矩阵的某行乘以非零常数k;
(3)矩阵某行的倍数加到另一行
4.2 列变换
E(i,j)(k)第i列的k倍加到j列,右乘
(1)对调矩阵的两列;
(2)矩阵某列乘以非零常数k;
(3)矩阵某列的倍数加到另一列
矩阵的初等行变换和初等列变换统称为矩阵的初等变换
4.3 初等矩阵
由单位矩阵经一次初等变换得到的矩阵称为初等矩阵,们分别是
| 变换名称 | 符号 | 作用 |
|---|---|---|
| 倍乘初等矩阵 | E(i(k)) | E的第i行(或第i列)乘以k倍 |
| 互换初等矩阵 | E(i,j) | E的第i、j行(列)互换 |
| 倍加初等矩阵 | E(ij(k)) | E的第j行(或i列)的k倍加到第i行(j列) |
注意:左乘 行变换;右乘 列变换。关于Eij有一些书籍的ij可能是相反的。下面LU分解中的Eij以该处为准。
仅经过行变换Q,无法保证可把矩阵A转换为 = ( Er 0 0 0 ) =\left(\begin{array}{cc}\text { Er } & 0 \\ 0 & 0\end{array}\right) =( Er 000),因为行上下加减只能把下变为0;仅经过列变换P只能把右变为0;因此,如果行、列变换都进行,QAP(Q,P均可逆),则可以把A转换为 = ( Er 0 0 0 ) =\left(\begin{array}{cc}\text { Er } & 0 \\ 0 & 0\end{array}\right) =( Er 000)
五 矩阵的秩
更详细的内容请参阅线性代数及其应用第二章及子空间内容
5.1 定义
定义1 类似极大线性无关组

定义2
矩阵A的秩(记为rank A)是A的列空间的维数.
5.2 求法
求法1

求法2 行变换阶梯化,非零行的个数

5.3 性质
证明性质(1)(同解的线性方程组,秩相等)
A
X
=
0
,
A
T
A
X
=
0
A
T
A
X
=
0
,
X
T
A
T
A
X
=
(
A
T
)
T
A
X
=
0
即
A
X
=
0
,
所以
A
A
T
A
同解
,
故秩相等
AX=0,A^TAX=0 \\ A^TAX = 0, X^TA^TAX=(AT)^TAX=0 \\ 即AX=0,所以A A^TA 同解,故秩相等
AX=0,ATAX=0ATAX=0,XTATAX=(AT)TAX=0即AX=0,所以AATA同解,故秩相等
(1)$r ( A ) = r ( A ^ { T } ) = r ( A ^ { T } A ) $
(2)当 k ≠ 0 k \neq 0 k=0时 r ( k A ) = r ( A ) r ( kA ) = r ( A ) r(kA)=r(A)
(3) r ( A ± B ) ≤ r ( A ) + r ( B ) , m a x ( r ( A ) , r ( B ) ) ≤ r ( A , B ) ≤ r ( A ) + r ( B ) r ( A \pm B ) \leq r ( A ) + r ( B ) ,max(r(A),r(B)) \le r(A,B) \le r(A)+r(B) r(A±B)≤r(A)+r(B),max(r(A),r(B))≤r(A,B)≤r(A)+r(B)
(4) r ( C ) = r ( A B ) ≤ m i n ( r ( A ) , r ( B ) ) 、 r ( C ) ≤ r ( A ) r ( C ) ≤ r ( B ) ? r(C) = r ( AB ) \leq min ( r ( A ) , r ( B ) )、r(C) \leq r(A) r(C) \leq r(B)? r(C)=r(AB)≤min(r(A),r(B))、r(C)≤r(A)r(C)≤r(B)?
(5)若 A A A可逆,则 r ( A B ) = r ( B ) , r ( B A ) = r ( B ) r ( AB ) = r ( B ) , r ( BA ) = r ( B ) r(AB)=r(B),r(BA)=r(B)
(6)若 A A A是 m × n m \times n m×n矩阵, B B B是 n × s n \times s n×s矩阵, A B = O AB = O AB=O则 r ( A ) + r ( B ) ≤ n r ( A ) + r ( B ) \leq n r(A)+r(B)≤n
(7) r [ A 0 0 B ∣ = r ( A ) + r ( B ) r [ \begin{array} { ll } { { A } } & { { 0 } } \\ { { 0 } } & { { B } } \\ \end{array} | = {r ( A )} + {r ( B )} r[A00B∣=r(A)+r(B)、 r [ A A B 0 B ∣ = r ( A ) + r ( B ) r [ \begin{array} { ll } { { A } } & { { AB } } \\ { { 0 } } & { { B } } \\ \end{array} | = {r ( A )} + {r ( B )} r[A0ABB∣=r(A)+r(B)(通过列变换可消去AB(a_1+a_2,a_2+a_1),而B由于左侧是0阵,不受影响;BA就未必了,无法消去), r ( A , A B ) = r ( A ) , r ( A , B A ) ≥ r ( A ) r(A,AB) = r(A),r(A,BA) \ge r(A) r(A,AB)=r(A),r(A,BA)≥r(A)
(8)若 A ∼ B A \sim B A∼B则 r ( A ) = r ( B ) , r ( A + k E ) = r ( B + k E ) r ( A ) = r ( B ) , r ( A + kE ) = r ( B + kE ) r(A)=r(B),r(A+kE)=r(B+kE)
(9) r ( A ∗ ) = { n , 如果 r ( A ) = n , 1 , 如果 r ( A ) = n − 1 , 0 , 如果 r ( A ) < n − 1. ( n ≥ 2 ) r\left(\boldsymbol{A}^{*}\right)=\left\{\begin{array}{ll}n, & \text { 如果 } r(\boldsymbol{A})=n, \\ 1, & \text { 如果 } r(\boldsymbol{A})=n-1, \\ 0, & \text { 如果 } r(\boldsymbol{A})<n-1 .\end{array}\right. (n \ge 2) r(A∗)=⎩ ⎨ ⎧n,1,0, 如果 r(A)=n, 如果 r(A)=n−1, 如果 r(A)<n−1.(n≥2)
(10) r ( A ) = 1 的充要条件是存在 α 和 β ≠ 0 , 使得 A = α β T r(A) = 1 的充要条件是 存在 \alpha 和 \beta \neq 0,使得A=\alpha \beta ^T r(A)=1的充要条件是存在α和β=0,使得A=αβT(默认是列向量,展开后其他行都是第一行的倍数)
(11) r ( A ) = 1 , A n = k n − 1 A , 其中 k = α β T = ∑ a i i = ∑ λ i r(A) = 1,A^n = k^{n-1}A,其中k=\alpha \beta ^T=\sum a_{ii} =\sum \lambda_{i} r(A)=1,An=kn−1A,其中k=αβT=∑aii=∑λi
(12) 矩阵的r=m,则任意的m+1阶子式的行列式均为0
证明性质(9) M_{ij}:n-1阶子式
∵
r
(
A
)
=
n
,
∣
A
∣
≠
0
,
∣
A
∗
∣
=
∣
A
∣
n
−
1
≠
0
∴
r
(
A
∗
)
=
n
∵
r
(
A
)
=
n
−
1
,
A
A
∗
=
0
,
r
(
A
)
+
r
(
A
∗
)
≤
n
,
r
(
A
∗
)
≤
1
又
∵
存在
M
i
j
≠
0
,则
A
∗
不是
0
阵,
r
(
A
∗
)
≥
1
∴
r
(
A
∗
)
=
1
∵
r
(
A
)
<
n
−
1
∴
M
i
j
=
0
,
r
(
A
∗
)
=
0
\because r(A) = n,|A|\neq0,|A*|=|A|^{n-1} \neq 0 \ \therefore r(A^*)=n \\ \because r(A) = n-1, AA^*=0,r(A)+r(A^*) \le n,r(A^*) \le 1 \\ 又\because 存在M_{ij} \neq 0, 则A^*不是0阵,r(A^*) \ge 1 \therefore r(A^*) = 1 \\ \because r(A)<n-1 \therefore M_{ij}=0,r(A^*)=0
∵r(A)=n,∣A∣=0,∣A∗∣=∣A∣n−1=0 ∴r(A∗)=n∵r(A)=n−1,AA∗=0,r(A)+r(A∗)≤n,r(A∗)≤1又∵存在Mij=0,则A∗不是0阵,r(A∗)≥1∴r(A∗)=1∵r(A)<n−1∴Mij=0,r(A∗)=0
秩的本质是方程组约束条件的个数


矩阵等价QAP=B 则其 充要条件 r(A) = r(B)
列向量的秩等于0或1(当a是0向量时候秩才为0)
α ⊤ α = ( a 1 … a n ) ∣ a 1 ⋮ a n ∣ = a 1 2 + ⋯ + a n 2 = ∣ α ∣ 2 ≥ 0 \alpha^{\top} \alpha=\left(a_{1} \ldots a_{n}\right)\left|\begin{array}{c}a_{1} \\ \vdots \\ a_{n}\end{array}\right|=a_{1}^{2}+\cdots+a_{n}^{2}=|\alpha|^{2}\ge 0 α⊤α=(a1…an) a1⋮an =a12+⋯+an2=∣α∣2≥0
【例题】2021数一

六 分块矩阵
思想:矩阵可以看作是一个数的矩形表,也可以把它看作一组列向量。
6.1 定义
将矩阵用若干纵线和横线分成许多小块,每一小块称为原矩阵的子矩阵(或子块),把子块看成原矩阵的一个元素,则原矩阵叫分块矩阵
6.2 运算
加法

乘法


其他
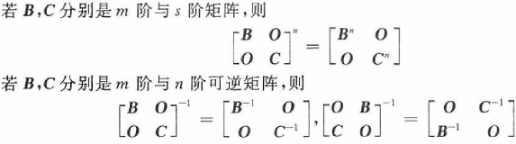
[ A B C D ] T = [ A T C T B T D T ] \left[\begin{array}{ll}\boldsymbol{A} & \boldsymbol{B} \\ \boldsymbol{C} & \boldsymbol{D}\end{array}\right]^{\mathrm{T}}=\left[\begin{array}{ll}\boldsymbol{A}^{\mathrm{T}} & \boldsymbol{C}^{\mathrm{T}} \\ \boldsymbol{B}^{\mathrm{T}} & \boldsymbol{D}^{\mathrm{T}}\end{array}\right] [ACBD]T=[ATBTCTDT]
七 矩阵因式分解
思想
- 矩阵乘法是数据的综合,矩阵因式分解是数据的分解
- 矩阵因式分解把矩阵表示为多个矩阵的乘积。
- 计算机中称之为对A数据的预处理,该结构或许更有利与分析,可能更利于计算。
7.1 LU分解
在研究如何构造LU之前,我们看看它的作用。当A=LU,方程Ax=b可以写为L(Ux) = b,令Ux=y,则Ly=b,Ux=y。由于L,U均为三角矩阵,因此求解较为容易。
LU分解算法

7.2 分解实例
题目:

解:

这里需要注意一下,单位矩阵基础上增加某个位置元素值为k,那么其对应的逆矩阵就是单位矩阵加该位置的-k。
例如L21=-2其实是E21(2)的"逆",意为把第一行的2倍加到第二行,由矩阵A可以看出,其实就相当于 -4+2*(2)=0
LU分解在数值计算中的作用

八 其他
8.1 方阵行列式

8.2 其他
进阶阅读书籍
| 名称 | 难度 |
|---|---|
| MIT的线代课 | |
| 线性代数及其应用 | 入门 |
| 3Blue1blown的线性代数本质系列 |
九 基础例题
AA*=|A|E
9.1 矩阵运算
逆的关系

解:
若
A
B
C
=
E
则
A
−
1
=
B
C
或
A
B
=
C
−
1
有
A
−
1
A
=
B
C
A
=
E
或
C
C
−
1
=
C
A
B
=
E
若\ ABC = E \\ 则\ A^{-1} = BC或AB=C^{-1} \\ 有\ A^{-1}A=BCA=E或CC^{-1}=CAB=E
若 ABC=E则 A−1=BC或AB=C−1有 A−1A=BCA=E或CC−1=CAB=E
分解后发现即证明AB=BA,利用题目信息左乘右乘共4仲,对比式子

- 方阵的行列式

9.2 幂矩阵

法二
矩阵
A
1
的作用:
1.
第一行乘以倍数
1
2.
E
12
(
1
)
:
第二行的
1
倍加到第一行
3.
第二行乘以倍数
2
显然
A
n
中
a
11
=
a
22
=
2
n
,
a
21
=
0
A
2
2
×
1
+
2
1
A
3
2
×
[
2
×
1
+
2
1
]
+
2
2
A
4
2
×
[
2
×
[
2
×
1
+
2
1
]
+
2
2
]
+
2
3
A
n
2
×
[
2
×
[
2
×
[
2.
[
.
[
.
[
2
×
1
+
2
1
]
+
2
2
]
+
2
3
]
.
]
.
.
.
+
2
n
−
2
]
+
2
n
−
1
=
2
n
−
1
+
2
n
−
1
+
2
n
−
1
+
.
.
.
.
.
.
.
.
.
+
2
n
−
1
=
n
×
2
n
−
1
=
C
n
1
×
2
n
−
1
感觉有点像秦九韶
由此可得
A
1
n
=
[
2
n
C
n
1
2
n
−
1
0
2
n
]
\begin{align} &矩阵A_1的作用:\\ & 1.\ 第一行乘以倍数1 \\ & 2.\ E_{12}(1):第二行的1倍加到第一行\\ & 3.\ 第二行乘以倍数2 \\ & 显然A^{n}中a_{11}=a_{22}=2^n,a_{21}=0 \\ & A^2 \quad 2\times1+2^1 \\ & A^3 \quad 2\times[2\times1+2^1]+2^2 \\ & A^4 \quad 2\times[2\times[2\times1+2^1]+2^2]+2^3 \\ & A^n \quad 2\times[2\times[2\times[2.[.[.[2\times1+2^1]+2^2]+2^3].]...+2^{n-2}]+2^{n-1}\\ & \ \quad = 2^{n-1}+2^{n-1}+2^{n-1}+.........+2^{n-1} \\ & \ \quad = n \times 2^{n-1} = C_n^1 \times 2^{n-1} \\ & 感觉有点像秦九韶 \\ & 由此可得A_1^n = \begin{bmatrix} 2^n & C_n^1 2^{n-1}\\ 0 & 2^n \end{bmatrix} \end{align}
矩阵A1的作用:1. 第一行乘以倍数12. E12(1):第二行的1倍加到第一行3. 第二行乘以倍数2显然An中a11=a22=2n,a21=0A22×1+21A32×[2×1+21]+22A42×[2×[2×1+21]+22]+23An2×[2×[2×[2.[.[.[2×1+21]+22]+23].]...+2n−2]+2n−1 =2n−1+2n−1+2n−1+.........+2n−1 =n×2n−1=Cn1×2n−1感觉有点像秦九韶由此可得A1n=[2n0Cn12n−12n]
- P[] = AP,因此P-1AP = []
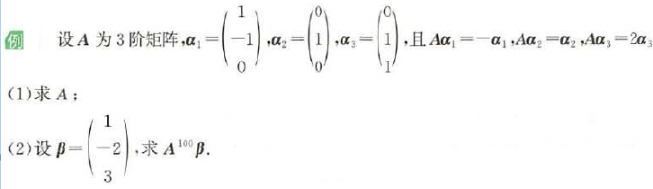
解:P的逆,E(21)(1),E(23)(-1)P = E




解(2)P[A|E] = [PA | P] = [B | P] E(12),E(31)(-2),E(23),E(32)(1),E(21)(1)

9.3 逆阵计算

- 证明一个矩阵可逆即证明该矩阵 [] 乘以某个矩阵 [] = E

- 拼凑



- 证明一个矩阵可逆,则找出它的逆或者证明其行列式不为0


- 求逆

9.4 A*与逆矩
紧抓公式 A* = |A|A-1


-
计算 A − 1 B 时候不需要把 A 的逆算出来,仅需 [ A ∣ B ] 变换为 [ A − 1 A ∣ A − 1 B ] = [ E ∣ A − 1 B ] 计算A^{-1}B时候不需要把A的逆算出来,仅需[A|B]变换为[A^{-1}A|A^{-1}B] = [E|A^{-1}B] 计算A−1B时候不需要把A的逆算出来,仅需[A∣B]变换为[A−1A∣A−1B]=[E∣A−1B]




- 类正单位阵的逆是它本身
A可逆,E(i,j)A = B,求A*与B*的关系
∵
E
(
i
,
j
)
A
=
B
,
∣
E
(
i
,
j
)
∣
∣
A
∣
=
−
∣
A
∣
=
∣
B
∣
∴
B
∗
=
∣
B
∣
B
−
1
=
−
∣
A
∣
A
−
1
E
(
i
,
j
)
−
1
=
−
A
∗
E
(
i
,
j
)
\because E(i,j)A = B,|E(i,j)||A| = -|A| = |B| \\ \therefore B^* = |B| B^{-1} = -|A| A^{-1}E(i,j)^{-1} =-A^{*}E(i,j)
∵E(i,j)A=B,∣E(i,j)∣∣A∣=−∣A∣=∣B∣∴B∗=∣B∣B−1=−∣A∣A−1E(i,j)−1=−A∗E(i,j)
9.6 秩的计算
- 若 AB = 0 则 r ( A ) + r ( B ) ⩽ n r(\boldsymbol{A})+r(\boldsymbol{B}) \leqslant n r(A)+r(B)⩽n



























 856
856

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








