MATLAB——multicuboid创建长方体

最新推荐文章于 2025-03-16 13:08:52 发布

不懂音乐的欣赏者

最新推荐文章于 2025-03-16 13:08:52 发布

阅读量5.7k

点赞数 1

分类专栏： Matlab 文章标签： MATLAB 长方体 multicuboid 几何体

Matlab 专栏收录该内容

9 篇文章

订阅专栏

本文介绍使用multicuboid函数创建复杂几何体的方法，包括嵌套和堆叠的长方体，单个长方体及空心立方体。通过不同参数组合，可创建由多个长方体单元组成的几何形状，适用于PDE模型。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

multicuboid

multicuboid

创建由几个立方体单元形成的几何体在页面中全部折叠

句法

gm = multicuboid(W，D，H)
gm = multicuboid(W，D，H，Name，Value)

描述

gm =multicuboid(W，D，H，Name，Value)通过组合几个立方体单元来创建几何体，即可以同时创建多个长方体，组成复杂的几何体。

坐标系

创建每个长方体时，多节点使用以下坐标系。
在这里插入图片描述

实例

gm = multicuboid(W，D，H，Name，Value)

相同高度的嵌套长方体

创建一个由三个相同高度的嵌套长方体组成的几何体，并在PDE模型中显示此几何体。

使用multicuboid函数创建几何体。生成的几何体由三个单元组成。

gm = multicuboid（[2 3 5]，[4 6 10]，3）

gm =
  DiscreteGeometry with properties:
       NumCells：3
       NumFaces：18
       NumEdges：36
    NumVertices：24

创建PDE模型

model = createpde

model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: []
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

在模型中包含几何体

model.Geometry = gm

model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: [1x1 DiscreteGeometry]
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

绘制几何图形

pdegplot(model,'CellLabels','on','FaceAlpha',0.5)

在这里插入图片描述

堆叠的长方体

创建一个由四个堆叠长方体组成的几何体，并在PDE模型中包含此几何体。

使用带有ZOffset参数的multicuboid函数创建几何。得到的几何形状由四个堆叠在彼此顶部的单元组成。

gm = multicuboid(5,10,[1 2 3 4],'ZOffset',[0 1 3 6])

gm = 
  DiscreteGeometry with properties:

       NumCells: 4
       NumFaces: 21
       NumEdges: 36
    NumVertices: 20

创建PDE模型

model = createpde

model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: []
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

在模型中包含几何体

model.Geometry = gm

model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: [1x1 DiscreteGeometry]
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

绘制几何图形。

pdegplot(model,'CellLabels','on','FaceAlpha',0.5)

在这里插入图片描述

单个长方体

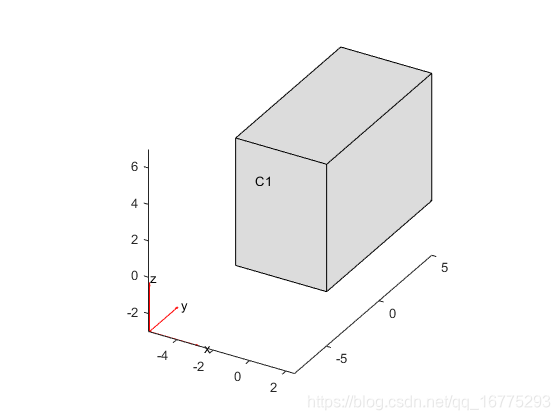
创建一个由单个长方体组成的几何体，并在PDE模型中包含此几何体。

使用multicuboid函数创建单个长方体。生成的几何体由一个单元组成。

gm = multicuboid(5,10,7)

gm = 
  DiscreteGeometry with properties:

       NumCells: 1
       NumFaces: 6
       NumEdges: 12
    NumVertices: 8

创建PDE模型

model = createpde

model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: []
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

在模型中包含几何体

model.Geometry = gm

model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: [1x1 DiscreteGeometry]
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

绘制几何图形。

pdegplot(model,'CellLabels','on')

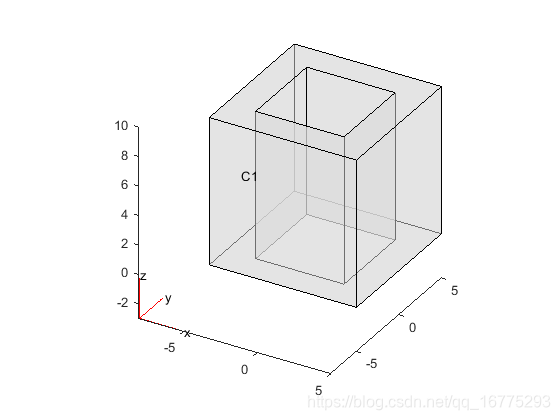
在这里插入图片描述

空心立方体

创建一个空心立方体并将其作为几何体包含在PDE模型中。

使用带有Void参数的multicuboid函数创建一个空心立方体。生成的几何体由一个单元组成。

gm = multicuboid([6 10],[6 10],10,'Void',[true,false])

gm = 
  DiscreteGeometry with properties:

       NumCells: 1
       NumFaces: 10
       NumEdges: 24
    NumVertices: 16

创建PDE模型。

model = createpde

model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: []
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

在模型中包含几何体。

model.Geometry = gm

model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: [1x1 DiscreteGeometry]
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

绘制几何图形。

pdegplot(model,'CellLabels','on','FaceAlpha',0.5)

在这里插入图片描述

输入参数

$W$ - 细胞宽度
正实数|矢量积极的实数
单元格宽度，指定为正实数或正实数的向量。如果W是向量，则W（i）指定第i个单元格的宽度。

宽度W，深度D和高度H可以是相同长度的标量或矢量。对于标量和矢量输入的组合，多节点将标量参数复制到相同长度的矢量中。

示例：

gm = multicuboid([1 2 3],[2.5 4 5.5],5)

$D$ - 细胞深度
正实数|矢量积极的实数
单元深度，指定为正实数或正实数的向量。如果D是向量，则D（i）指定第i个单元的深度。

宽度W，深度D和高度H可以是相同长度的标量或矢量。对于标量和矢量输入的组合，多节点将标量参数复制到相同长度的矢量中。

示例：
```
gm = multicuboid([1 2 3],[2.5 4 5.5],5)
```
$H$ - 细胞高度
正实数|矢量积极的实数
单元格高度，指定为正实数或正实数的向量。如果H是向量，则H（i）指定第i个单元的高度。

宽度W，深度D和高度H可以是相同长度的标量或矢量。对于标量和矢量输入的组合，多节点将标量参数复制到相同长度的矢量中。

示例：
```
gm = multicuboid(4,5,[1 2 3],'ZOffset',[0 1 3])
```
$N a m e$ - 值对参数
指定可选的逗号分隔的Name，Value参数对。 Name是参数名称，Value是对应的值。名称必须出现在引号内。您可以按任何顺序指定多个名称和值对参数，如Name1，Value1，…，NameN，ValueN。

示例：
```
gm = multicuboid([1 2],[1 2],[3 3],'Void',[true,false])
```
‘ZOffset’ - 每个单元的Z偏移量
0值的向量（默认值）|矢量的实数
每个单元格的Z偏移量，指定为实数向量。 ZOffset（i）指定第i个单元的Z偏移量。该向量必须与宽度向量W，深度向量D或高度向量H具有相同的长度。

示例：
```
gm = multicuboid(20,30,[10 10],'ZOffset',[0 10])
```
数据类型：双倍
$^{'} V o i d^{'}$ - 空单元格指示器
逻辑假值的向量（默认）|逻辑真值或假值的向量
空单元格指示符，指定为逻辑true或false值的向量。该向量必须具有与宽度向量W，深度向量D或高度向量H相同的长度。

值true对应于空单元格。默认情况下，multicuboid假定所有单元格都不为空。

示例：
```
gm = multicuboid([1 2],[1 2],[3 3],'Void',[true,false])
```
数据类型：双倍
输出参数
gm - 几何对象
DiscreteGeometry对象
几何对象，作为DiscreteGeometry属性对象返回。

限制

multicuboid允许您仅创建由堆叠或嵌套的长方体组成的几何。对于嵌套的长方体，几何体中的所有单元格的高度必须相同。对于堆叠长方体，几何体中的所有单元格的宽度和深度必须相同。使用ZOffset参数将单元格堆叠在一起而不重叠它们。
multicuboid不允许您创建相同宽度和深度的嵌套长方体。不支持调用多中心（w，d，[h1，h2，…]）。