
混沌无形
混沌系统是世界本质,无形之中存在规律。机器人智能化发展从线性过渡到混沌,本号将分享机器人全栈技术(感知、规划、控制;软件、机械、硬件等)。
43篇原创内容
公众号
[文末提供原文PDF免费下载(期刊论文版式)]
摘要:参数校准是机器人运动控制的基础,本文顺着从校准原理到具体实现方法的思路,详细阐述一般机器人驱动轮直径校准。
01

引言

当移动机器人机械本体设计、装配完成后,运动学方程也准备就绪,接下来就需要对机器人的各个参数进行校准,以提升机器人运动控制的精度。
这也是移动机器人参数校准系列文章的第一篇。
02

为什么要校准

在《常见移动机器人运动学模型》一文中总结了目前常见的移动机器人运动学模型,有了运动模型,便可将公式编写为代码进而实现机器人运动控制。
有实操经验的读者可能有所感触:机器人只是“大致”会按照我们发送的命令运动,但是运动精度并不高,尤其是运动距离较远,实际运动偏差就越大,最有可能的原因之一就是没有进行运动参数校准,就像以前的机械手表,每过一段时间,手表时间与实际时间就会产生偏差,我们就需要手动调节校准。
细数《常见移动机器人运动学模型》中的运动学方程,机器人中心速度最终会转化为驱动轮的线速度,也就是需要严格控制驱动轮按照设定的线速度运动,也就是需要严格控制电机输出轴按照设定转速转动,这点可设计闭环控制器来尽量保证,除此之外,还需要校准驱动轮的实际直径,这也是本文的讲解重点。
因此,只有保证驱动轮实际直径测量精准和电机输出轴转速准确才能有效保证驱动轮的线速度的准确度。
03

校准原理

校准一般是基于累计放大原理,并多次测量求平均。就如我们小学实验:准确测量一张纸的厚度是很困难的,所以就测量一摞纸的厚度,然后求平均,得到一张纸的厚度,通过叠加累计方式,降低测量误差。很多校准方法多采用此原理,只是具体实现方法有所区别。
而移动机器人轮直径校准采用的思想是:驱动轮转动一圈,测量运动过的路程,可将轮直径测量误差缩小π倍(C=πd,C和d分别表示圆周长、圆直径),若多滚动几圈,就可以将轮直径测量误差成倍缩小,所以直接控制机器人沿直线运动,让驱动轮转动N圈,测量驱动轮滚过的路程,便可以较为准确计算出轮直径。当然,理论上运动距离越远,校准精度越高。
04

轮直径校准分析

在进行轮直径校准之前,是需要(估计)测量一个粗糙的初始值的,可以使用游标卡尺等工具直接测量轮子的直径,以作为校准测量的初值,后续只需要在这个初值上加减就可以了。
不同构型的移动机器人的具体测量方法是有所区别的,本文分为以下两类进行讨论。
4.1
对称构型机器人
如图 4.1所示,这5类机器人机器人的构型是轴对称的,将这5种构型的机器人分为一类,是因为机器人前进直行速度方向(橘黄色箭头)与驱动轮滚动方向(灰色箭头)一致,而圆弧构型则不满足这种特点。

图 4.1 对称构型机器人. (a)两轮差速驱动机器人,(b)car-like robot,(c)四轮驱动机器人,(d)履带式机器人,(e)麦轮全向平台
如图 4.2所示,这里以两轮差速驱动机器人为例,讲解驱动轮直径校准的方法。
假设机器人以恒定速度沿直线前进一段距离后停下,因此理论上驱动轮应该转动的圈数N(不一定是整数),表示为
式中,_l_表示要行进的路程,_d_表示轮子的直径。
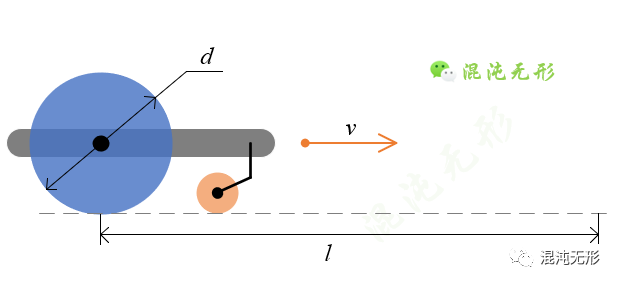
图 4.2 轮直径校准示意图.蓝色圆盘为驱动轮,浅黄色圆盘为万向轮.
所以,根据公式(1)可知,控制驱动轮旋转N圈,理论移动距离就应该为_lc_,但是由于未校准的驱动轮直径_d_0是通过直尺直接测量得到的,肯定不精确,所以实际运动距离_l_0肯定不是__lc__,存在一定的偏差B,表示为
式中,__lc__表示理论运动距离,_l_0表示实际运动距离,_d_0表示驱动轮直径初始测量值,_dc_表示驱动轮直径理论精确值。
而轮直径校准方法,就需要依据这个运动的偏差B来手动调整_d_0,尽量减小偏差B,当偏差B缩小趋近于0时,对应的_d_0也趋近于理论值了。
4.2
圆弧构型机器人

图 4.3 全向轮全向移动平台
与图 4.1中的对称构型机器人有所区别的是图 4.3中的全向轮移动平台,要校准全向轮直径的原理是一样的,但是计算细节要稍微变化一下,我们在《全向轮机器人运动模型及应用分析》一文中分析过:
当左下和右下两个轮子沿着前向等速滚动时,全向轮移动平台将沿着直线前向运动,如图 4.3所示,这里先分析右下轮与平台中心速度的关系,表示为
式中,_v_表示机器人几何中心的速度,_w_表示右下轮的轮毂角速度,_R_表示全向轮的半径,_v_∥表示右下轮的轮毂滚动速度,_θ_表示速度夹角。
进而可知,全向轮移动机器人直行运动过程中,全向轮的半径_R_可表示为
也可写为
其中,根据全向轮的几何构型关系,_θ_为30度,R’表示“等效半径”。
从公式(5)可以看出,将全向轮移动机器人视为“对称构型机器人”,则全向轮的“等效半径”就表示为_R_',也就转化为普通的“对称构型机器人”。
通过上述分析,结合公式(1)和(5)可知,
式中,_d_表示全向轮“等效”直径,含义与图 4.2中的轮直径一致。综上分析,可将全向轮移动平台的轮直径校准转化为章节4.1中对称构型机器人轮直径校准方法。
05

校准实验

5.1
实验思路分析
直接按照章节3中的原理,结合章节4中的公式换算,就可以间接测量出驱动轮直径,即:
控制机器人直线运动,并严格保证驱动轮转动_N_圈,并测量驱动轮移动的路程_l_(l>>d),便可计算出驱动轮直径,表示为
但是这样的测量方法存在个问题:如何严格控制机器人驱动轮转动_N_圈?
如果要实现准确控制驱动轮转动圈数,这里需要借助于安装在轮轴的编码器,用于测量驱动轮转动的圈数_M_,编写程序记录编码器读数增量达到M时,便控制电机停转,以此解决上述问题。
这里结合ROS官方提供的校准demo[1],介绍一种实际操作更方便的思路:
设定机器人直线运动校准距离__lc__,并使用直尺测量初始的驱动轮直径_d_0,因此对应的驱动轮转动的圈数_N_0,表示为
由于非常难以控制驱动轮整圈数转动,因此这里需要使用安装于轮轴的编码器辅助测量,假设驱动轮转动一整圈,编码器tick计数为_g_,则根据公式(8),得到编码器总tick计数_M_0为
这就可以控制机器人沿着直线运动,并保证编码器tick计数达到_M_0时,机器人立刻停止运动,所以实际上机器人真实运动距离_l_0为
公式(10)暗含的意思是:使用了驱动轮初始测量值_d_0计算得到的编码器tick计数_M_0,但机器人实际运动时,是真实的“精确直径的”驱动轮在运动,所以实际运动结果_l_0肯定不等于理论设定距离__lc__。
结果是不等于,要么是大于,要么是小于,这里分情况讨论:
假如实际运动距离大于理论设定距离(_l_0>lc),意思是实际运动距离超过了目标,这说明运动过远;运动过远的原因是公式(9)中计算的编码器tick计数_M_0大于实际真实值了;_M_0过大,是因为公式(9)中的使用直尺测量初始的驱动轮直径_d_0较真实直径_dc_偏小,所以应该适当增大_d_0,并重新计算_M_0,再次控制机器人运动进行测试。
反之(_l_0<lc),应该适当减小_d_0,并重新计算_M_0,再次控制机器人运动进行测试。
多次重复上述调整、实验,直到实际运动距离非常接近理论设定距离,所以适当提升直线运动校准距离__lc__,可有效提升校准精度。
而针对圆弧构型机器人,只需要在上述实验基础上,做好半径及编码器计数的转化即可。
5.2
具体(ROS)实现方法
如图 5.1所示,使用卷尺拉出一条长度2m的参考线段,然后控制机器人前向运动。
ROS官方提供的校准demo[1]还和章节图 5.1介绍的方法有细微区别:demo中使用了里程计(后续文章会讲解),机器人根据里程计来判断是否达到目标位置。

图 5.1 直线校准测试实验.黑色橡胶轮为驱动轮,卷尺拉伸长度2m.
这里简单概述里程计的原理:采集机器人左右差速轮的编码器计数及轮直径测量值,结合几何关系,就可以计算出机器人运动后的位置。
所以,可以进一步简化理解为:机器人自己认为达到目标位置时,就停下,而此时停下的位置很可能并不是真实的目标位置,这就需要通过调节驱动轮直径的数值,直到机器人能够准确达到目标位置为止。

在校准实验前,还应调节好驱动轮PID速度控制器的参数,保证能够“瞬间”启动、停止,以确保运动精度。

图 5.2 ROS节点网络
如图 5.2为轮直径校准实验对应的ROS网络节点图,其中calibrate_linear为校准节点,motor表示电机控制节点,odomsubpub为里程计发布节点。
其中,ROS校准demo还支持GUI调参,包括校准测试距离(test_distance)、运动速度(speed)、允许误差(tolerance)及里程计线性缩放校准因子(odom_linear_scale_correction)。

图 5.3 校准参数调节
参数调节及测试结果如表 5-1所示,反复调节,逐步收敛到较为理想的准确值,驱动轮的最终校准直径为252cm。
表 5-1 直线校准参数调节过程
| 轮直径/m | 0.26 | 0.24 | 0.25 | 0.255 | 0.252 |
|---|---|---|---|---|---|
| 理论距离/m | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 |
| 实际距离/m | 1.93 | 2.10 | 2.03 | 1.97 | 2.00 |
06

结论及展望

本文先阐述了参数校准的基本原理,并按照机器人构型的不同点分为两类,分别对对称型、圆弧型机器人进行了理论分析,提出校准思路,接着在从实用性角度提出改进的校准实验方法,最后结合ROS 校准demo阐述实验实现方法。
若要使用ROS校准demo,则需要根据其要求,自行编写好其配套程序;若不采用ROS demo,则可以直接驱动机器人直线运动一段距离,使用直尺测量,并记录编码器计数变化,以直接计算出实际的轮直径,还有其他各种实操方法,读者可自行设计实验。
(文章仅笔者个人分析,有误请指正,谢谢!)
参考资料
[1] https://github.com/turtlebot/turtlebot_apps/tree/indigo/turtlebot_calibration
福利放送
笔者为小伙伴们整理了期刊论文版式原文PDF,方便收藏和回味
链接:https://pan.baidu.com/s/194rE4epbhhXAQ_R14yaAfQ
提取码:520r
若链接失效,可在后台回复本文标题或发送邮件:Zippen-Huang@outlook.com
延伸阅读
-----------------------------------------------------------------------------
相关声明
1.如果转载本文,文末务必注明:“转自微信公众号:混沌无形”
2.若有侵权,请联系作者

全文完,感谢阅读!!如果觉得写的不错,那就点个赞或者“在看”吧。
混沌无形
混沌系统是世界本质,无形之中存在规律。机器人智能化发展从线性过渡到混沌,本号将分享机器人全栈技术(感知、规划、控制;软件、机械、硬件等)。
43篇原创内容
公众号

























 714
714

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










