最优加权最小二乘估计

Reference

• Matrix Differentiation
• 加权最小二乘法与局部加权线性回归
• 卡尔曼滤波与组合导航原理(1-2讲)

最小二乘估计

$Z=HX+V$
where, Z is the $m$ dimension observation vector; $X$ is a $n$ dimension state vector; $H$ is a $m\ast n$ matrix; $V$ is noise vector, $E(V)=0,Cov(V)=E(V{V}^T)=R$

优化方程如下
$min||Z-HX|{|}^2$

对$X$求导，令其结果为0, 求出$X$的最小方差估计

$\hat{X}=(H^{T}H{)}^{-1}{H}^{T}Z$

加权最小二乘估计

优化方程如下，相当与加入了信息矩阵（协方差矩阵的逆）
$min(Z-HX{)}^T{R}^{-1}(Z-HX)$

对$X$求导，令其结果为0, 求出$X$的最优估计
$\hat{X}=(H^T{R}^{-1}H{)}^{-1}{H}^T{R}^{-1}Z$

递推最小二乘法

分别对方差阵和状态估计进行递推，其实就是用上一时刻信息来表示当前状态的估计

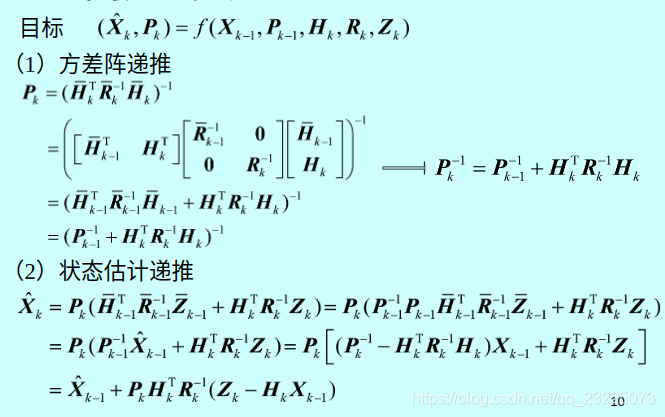
由于从$P_{k-1}$计算$P_k$需要求逆，这太烦了，利用矩阵求逆的公式。大概思路是，$A$是一个分块矩阵，写成两个三角阵的矩阵乘积，然后求inverse得到对应的求逆公式。