视觉slam14讲——第4讲李群李代数

最新推荐文章于 2024-07-28 01:41:04 发布

leeayu

最新推荐文章于 2024-07-28 01:41:04 发布

阅读量5.3k

点赞数 2

分类专栏：视觉slam14讲文章标签： SO3 SE3 sophus

本文链接：https://blog.csdn.net/qq_23225073/article/details/78348353

版权

视觉slam14讲专栏收录该内容

11 篇文章 18 订阅

订阅专栏

文章目录

1 基础
- 1.1 李群
- 1.2 李代数
2 李代数求导
3 李群与李代数习题

1 基础

1.1 李群

群是只有一种运算的集合,拥有四种性质.

封闭性
结合律
幺元
逆

比如, 特殊正交群和特殊欧氏群
这里写图片描述

李群指有连续光滑性质的群, SO(3)和SE(3)在实数空间上是连续的.

1.2 李代数

每个李群都有对应的李代数, 李代数描述了李群的局部性质.

李代数由一个集合,一和数域F, 一个二元运算 , 组成.
满足四条性质

封闭性
双线性
自反性
雅可比等价

李群SO(3)和SE(3)对应的李代数如下

这里写图片描述

李群SO(3)和SE(3)对应的李代数转换关系如下

2 李代数求导

有两种方法

用李代数表示姿态,然后根据李代数加法对李代数求导
对李群左乘或右乘微小扰动,然后对该扰动求导,称为左扰动模型和右扰动模型

使用Sophus库进行操作如下
(1) 构造李群SO(3)和SE(3)
以下三种方法都是等价的

/********************** SO3 **************************/
Eigen::Matrix3d R = Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d(0,0,1)).toRotationMatrix();// 沿Z轴转90度的旋转矩阵
Sophus::SO3 SO3_R(R);// Sophus::SO(3)可以直接从旋转矩阵构造
Sophus::SO3 SO3_v(0, 0, M_PI/2); // 亦可从旋转向量构造
Eigen::Quaterniond q(R);// 或者四元数
Sophus::SO3 SO3_q( q );

/********************** SE3 **************************/
Eigen::Vector3d t(1,0,0);           // 沿X轴平移1
Sophus::SE3 SE3_Rt(R, t);           // 从R,t构造SE(3)
Sophus::SE3 SE3_qt(q,t);            // 从q,t构造SE(3)

(2)求出对应的李代数

/********************** SO3 **************************/
// 使用对数映射获得它的李代数
Eigen::Vector3d so3 = SO3_R.log();

cout<<Sophus::SO3::hat(so3)<<endl;// hat 为向量到反对称矩阵
cout<<Sophus::SO3::vee(Sophus::SO3::hat(so3));// 相对的，vee为反对称到向量

/********************** SE3 **************************/
// 李代数se(3) 是一个六维向量，方便起见先typedef一下
typedef Eigen::Matrix<double,6,1> Vector6d;
Vector6d se3 = SE3_Rt.log();

// 在Sophus中，se(3)的平移在前，旋转在后.
cout<<Sophus::SE3::hat(se3)<<endl;
cout<<Sophus::SE3::vee( Sophus::SE3::hat(se3) )<<endl;

(3)增量扰动模型的更新

/********************** SO3 **************************/
Eigen::Vector3d update_so3(1e-4, 0, 0); //假设更新量为这么多
Sophus::SO3 SO3_updated = Sophus::SO3::exp(update_so3)*SO3_R;

/********************** SE3 **************************/
Vector6d update_se3; //更新量
update_se3.setZero();
update_se3(0,0) = 1e-4d;
Sophus::SE3 SE3_updated = Sophus::SE3::exp(update_se3)*SE3_Rt;

3 李群与李代数习题

课本后面有一些练习的证明题，使用matlab验证了一下，比较偷懒，所以不能叫证明，只能说是验证。。。

3.1 $验证 S O (3), S E (3), S i m (3) 关于乘法成群$

$设R_1,R_2属于SO(3),有余SO(3)群是具有连续光滑性质的群，令R_3=R_2R_1$ ，对任意三维向量 $V_1=[x,y,z]^T$ ,连续做如下式两次旋转，得到向量 $V_2$
$V_2=R_2R_1V_1=R_3V_1$
当然 $V_2$ 也可以由 $V_1$ 经一次旋转得到，其中 $R_4$ 是属于 $S O (3)$ 群的
$V_2=R_4V_1$
注意到有下式成立
$R_4=R_3$
所以 $R_3$ 是属于 $S O (3)$ 群的，也就是 $R_2R_1$ 是属于 $S O (3)$ 群的,从而验证 $S O (3)$ 关于乘法成群。

$S E (3), S i m (3) 关于乘法成群$ 验证同理。

3.2 验证 $R^3,R,×)构成李代数$

也就是验证三维向量集合见关于叉乘运算封闭。
设三维向量 $V_1, V_2, V_3\in R^3 , [V_1, V_2]=V_1×V_2$

封闭性
$[V_1, V_2]+b[V_2, V_3]=V_1×V_2\in R^3$
符合条件
双线性
$aV_1+bV_2, V_3]=(aV_1+bV_2)×V_3=aV_1×V_3+bV_2×V_3=a[V_1, V_2]+b[V_2, V_3]$
符合条件
自反性
$V_1, V_1]=V_1×V_1=0$
符合条件
雅可比等价
也就是证明
$V_1, [V_2, V_3]]+[V_2, [V_3, V_1]]+[V_3, [V_1, V_2]]=0$
其中，
$V_1, [V_2, V_3]]=V_1×(V_2×V_3)$
$V_2, [V_3, V_1]]=V_2×(V_3×V_1)$
$V_3, [V_1, V_2]]=V_3×(V_1×V_2)$
将三个向量用 $i, j, k$ 三个分量展开，然后带入相加化简得到0。
使用Matlab证明如下，

syms i1 j1 k1 i2 j2 k2 i3 j3 k3 v1 v2 v3 v4;

v1=[i1,j1,k1];
v2=[i2,j2,k2];
v3=[i3,j3,k3];
v4 = cross(v1,cross(v2,v3))+cross(v2,cross(v3,v1))+cross(v3,cross(v1,v2));
simplify(v4)

% 运行结果为 [ 0, 0, 0]

3.3 验证下面的李代数满足李代数要求的性质

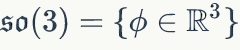
在这里插入图片描述
使用Matlab编写符号函数来证明。
由向量生成反对称阵函数如下

function [ y ] = hat( x )
x = sym(x);
y = sym(zeros(3,3));
y(1,2)=-x(3);
y(1,3)=x(2);
y(2,1)=x(3);
y(2,3)=-x(1);
y(3,1)=-x(2);
y(3,2)=x(1);
end

由反对称阵生成向量的函数

function [ y ] = vee( r )
r = sym(r);
y = sym(zeros(1,3));
y(1) = r(3,2);
y(2) = r(1,3);
y(3) = r(2,1);
end

进行 $\mathfrak{so}(3)$ 的李括号运算函数

function [ y ] = SO3_lie_bracket(x1,x2)
x1 = sym(x1);
x2 = sym(x2);

X1 = hat(x1);
X2 = hat(x2);

y = vee(X1*X2-X2*X1);
end

证明过程如下
(1) 定义三个向量如下

clear;clc;
syms i1 j1 k1 i2 j2 k2 i3 j3 k3;

x=[i1,j1,k1];
y=[i2,j2,k2];
z=[i3,j3,k3];

(2)证明双线性

%  双线性
syms a b;
left = SO3_lie_bracket(a*x+b*y, z);
right = a*SO3_lie_bracket(x,z)+b*SO3_lie_bracket(y,z);
simplify(left-right)% 结果为[ 0, 0, 0]，证明双线性成立

(3)证明自反性

% 自反性
simplify(SO3_lie_bracket(x,x))% 结果为[ 0, 0, 0]，证明自反性成立

(4)证明雅克比等价

% 雅克比等价
part1 = SO3_lie_bracket(x,SO3_lie_bracket(y,z));
part2 = SO3_lie_bracket(y,SO3_lie_bracket(z,x));
part3 = SO3_lie_bracket(z,SO3_lie_bracket(x,y));
simplify(part1+part2+part3) % 结果为[ 0, 0, 0]，证明雅克比等价成立

3.4 证明 $a^{\wedge}a^{\wedge}=aa^T-I和a^{\wedge}a^{\wedge}a^{\wedge}=-a^{\wedge}$ 成立，其中 $a$ 是长度为1的三维方向向量

(1) 证明 $a^{\wedge}a^{\wedge}=aa^T-I$ 成立
只需证明 $a^{\wedge}a^{\wedge}-aa^T-I=0_{3×3}$
利用Matlab化简

syms i1 j1 k1
x=[i1,j1,k1];

simplify(hat(x)*hat(x)-x'*x+sym(eye(3)))

化简结果是

[ 1 - j1^2 - k1^2 - abs(i1)^2, -(j1*(abs(i1)^2 - i1^2))/i1, -(k1*(abs(i1)^2 - i1^2))/i1]
[ -(i1*(abs(j1)^2 - j1^2))/j1, 1 - i1^2 - k1^2 - abs(j1)^2, -(k1*(abs(j1)^2 - j1^2))/j1]
[ -(i1*(abs(k1)^2 - k1^2))/k1, -(j1*(abs(k1)^2 - k1^2))/k1, 1 - i1^2 - j1^2 - abs(k1)^2]

由于 $a$ 是长度为1的三维方向向量, 则有 $i1^2+j1^2+k1^2=1$
最终为 $0_{3×3}$ ，得证。

(2)证明 $a^{\wedge}a^{\wedge}a^{\wedge}=-a^{\wedge}$
只需证明 $a^{\wedge}a^{\wedge}a^{\wedge}+a^{\wedge}=0_{3×3}$ 成立
利用Matlab化简

syms i1 j1 k1
x=[i1,j1,k1];

simplify(hat(x)*hat(x)*hat(x)+hat(x))

化简结果是

[                            0,  k1*(i1^2 + j1^2 + k1^2 - 1), -j1*(i1^2 + j1^2 + k1^2 - 1)]
[ -k1*(i1^2 + j1^2 + k1^2 - 1),                            0,  i1*(i1^2 + j1^2 + k1^2 - 1)]
[  j1*(i1^2 + j1^2 + k1^2 - 1), -i1*(i1^2 + j1^2 + k1^2 - 1),                            0]

由于 $a$ 是长度为1的三维方向向量, 则有 $i1^2+j1^2+k1^2=1$
最终为 $0_{3×3}$ ，得证。