一,无穷级数的定义
- 通项:
- 部分和:
- 余项:
- 离散的和:
- 连续的和(反常积分):
二,级数的收敛和发散
- 收敛:
,s为任意数
- 余项
,其中截断误差为
- 发散:
,或者不存在
三,等比级数,(
)的敛散性
- 展开:
- 通项:
,公比:
- 假设
:
- 等比数列求和公式
- 当
时,
,
,级数收敛
- 当
时,
,
,级数发散
- 假设
:
,级数发散
- 假设
:
- 展开:
- 当n为奇数时,
,
- 当n为偶数时,
,
不存在,级数发散
- 总结:只有当
时,等比级数收敛,
,a是首项
四,收缩级数的敛散性
- 展开:
- 部分和:
- 求极限:
- 级数收敛
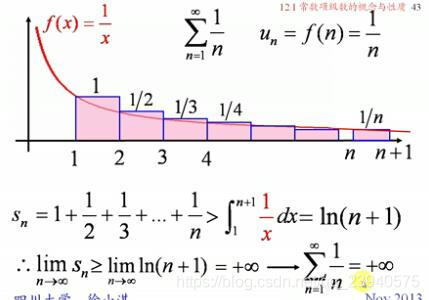
五,调和级数的敛散性
- 展开:
- 部分和没有表达式
- 证明,如图:
























 1117
1117

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








