能量原理和变分法笔记1：变分法简介

上个学期在学校学了多体系统动力学的课，其中老师讲了变分原理，觉得很有启发，决定再学学相关的知识，在B站找到了一个这样的视频能量原理与变分法，做点笔记，加深一下理解。

第0章

序言-微元、功和能(P2)

上述三种方式是等价的，其中

第一种表示形式$2x=0$是微元，对应于局部，没一点都有这样的形式；
第二种表示形式$2xdx=0$类似于求功，微分是一个虚功，积分就是整个区域的功，所以是全局的；
第三种表示形式$d{x}^2=0$等价求函数$x^2$的极值，可以看做是一种能量的角度，也是全局的形式。

这些形式有什么实际意义呢？本质上他们是等价的，但是是从不同的角度对一个问题进行描述。

微元从微观出发，把系统里的各个对象进行拆分，可以对应于静力学的平衡微分方程，也可以对应动力学的牛顿欧拉方程/拉格朗日方程。

功也是一个全局的概念，我们从物理里知道功是一个过程量，这可以对应于静力学和动力学的虚位移原理。

能量也是一个全局的概念，可以对应于静力学的最小势能原理和动力学的Hamilton原理。

类似的，下面的例子我们也很容易理解了：

对于微元和功的形式（第一种和第二种形式），我们总能找到，但是对于第三种形式呢，能量的形式我们是不是一定能找到呢？

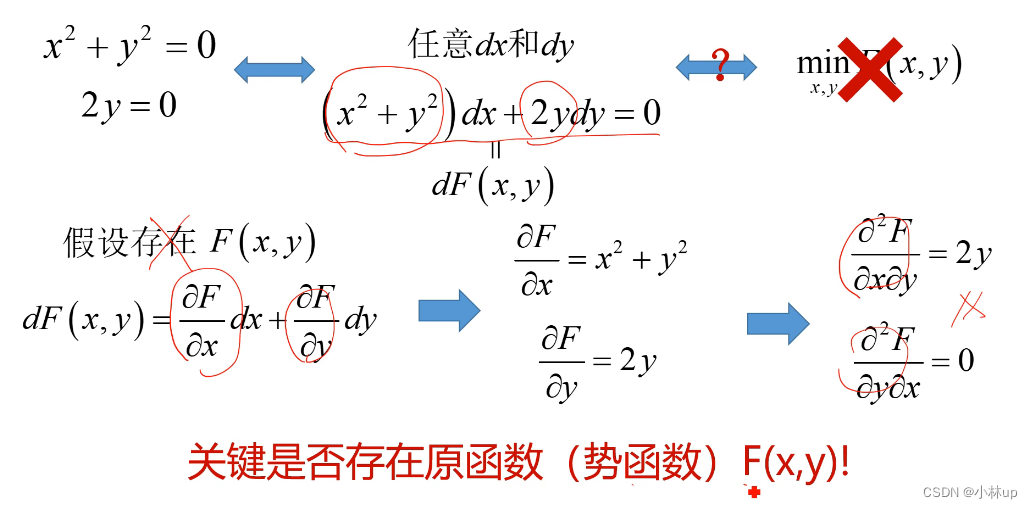
上面的例子很好地解释了这个问题，不一定能找到能量对应的原函数！

对于能的描述对应于求解一个优化问题，无约束优化问题很好求解，我们来看有约束优化问题，一般有以下两种方法：

第一种是代入消元法的思想，类似于力学上的最小势能原理和最小余能原理，但是缺点在于约束条件必须满足。

第二种是使用拉格朗日乘子的方法，在高数课上有讲过，这时候可以转换为一个无约束的优化问题，约束条件不用满足，这称为识别因子的拉格朗日乘子法。

第1章

1.1-引言：微元、功和能举例(P3-P4)

• 举一个实际的例子，一个外力加在一个弹簧牵引的小车上。然后分别使用了微元、功和能量的原理，进行一个位移的求解。
  

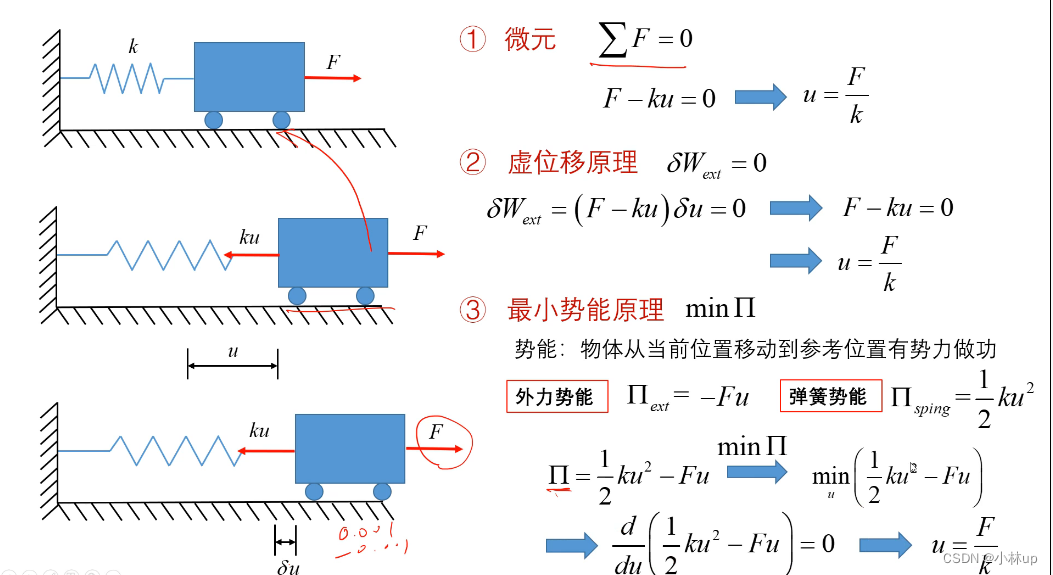
• 再举一个实际的例子，比如说有这样一根杆。它的一端固定在墙上，另一端用外力拉。那么这时候可以用微元、用功和用能的方法进行一个求解。在用能的方法中，需要使用泛函求极值的方法，这就是我们要讲的变分法。
  
  
  
  

1.2-几个典型的例子：变分法举例(P5)

• 两点之间直线最短
  
• 最速降线问题

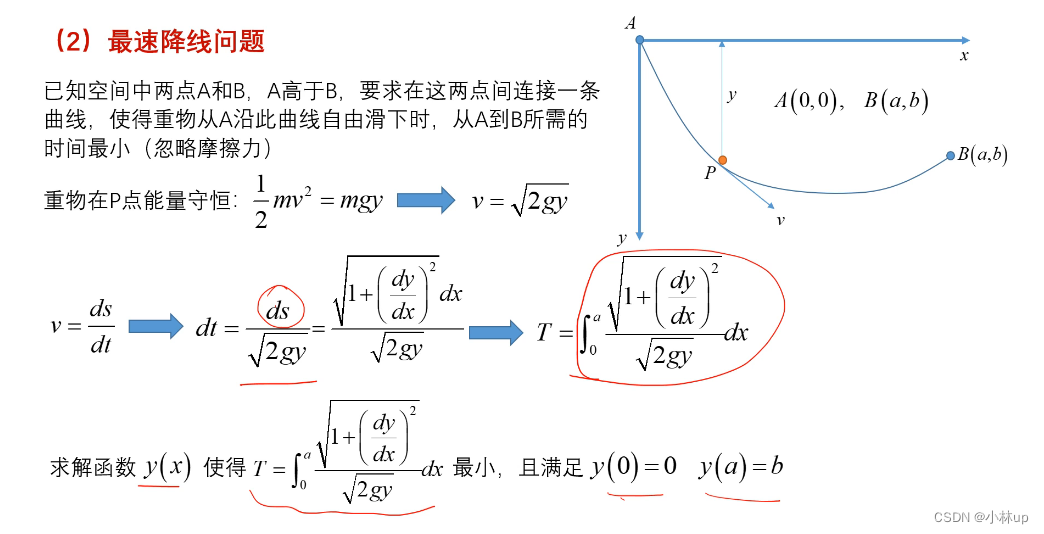
1.3-泛函变分问题及其解法(P6-P9)

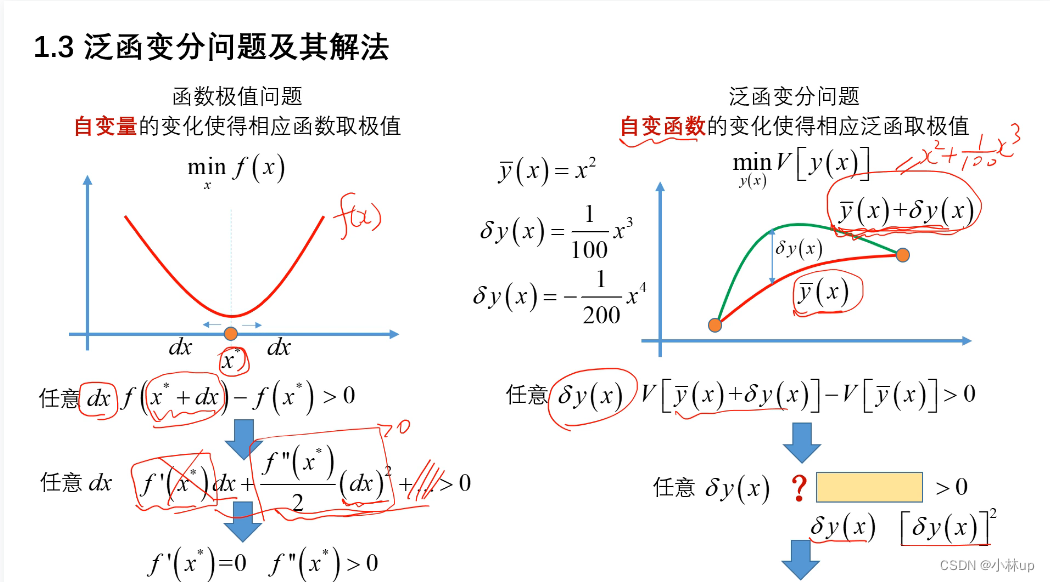
具体的求解方法如下，分别给出了函数求极值的方法和泛函求极值的例子。

再拿第1章第2节的两点之间直线最短来进行举例。

类似于函数求极值的方法，我们可以同样给出泛函变分的一阶小量。

在函数求极值的过程当中，我们知道，例如说$2xdx+2ydy=0$, $dx$和 $dy$任意的话，我们可以直接让$2x=0$,$2y=0$。但是在泛函变分一阶小量中，我们是不是也可以这样做呢？就是让$\frac{\partial F}{\partial y}=0$, $\frac{\partial F}{\partial y^{\prime }}=0$。是不可以的。因为$y$和$y‘$，两者并不独立。

微分和变分的可交换性推导。

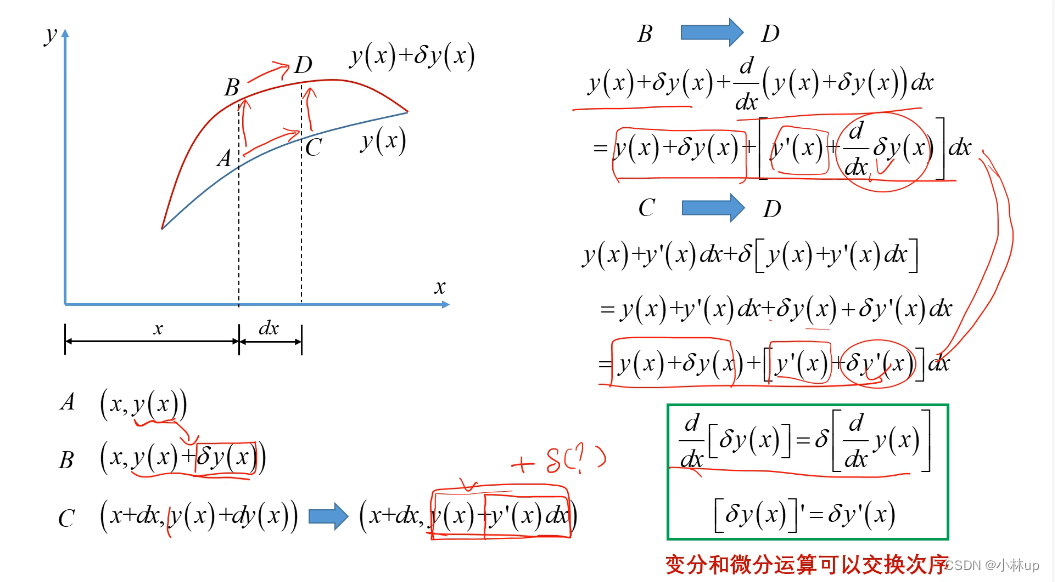
利用分步积分法于是就可以得到下面的推导。
结论是:
$$\delta V[y(x)]={\int }_a^b\left[\frac{\partial F}{\partial y}-\frac{d}{dx}\left(\frac{\partial F}{\partial y^{\prime }}\right)\right]\delta ydx=0$$

于是推导出了欧拉方程。
$$\frac{\partial F}{\partial y}-\frac{d}{dx}\left(\frac{\partial F}{\partial y^{\prime }}\right)=0$$

求解变分问题可以有下面的两种思路：

1.精确解（间接解法）

求解欧拉方程：这是一个二阶微分方程。例如对上述的两点之间直线最短的问题。如果求解精确点的话，那么就要穷举两点之间所有的曲线，这是不可能的，因为它有多种的形式，可能是一次，二次三次甚至高次。甚至非多项式的形式。使用穷举法是有缺陷的。所以这个时候可以使用近似解。比如只是使用二次曲线去进行逼近。找出最可能的二次曲线作为他的近似解。

2.近似解（直接解法）

求解优化问题：使用泛函求极值的方法进行求解。

求解两点之间直线最短。
1.精确解（间接解法）

2.近似解（直接解法）

最速降线问题。
1.精确解（间接解法）

2.近似解（直接解法）

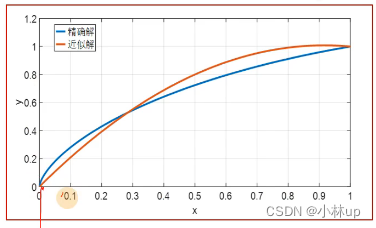
为了提高近似解的求解精度，可以把函数增加三次项，四次项。来扩大函数的范围。

1.4-自然边界条件(P10-P11)

我们上面所讲的条件是满足两端点的一个边界条件。如果只要求一端满足边界条件，比如$y(a)=\alpha$。而对另一端没有边界条件的限制，那么我们可以得到什么样的结论呢？

上面一页的第一行根据分步积分法推导的等式。有个减号写成了加号，正确的写法应该是：

$$\begin{array}{rl}& \delta V\left[y(x)\right]={\int }_a^b\left\{\frac{\partial F}{\partial t}\delta y+\frac{\partial F}{\partial y^{\prime }}\delta y^{\prime }\right\}dx=\frac{\partial F}{\partial y^{\prime }}\delta y{|}_a^b+{\int }_a^b\left[\frac{\partial F}{\partial y}\delta y-\frac{d}{dx}\left(\frac{\partial F}{\partial y^{\prime }}\right)\delta y\right]dx=0\\ \to & \delta V\left[y(x)\right]={\int }_a^b\left[\frac{\partial F}{\partial y}-\frac{d}{dx}\left(\frac{\partial F}{\partial y^{\prime }}\right)\right]\delta ydx+\frac{\partial F}{\partial y^{\prime }}{|}_{x=b}\delta y(b)=0\end{array}$$

由于$\delta y$或者$\delta y(b)$任意,于是我们可以得到两个重要的等式。

$$\begin{gathered} \frac{\partial F}{\partial y}-\frac{d}{dx}\left(\frac{\partial F}{\partial y^{\prime }}\right)=0 \\ \frac{\partial F}{\partial y^{\prime }}{|}_{x=b}=0 \end{gathered}$$

其中第二个式子就是自然边界，对于一个优化问题，它自然就会给出一个自然边界，不需要事先给定。而$y(a)=\alpha$是本质边界。利用这两个边界条件就可以求解欧拉方程所对应的二次微分方程，对应的是上述的间接解法（精确解）。

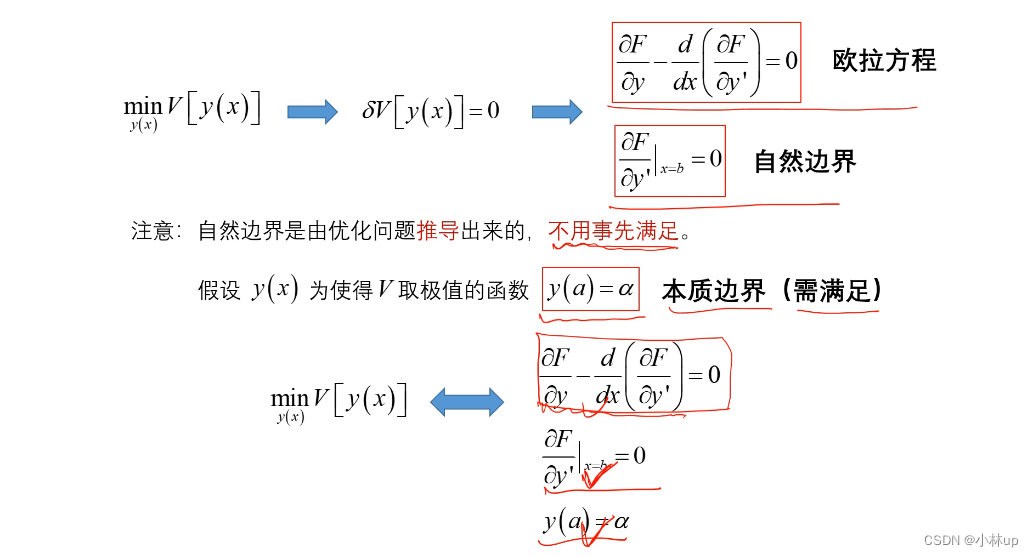
如果按照直接解法由泛函求极值的方法来求解可能的$y(x)$，那么我们需要注意的是，自然边界是根据这个优化问题直接给出来的，我们就不需要去考虑函数如何去满足自然边界（自然边界是被自动满足的）。我们只需要考虑满足于本质边界的一系列函数。来求解这样的一个优化问题。

举个例子，点到直线垂线距离最短。

下面一张图片是求解精确解，我们可以看到求解精确解的时候。自然边界和本质边界都需要用到。

下面来看用直接解法来求解近似解，近似解是直接利用泛函求极值来求解。这里给出了两种近似解的形式，我们在这两种形式当中寻找最可能的那个解。我们可以看到：

• 近似解为$y=ax$的形式时，得到了$y(x)=0$，这个形式其实包含了精确解，所以我们得到一个精确解。也就是过点做直线的垂线。我们可以验证。这个形式的近似解既满足本次边界也满足自然边界。。
• 近似解为$y=a{x}^2-x$的形式时，得到了$y=\frac{3}{4}{x}^2-x$,这个形势没有包含精确解。我们可以进一步验证，这种形式的解只满足本质边界而不满足自然边界。
  
  总结：

对于下式我们同样可以推导自然边界：
$$\delta V\left[y(x)\right]={\int }_a^{b}F(x,y,y^{\prime })dx+Py(a)+Qy(b)$$
我们有自然边界（推导看下面的图）
$$\begin{gathered} \frac{\partial F}{\partial y^{\prime }}{|}_{x=a}=P \\ \frac{\partial F}{\partial y^{\prime }}{|}_{x=b}=Q \end{gathered}$$

1.5-高阶导数的变分问题(P12)

对于高阶导数求变分问题它的本质边界和自然边界如下：

下面这个例题题目有误，原题漏了平方，增加了以后才和原答案是一样的。正确应该为

$$V\left[w(x)\right]={\int }_0^l\left[\frac{D}{2}{\left(\frac{d^{2}w}{d{x}^2}\right)}^2+\frac{N}{2}\left(\frac{dw}{dx}\right)+\frac{k}{2}{w}^2-qw\right]dx,\underset{w(x)}{\min }V[w(x)]$$

1.6-多个自变函数的变分问题(P12)

对于多个自变函数的变分问题，一般是用在动力学上。我们同样可以给出他的欧拉方程、本质边界和自然边界。

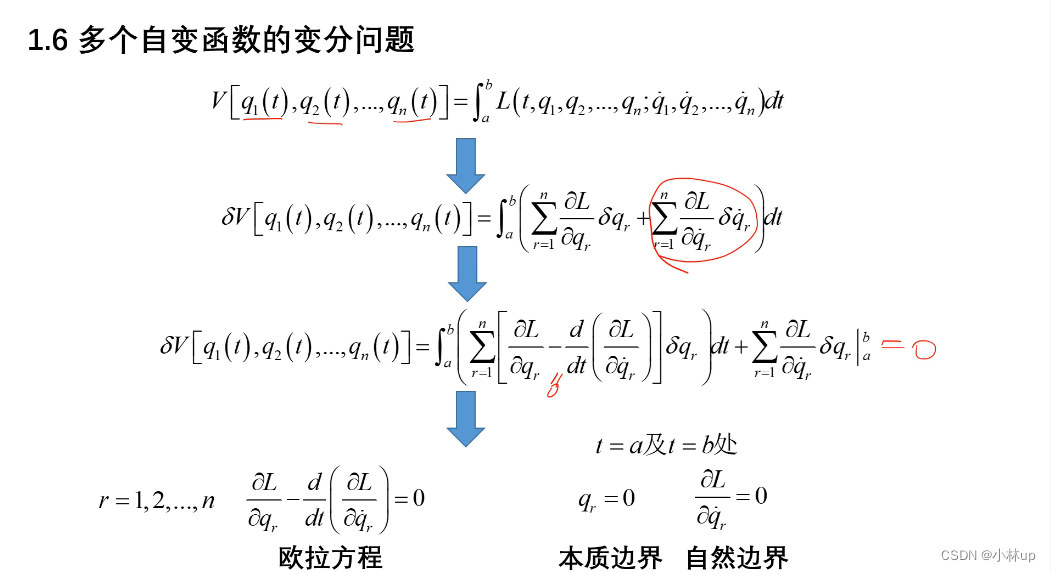
对于条件极值的变分法，我们同样可以给出：

1.7-条件极值的问题的变分法(P13)

1*-思考题