1 自动控制系统的基本原理
1.1 引入以及定义
诸如:神舟10号发射升空、战斧式巡航导弹、装配机器人、自动泊车系统等其中都应用了自动控制的相关理论和技术。
-
什么是控制?
控制 - 使某个(某些)量按一定的规律变化某个(某些)量=》我们取名为 “被控制量”
具体示例:
-
神舟九号与天宫一号的交汇对接
被控制量是神舟九号与天宫一号的相对距离。 -
导弹的控制问题
导弹与目标的相对距离ρ为被控制量,最终必须趋向于0。 -
高射炮的控制问题
高射炮的俯仰角 α 和方位角 β是两个被控制量。

-
雷达天线随动系统
-
钢板厚度的控制问题
通过控制轧制力,使钢板厚度均匀。

-
退火炉的温度控制
为了防止在退火过程中工件产生内应力,退火炉内的温度应该按照图示曲线的规律变化。

在这个例子中,炉内温度就是被控制量。当外界环境温度的改变对炉内温度产生干扰时,炉内温度仍然应该按照预定的规律变化,而不受干扰的影响。这就是自动控制的目的。
对上面的例子进行总结和归纳得出如下定义:
- 自动: 就是不需要人的介入;
- 自动控制: 在脱离人的直接干预下,利用控制装置,使被控对象按照预定的规律运行;
- 自动控制系统: 将被控的对象和实现控制功能的控制装置组合起来称为自动控制系统。
1.2 自动控制的优点
- 可以快速准确地进行控制,比人工控制效果更好;
- 使人们从繁重的、大量的重复性劳动中解放出来;
- 在恶劣的环境或人们无法到达的环境中实现自动控制;
- 可以长时间不疲劳的工作,以提高工作效率
实例:

1.3 术语
(1)被控对象 (也称被控过程、被控系统)
- 它可能是一个设备,多数由一些机器零件有机地组合在一起,其作用是完成一种特定的操作。
(2)被控参数(也称为系统输出)
- 体现系统控制目的的物理量。(距离、方位角度等)
(3)控制参数
- 由控制器改变的量,对被控参数有较好的调节能力。(阀门开度、电枢电压等)
(4)系统输入
- 作用于被控对象或系统输入端,并可使系统具有预定功能或预定输出的物理量。(给定温度,电位器滑杆位置)
(5)扰动
- 一种对系统的输出量产生影响的信号。(水箱出水、负载等)
(6)开环控制:输出量对输入量(控制作用)没有影响的系统。

缺点:没有抵抗扰动的能力。
(7)※ 闭环控制:将输出量与参考输入量进行比较,并且将它们的偏差作为控制手段,以保持两者之间预定关系的系统,也称为反馈控制系统

将输出量反送到输入端,与输入端形成偏差称之为反馈
控制系统中主要采用负反馈 。
负反馈:反馈的加入,使偏差越来越小。
正反馈:反馈的加入,使偏差越来越大。(振荡发生器)
最大的特点:
- 消除偏差;
- 使系统对参数不敏感。
1.4 控制系统的组成

※ 本节最重要的概念:负反馈 闭环控制系统
2 自动控制系统的分类
对研究对象的正确分类是分析对象的重要环节。分类原则: 不遗漏,不重叠
- 按输入信号的变化规律分
定值控制:参考输入为一个恒定的值。如速度控制、液位控制等
程序控制:参考输入为一个已知的时间函数。如自动驾驶、热处理过程等。
随动控制:参考输入为一个随机变化的函数。如雷达天线跟踪系统等。
- 按系统中传递信号的特点分
连续系统:系统中传递的信号都是时间轴上连续的信号。描述对象的数学模型是微分方程。

离散系统:系统中某一处或几处信号为脉冲序列或时间轴上不连续的信号。描述此类系统的数学模型为差分方程。如计算机控制系统。

-
按系统特点分
线性系统: 组成系统的所有元件或子系统都是线性的。- 线性定常连续系统

非线性系统:系统中至少有一个元件或子系统是非线性的。

- 线性定常连续系统
-
按系统输入输出数量分
单输入单输出(经典控制理论)如:电动机速度控制系统
多输入多输出(现代控制理论) -
按系统功能分
温度控制、
速度控制、
位置控制
… -
按组成元件的特点分
机械系统、
电气系统、
液压系统、
生物系统、
经济系统
…
3 自动控制系统的基本要求
- 建立控制系统的目的
- 保证系统输出具有控制输入指定的数值
- 保证系统输出尽量不受扰动的影响
- 对系统的具体要求
(1)系统稳定性
(2)系统动态快速性
(3)系统的稳态准确性
为了使闭环控制系统能够正常工作,能够满足设计者和使用者的要求,必须对控制系统提出一些要求。
(1)稳定性
稳定性是保证控制系统能够正常工作的先决条件

(2)快速性
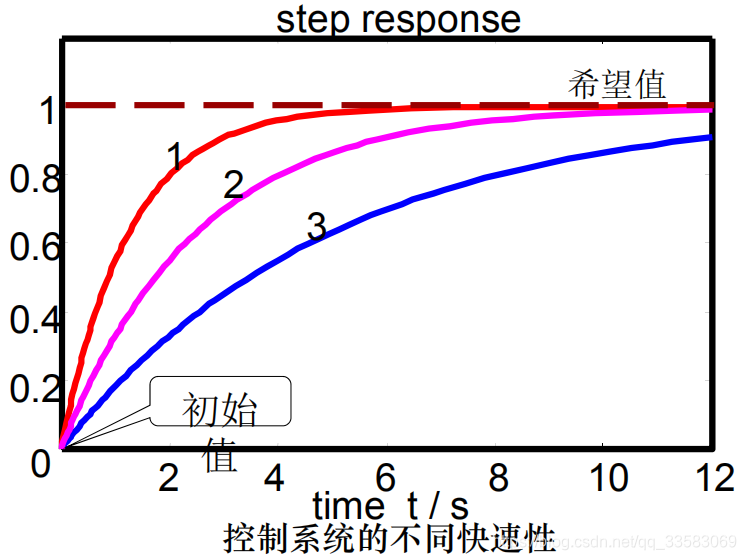
要求被控制量由初始值变为另一希望值,某些控制系统可以快速响应,如下图中的曲线1;而某些控制系统则响应十分缓慢,如下图中的曲线3。显然,能够快速响应的系统性能更好。一般来说,我们总是要求控制系统具有很好的快速性。
(3)平稳性
当被控制量由初始值变为另一个希望值时,某些控制系统会出现超调现象。即被控制量会超过希望值,并经过若干次摆动以后才达到希望值。如下图中的曲线1所示。如果控制系统设计得好,被控制量会平稳地达到希望值,不出现大幅的摆动,如下图中的曲线3所示。

(4)准确性
如果要求被控制量由初始值变为另一个希望值时,在变化过程结束后,被控制量能够达到希望值,说明该系统具有很好的准确性,如下图的曲线1所示;如果被控制量在变化过程结束后不能达到希望值,存在很大的误差,说明该系统的准确性很差,如下图的曲线2所示

以上四项对控制系统的要求可以归纳为“稳、快、 平、准”四个字。其中,快速性和平稳性反映控制系统的动态品质;准确性反映反映控制系统的稳态精度;而稳定性则是控制系统能够正常工作的先决条件。
自动控制原理课程的任务:
研究一种方法(或理论)来指导构筑一个控制系统达到系统目标。
具体:
设计控制装置以达到系统的目的
细化为:
1、了解各种元器件或子系统的运动规律、动力学方程(建立数学模型)
2、了解某种控制器对系统输出的影响(系统分析)
3、设计控制器(系统设计或系统综合)
4 自动控制的发展历史
-
前期控制(1400 BC–1900) 工业机器
- 中国,埃及和巴比伦出现自动计时漏壶 (1400 BC–1100BC);
- 希腊Philon发明了采用浮球调节器来保持燃油液面高度的油灯(BC250)
- 中国张衡发明水运浑象,研制出自动测量地震的候风地动仪(132)
- 中国马钧研制出用齿轮传动的自动指示方向的向的指南车 (235年);
- 英国 J. Watt用离心式调速器控制蒸汽机的速度 (1788年)。
-
经典控制(1935 --1950) 空间技术
- 美国 N. Minorsky 研制出用于船舶驾驶的伺服结构,提出PID控制方法 (1922);
- 美国 E. Sperry以及C. Mason 研制出火炮控制器(1925),气压反馈控制器 (1929);
经典控制理论阶段(以传递函数作为系统数学模型)
1868年麦克斯韦尔(J.C.Maxwell)基于微分方程描述从理论上给出了它的稳定性条件。
1877年劳斯(E.J.Routh),1895年霍尔维茨(A. Hurwitz)分别独立给出了高阶线性系统的稳定性判据;
1892年,李雅普诺夫(A.M.Lyapunov)给出了非线性系统的稳定性判据。
在同一时期,维什哥热斯基(I.A.Vyshnegreskii)也用一种正规的数学理论描述了这种理论。
1922年,米罗斯基(N.Minorsky)给出了位置控制系统的分析,并对PID三作用控制给出了控制规律公式。
1942年,齐格勒(J.G.Zigler)和尼科尔斯(N.B.Nichols) 又给出了PID控制器的最优参数整定法。
上述方法基本上是时域方法。
1932年柰奎斯特(Nyquist)提出了负反馈系统的频率域稳定性判据。
1940年,波德(Bode)进一步研究通信系统频域方法,提出了频域响应的对数坐标图描述方法。频域分析法主要用于描述反馈放大器的带宽和其他频域指标。
1943年,霍尔(A.C.Hall)利用传递函数(复数域模型)和方框图,把通信工程的频域响应方法和机械工程的时域方法统一起来,人们称此方法为复域方法。
1948年伊文斯(W.Evans)又进一步提出了属于经典方法的根轨迹设计法,它给出了系统参数变换与时域性能变化之间的关系。总结:经典控制理论的分析方法为复数域方法,以传递函数作为系统数学模型。
优点:可通过试验方法建立数学模型,物理概念清晰。
缺点:只适应单变量线性定常系统,对系统内部状态缺少了解。 -
现代控制(1950 --Now) 控制理论 (以状态空间表达式为模型)
现代频域方法,自适应控制理论和方法、鲁棒控制方法等
状态空间方法属于时域方法,其核心是最优化技术。它以状态空间描述(实质上是一阶微分或差分方程组)作为数学模型,适应于多变量、非线性、时变系统
大系统控制理论阶段
20世纪70年代,随着控制理论应用范围的扩大,人们开始了对大系统理论的研究。
大系统理论是过程控制与信息处理相结合的综合自动化理论基础,是动态的系统工程理论,具有规模庞大、结构复杂、功能综合、目标多样、因素众多等特点。
它是一个多输入、多输出、多干扰、多变量的系统。
大系统理论目前仍处于发展和开创性阶段。
智能控制阶段
依据人的思维方式和处理问题的技巧,解决那些目前需要人的智能才能解决的复杂的控制问题。
- 被控对象的复杂性体现为:模型的不确定性,高度非线性,分布式的传感器和执行器,动态突变,多时间标度,复杂的信息模式,庞大的数据量,以及严格的特性指标等。
- 环境的复杂性则表现为变化的不确定性和难以辨识。
- 试图用传统的控制理论和方法去解决复杂的对象,复杂的环境和复杂的任务是不可能的。
- 智能控制的方法包括模糊控制,神经元网络控制,专家控制等方法。


























 1569
1569

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










