中正平和的机器人学笔记——2. 机械臂逆运动学（附MATAB代码）

0. 预备知识（别跳过呀）

上一篇我们讲了正运动学，也就是通过齐次变换矩阵，知晓关节角后求得机械臂末端的位姿，并表示在基座标系下。这一篇我们就来讲一讲逆运动学问题——已知工具坐标系{T}相对于固定坐标系{S}的期望位姿，如何计算一系列满足期望要求的关节角？

0.1 求解的难度

这是一个难度更大的问题，因为求解操作臂运动学方程是一个非线性问题。譬如六自由度的机械臂Puma560，回顾最后求得的运动学方程，

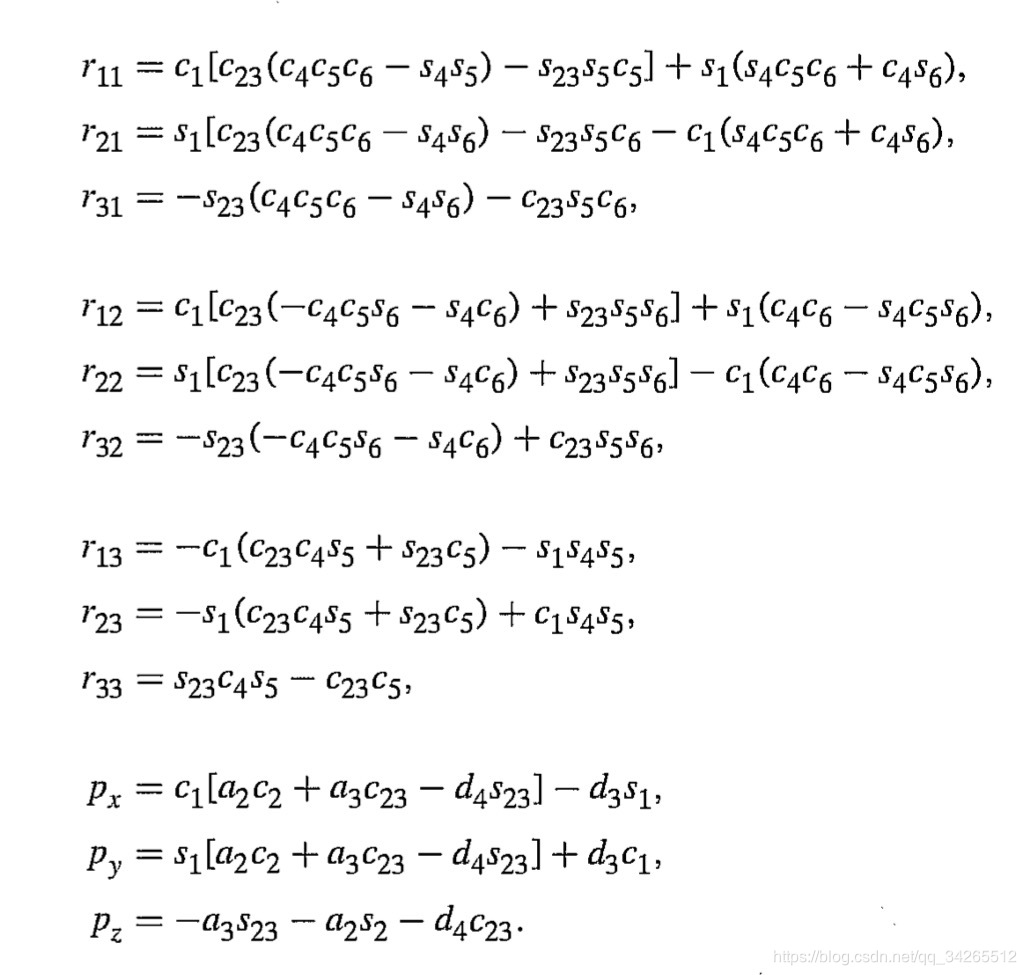
这里我们一共有12个方程，6个未知数。旋转部分3×3的矩阵由于每一列都是单位矢量，两两正交，因此这9个方程只有3个是独立的。再加上第四列前三行位置矢量的三个方程，6个方程对应6个未知数，应当是有解的。但是其中含有sin和cos，是非线性超越方程，求解难度很大，应到考虑到解是否存在，多解以及求解方法的问题。

0.2 解的存在性

这里引入三个概念，
工作空间（workspace）：操作臂末端的执行器所能达到的范围。
灵巧工作空间（dexterous workspace）：机器人末端执行器能从各个方向达到的空间。
可达工作空间（reachable workspace）：机器人至少从一个方向上可以道德的空间。

从上述概念可以分析得到，如果要求解存在，那么期望点一定在工作空间内才行。
我们以两连杆机械臂为例，如果l1 = l2 = r，且关节旋转角能达到360°，那么其可达工作空间为半径为2r的圆，灵巧工作空间为原点；如果l1 ≠ l2，那么可达工作空间为外径l1 + l2，内径为|l1 - l2|的圆环，不存在灵巧工作空间。
一般的，当机械臂自由度小于6时，其不能到达三维空间内一般的目标位姿。

0.3 多解问题

多解问题也很好理解，例如Puma560机械臂，对已确定目标可有8个不同解，但往往由于关节运动范围的限制，这8个解中的某些解不能实现。如下图所示：

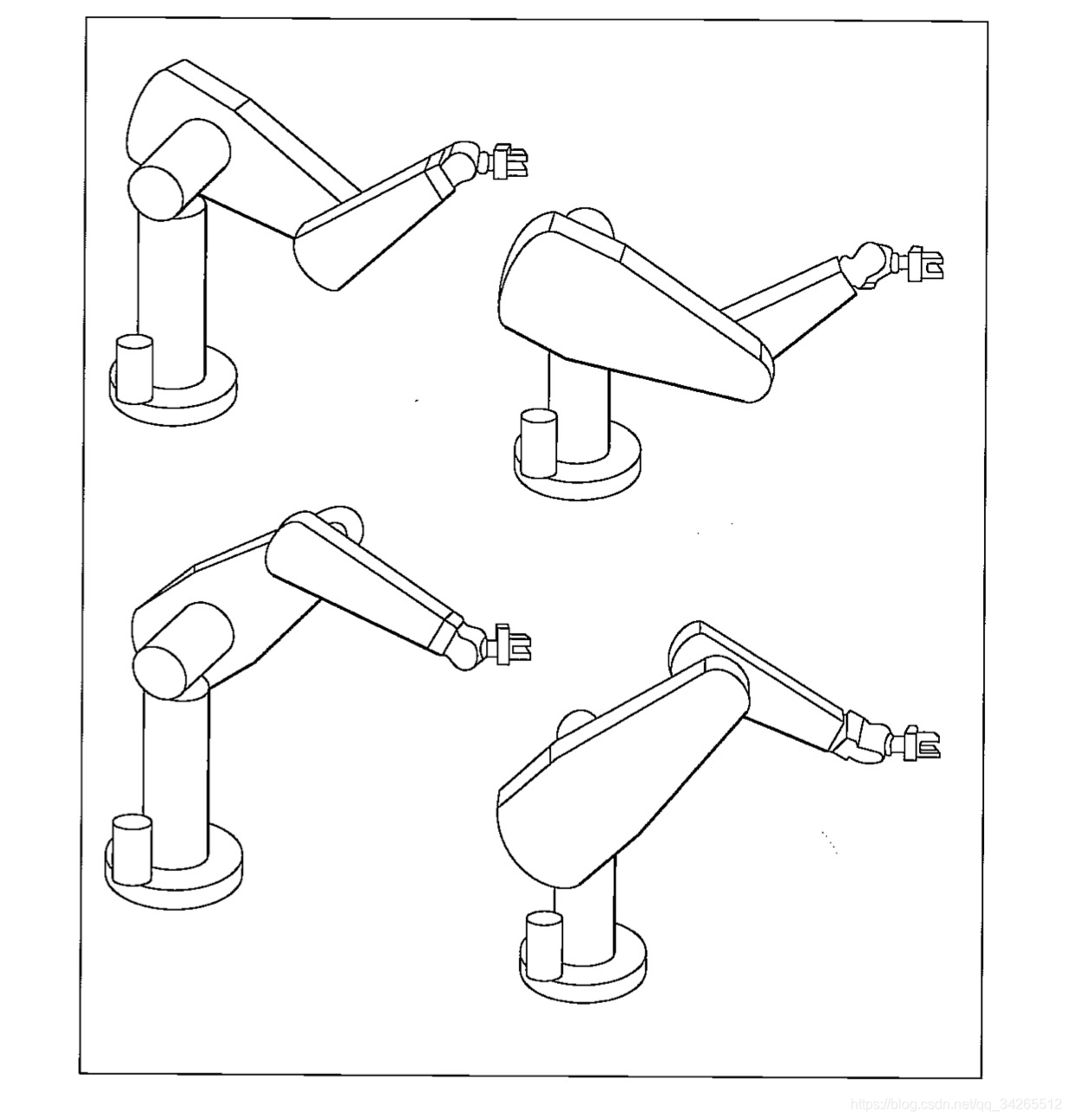
0.4 解法

由于非线性方程组没有通用的求解算法&