VIO综述论文：A review of visual inertial odometry from filtering and optimisation perspectives

参考博客：https://blog.csdn.net/qq_38373843/article/details/91360043

摘要

  视觉惯性里程计(VIO)是一种利用机载摄像机和IMU传感器的测量数据，估计移动平台位置和方向随时间变化的技术。近年来，VIO因其尺寸小和传感器模块价格低廉，受到了大量研究者的关注，并在各种潜在的应用中得到了广泛的应用。然而，考虑到精度、实时性、鲁棒性和运行规模，无论是技术开发或者工程实现都非常具有挑战性。本调查从滤波和优化法两个方面报告了VIO技术的现状，这两种方法在研究领域占主导地位。

1.概述

  定位与建图是机器人导航与控制研究领域的两个基本问题。SLAM技术和SFM（运动恢复结构）技术[1]分别成为机器人和计算机视觉研究领域多年来的主要课题之一。随着人们对将这些技术应用于小型平台(如小型无人机或手持移动设备)的兴趣日益浓厚，定位和建图的研究重点已转向相机和惯性测量单元传感器的使用。由于芯片和微电子机械系统(MEMS)设备的快速发展，这些传感器开始具有高精度、小型化和低成本的特点。它们之间在某种程度上是互补的，通过它们提供的冗余信息可以弥补各自的不足。此外，生物学研究表明，人类和一些动物的导航功能依赖于多种形式的运动传感模式和视觉的结合。[2-4]

  定位与建图问题是机器人中的状态估计问题。对于给定噪声测量的动态系统，随机估计算法如扩展卡尔曼滤波器(EKF)或粒子滤波器(PF)的是主流工具。
  运动模型：一些内部传感器提供了姿态随时间变化的测量，并被表示为一个数据驱动的移动平台运动模型。包括地面移动机器人中的光电编码器和飞行机器人中的IMU。它们以累积误差和偏置测量而闻名。（运动模型使用 IMU和光学编码器测量的数据）
  测量模型：一些外部传感器，如相机或激光测距仪，能够提供角度或距离测量。基于三角测量或三边法，能够估计移动平台的位置或方向。估计的可靠性在很大程度上取决于环境条件，结果对测量噪声敏感。然而，它们可以作为状态估计问题的测量模型。（测量模型使用 相机或激光雷达的测量数据）
  EKF或PF通过融合动态模型中的分布和测量模型中的分布，将估计的分布由前一步传播到当前一步。在大多数情况下，EKF代替PF，因为要估计的状态数量很大。然后，估计高斯分布的均值和协方差。

  视觉运动估计是计算机视觉领域的一个优化问题。通过图像对齐迭代计算相机姿态的变化[6,7]。通常，特征是从一幅图像中提取出来，然后重投影到另一幅从不同视角捕获的图像中。在此基础上，最小化特征与重投影特征之间的误差代价，得到摄像机的姿态变化和环境结构。优化法主要是基于梯度的，如牛顿法或高斯牛顿法。在大多数情况下，利用矩阵的稀疏结构来提高计算效率。只提供估计状态的值，而没有关于估计分布的信息。

  在贝叶斯推理框架下建立滤波法和优化法之间的联系。优化法被看作是一个最大似然(ML)公式，其中迭代地找到测量总概率最高的状态。滤波法被看作是一个最大后验(MAP)公式，其中平台姿态的先验分布由本体感觉传感器的测量值构成，似然分布由外感受传感器的测量值构成。对于非线性动态模型和/或非线性测量模型，迭代EKF等价于基于优化的方法，迭代更新EKF中的每一步。优化法可以通过添加来自内部传感器或其它源测量的正则化项或先验项，将ML问题重新表述为MAP问题。这些是在线或因果算法，其中当前估计依赖于当前和以前的测量。离线或非随机算法是批处理过程，其中当前估计依赖于完整的数据集，或者可以说，它们不仅依赖于当前和以前的测量，而且还依赖于未来的测量。在优化法中，批处理被分解为求解一组线性代数方程。在滤波法中，卡尔曼平滑算法可以通过前向和后向两种方法得到后向高斯分布。

  主流的SLAM技术能够提供平台姿态和环境结构的估计结果。需要闭环检测来约束估计算法产生的累积误差[8-10]。但是，VIO技术中没有显式地执行闭环检测。因此，VIO中的估计错误将会累积，并且无法被约束消除。由于没有闭环检测，小型设备可以实现长时间大规模的定位。因而研究的问题转向了如何利用这些技术来减缓误差的增加。

  本文将介绍VIO技术的最新发展和进展。从滤波和优化的角度，说明了它们的基本模型、算法和最近的结果。调查还将突出两种方法之间的联系，并对VIO技术进行深入的介绍。对状态可观测性和参数可辨识性进行了讨论。总结了对VIO研究领域的展望。

2.基于滤波的方法

  EKF框架一般由预测步骤和更新步骤组成。对于滤波法VIO，惯性传感器能够提供三轴加速度和角速度测量值，作为三维刚体运动的数据驱动动态模型或先验分布，并在预测步骤中进行运动预测。相机能够提供特征与移动平台之间的角度和距离测量，作为测量模型或似然分布，并在更新步骤中更新预测结果。

  假设搭载只有摄像头和IMU的移动平台，在未知环境中移动。相机与IMU之间的空间关系是固定的，可以表示为已知的位置和姿态。基于EKF的VIO算法目标是利用惯性测量和未知环境的视觉观测提供平台的位置和方向信息。接下来，将基于[11]对EKF框架进行全面的描述，包括状态表示、IMU数据驱动的动态和可视化观察。

2.1 IMU数据驱动运动模型

三维刚体任意时刻的IMU状态向量可由一个16×1的向量定义：

${{\overline{q}}_W^I}^T$是描述从世界坐标系到IMU坐标系旋转的单位四元数（旋转） ${\overline{q}}^T=[q_0,q_1,q_2,q_3]$，$p^T和v^T$是相对于世界坐标系的位置（平移）和速度$p^T=[x,y,z]，v^T=[v_x,v_y,v_z]$，$b_g^T和b_a^T$是一个3×1的向量 $b_g^T=[b_{gx},b_{gy},b_{gz}]，b_a^T=[b_{ax},b_{ay},b_{az}]$，分别描述陀螺仪和加速度计的bias，图1所示为两个坐标系之间的空间关系：

在这里，提出了一个只包含一个相机姿态的系统状态，它可以表示为一个$24\times 1$维向量。

其中状态关于时间t的导数为：

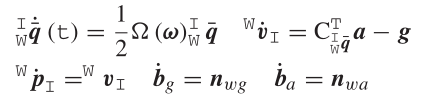
假设惯性测量包含零均值高斯模型的噪声，用$n_g和n_a$表示，实际角速度ω和实际加速度a与陀螺仪和加速度计测量有关，$w_m与a_m$为测量的角速度与加速度，其形式如下：

将上式带入可得：

最后更新状态的过程如下：

$x_k$表示k时刻的状态，$z_k$表示k时刻相机的观测值，$n_{p,k}$表示在 p 点 k 时刻的测量高斯噪声，遵循$n_p\sim N(0,Q)$，$f$表示运动模型（运动方程）。

2.2 状态误差表示及更新

利用估计的状态值与真实状态值的误差更新当前状态，主要使用到高斯分布的均值和IMU、相机的协方差矩阵，其估计状态值$\hat{x}$,实际测量状态值$x$：

其最小旋转误差：

误差状态向量，是一个$22\times 1$维的向量：

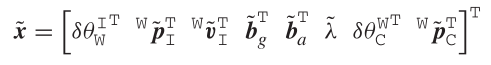
连续时间误差状态的微分方程是：

通过对误差状态微分方程进行叠加，可以得到线性化的连续时间误差状态方程：

基于EKF的VIO框架的均值和协方差传播过程总结如下：

1：当IMU数据ω和$a_m$在一定采样频率下可用于滤波器时，状态向量通过方程（1）的数值积分传播；

2： 分别按公式（4）和（5）计算$F_d和Q_d$;

3：传播状态协方差矩阵由（3）计算得出；

其中EKF滤波器的协方差矩阵定义为：

2.3 视觉观测模型与更新

  由于IMU数据中的偏差和噪声，随着时间的推移，预测步骤的预测结果越来越差。来自视觉传感器的测量将能够提供关键信息来限制增加的误差。在EKF框架下，从图像中提取的关键信息应转化为测量方程。松耦合方法：使用图像对齐直接获得位置和方向变化，再通过EKF框架将两个估计结果融合在一起。紧耦合方法：使用从图像中提取的关键信息。关键信息可以是通过特征检测器从图像中提取的特征，具有深度信息的直接光强度（点云），或者半直接光强度和深度信息，之后将关键信息建模为观测方程，从而提供关键信息和状态变量之间的解析关系。一般来说，一个非线性代数方程可以看作是观测方程：

其中$x_k$表示k时刻的状态，函数 $h$表示观测方程，$z_k$表示在状态$x_k$是观测到的数据，$n_{m,k}$表示k时刻视觉测量的高斯噪声；

线性化后，测量误差以线性形式表示：

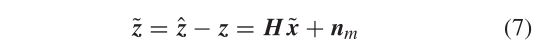
其中$H$为雅可比矩阵，$n_m$噪声项为高斯分布，与状态误差无关。$\hat{z}$ 和 $z$ 分别表示预测和实际测量值。

  利用特征作为视觉信息，最直接的方法是利用针孔模型建立相机坐标系 $C$ 的测量方程。提取图像中的 u$=[u,v]$点来表示关键信息。首先，将相机帧中的u点与世界帧$W$中的$p^w$点之间的空间关系建立如下方程：

其$P_u^w$表示像素在世界坐标系下的坐标, $P_C^W$表示相机在世界坐标系下的坐标，$P_u^C$表示像素在相机坐标系下的坐标；

卡尔曼增益K：

更新下一时刻状态，这表示的是误差增益，需要在原来基础之上加上这个增益值：

更新协方差矩阵：

完整的更新过程总结如下：
1：当视觉数据（通常是原始图像）在一定采样频率下可用时，采用一些图像处理过程来提取关键信息；
2：按照公式（7）计算残差；

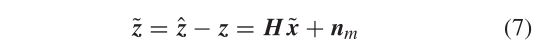
3：按照公式（8）计算卡尔曼增益K；

4：通过卡尔曼增益来更新当前状态，累加误差的形式；

5：按照公式（9）更新状态误差协方差矩阵；

3.基于优化的方法

  基于优化的方法主要依靠图像处理技术进行特征提取和图像对齐优化，而惯性测量值则被视为先验项、正则项或完全忽略。在大多数情况下，基于优化的方法有两个阶段：建图和跟踪。在建图阶段，通过各种特征检测器从图像中提取角、边等三维空间的特征。然后在两幅图像之间为检测到的所有特征定义一个重投影误差。误差作为一个损失函数被用来优化，以便找到特征或地标的坐标。在跟踪阶段，利用地图中地物和地标的坐标来定义两幅图像之间的重投影误差，并再次应用优化算法来寻找移动平台的位置和方向的变化。将估计问题分解为两个阶段的思想是为了在建图过程耗时的情况下获得快速的跟踪结果。[14,15]利用3d特征坐标和移动平台位姿变化在两幅图像之间重新投影误差来定义损失，[19]可以同时进行优化，而利用关键帧的概念可以将旧状态边缘化，从而维持一个有限的优化窗口进行实时操作。

3.1 特征对齐

  迭代非线性优化通过最小化图像中观察区域的重投影误差来寻找相机的位姿变化和特征坐标。通常，地图由若干关键帧中标识的特征组成，在这些关键帧中可以找到重要的特征。地图由一系列特征的三维坐标向量表示。当获得一个新的图像时，应该决定它是否是一个关键帧。如果是，则通过图像对齐算法计算在该新图像中发现的新特征的坐标，并与当前相机姿势一起添加到地图中。否则，地图将保持不变。

如图2所示，三维刚体变换 $T\in SE(3)$ 表示三维中的旋转和平移：


  变换矩阵$SE(3)$对应的李代数$se(3)$：$\xi =[w^T,v^T{]}^T\in R^6$,其中$w$表示旋转向量$w\in so(3)$, $v$表示平移向量$v\in R^3$,因此可得李代数$se(3)$的反对称矩阵$\Psi (\xi )$，其中$\Psi (\xi )\in R^{4\times 4}$：

已知相机内参 $\pi$，以及相机坐标系下的3D点 $P_u^C$，可以求出该点在图像坐标系下的坐标点 u：

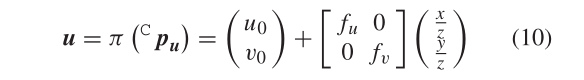
上式中$f_u,f_v$表示相机$x,y$方向上的焦距，$u_0,v_0$表示相机$x,y$方向上的平移。

其逆变换过程如下，给定图像点像素坐标 u 以及该点的深度信息 $d_u$ ，可以计算得到相机坐标系下的3D点 $P_u^C$：

定义重投影误差：

其中$\hat{z}=[\hat{u},\hat{v}{]}^T=\pi (\hat{\xi },{\hat{P}}_u^W)$表示世界坐标变换为像素坐标，即重投影后的像素坐标，$z$表示观测到的像素坐标。

所有点的重投影误差：

其中 $w$ 表示权重参数，是IMU的协方差矩阵，其中，$j$ 从1到 $m$ 是帧内关键点的索引，$i$ 是索引大小为 $n$ 的关键帧数。

最小化重投影误差，迭代求解变换矩阵 $T$:

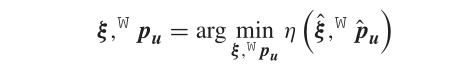
通过优化该损失函数，找到使其达到最小值时对应的 $\xi$和$P_u^W$，解决该类问题的方法也被叫做Bundle Adjustment（BA，光束平差优化）。

  在PTAM中, 优化过程被分成两个并行线程：建图和跟踪。给定跟踪结果 $\hat{\xi }$，建图线程中的优化问题是：

给定建图结果 $P_u^W$，跟踪线程中的优化问题是：

  在Levenberg-Marquardt（LM）算法中，关键是在每个迭代步骤中寻找增量 $\delta$，然后更新优化后的状态变量。$\delta$ 的解是通过：

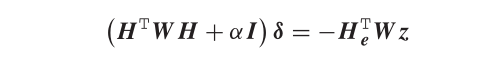
其中 $H$ 是 $z$ 的雅可比矩阵，$\alpha$ 是 $LM$ 阻尼参数， $W$是权重参数，IMU的协方差矩阵。
  在大多数情况下，只保留稀疏关键帧中的特征，以限制优化复杂度，因为优化复杂度与基于滤波的方法相同。

3.2 稠密对齐

  在上述讨论中，使用图像中特征或地标的坐标定义重投影误差。但是，它需要特征提取过程，该过程由于特征提取很少导致忽略了图像的大部分。特征提取过程往往在条件差、噪声大、鲁棒性差的环境中，因此依赖于更高层次的鲁棒性估计技术。因为所有这些估计步骤不在原始图像测量（强度）的水平上，而是系统地传播特征提取误差和累积漂移。

  另一方面，基于外观和光流的技术是基于图像的，并且直接基于原始图像测量将误差最小化[21]，即使用光度（亮度或强度）函数，因此被称为直接或密集方法。稠密方法的目的是利用整个图像进行对齐。非线性优化技术被用来寻找两个场景之间的转换。工作[22,23]通过使用Kinect RGB-D相机进行视觉里程表的图像对齐，将光度误差降至最低。

  有了RGB-D相机，例如Kinect传感器，像素的深度信息可以通过最小化每个图像中所有数据之间的距离度量函数，而不是限制特征或地标的数量，以实现多个扫描的对齐。这种稠密扫描能够重建环境中的表面场景并跟踪位姿。给定两个连续的密集深度测量，从不同角度观察同一静态场景的曲面或三维点云，可以通过获得一个点云到另一个点云的最佳映射刚性变换来估计相机位姿的变化。

  迭代最接近点（ICP）是通过优化刚性变换来匹配扫描的常用算法。ICP的工作原理是：给定两个对应的点集： β = { β 1 ， ⋅ ⋅ ⋅ ， β n } β=\{β_1，···，β_n\} β={β1​，⋅⋅⋅，βn​}和 γ = { γ 1 ， ⋅ ⋅ ⋅ ， γ n } γ=\{γ_1，···，γ_n\} γ={γ1​，⋅⋅⋅，γn​}，它们之间的平移和旋转分别是 $t和R，t和R$是通过最小化平方误差和得到：

  如果知道正确的对应关系，旋转和平移可以以闭合形式计算。如果像大多数情况一样，正确的对应关系是未知的，通常不可能一步找到最佳的相对旋转和平移。通过查找闭合点的对应关系来寻找找到对齐的迭代。如果起始位置足够接近真实变换，则ICP收敛。

3.3 惯性测量项

  IMU传感器的测量是基于滤波方法的数据驱动三维刚体运动动力学的数据源，并通过Kalman滤波与摄像机的测量数据融合。这是紧密耦合的，因为考虑了两部分之间的交叉方差。松耦合的融合是通过EKF将视觉传感器已经估计的姿态与IMU预测的姿态融合，从而保持恒定的处理时间。
  在基于优化的方法中，两个部分之间的融合也可以紧密地进行，即不需要摄像机进行明确的姿态估计。将方程（1）中IMU驱动动力学的预测结果视为高斯分布。将预测结果与真实状态之间的误差转化为协方差加权的平方误差，然后作为正则化项添加到误差函数中。根据贝叶斯推断，正则化项被视为先验概率，而图像对齐项被视为似然概率。优化后的结果是后验分布，这是由IMU先验平滑的纯图像对齐的最大似然估计结果得到的。

4.基于滤波和优化方法的联系

  在贝叶斯推理下，可以形成基于滤波和基于优化的方法。当需要近似线性化的序列时，可以通过迭代的EKF显式地建立它们的链接。当近似线性化仅为一步时，包含前向过程和后向过程的基于平滑的方法等价于通过信息矩阵的Cholesky分解求解的基于优化的方法。为了降低计算复杂度，通过只保留关键帧或滑动窗口来减少要估计的状态变量。特别地，滑动窗口方案估计将误差分为两部分，实现这两部分的一种常用方法是在一部分中优化结果，在另一部分中使用EKF边缘化最旧状态。

4.1 迭代EKF更新

  滤波法的核心是卡尔曼滤波，优化法的核心是高斯牛顿法。它们之间的联系是迭代EKF (IEKF)。EKF有两个步骤：预测和更新。设当前时刻 k 的预测步骤结果为 ${\hat{x}}_k\sim N(x_k，P_k)$， EKF与IEKF的区别在于IEKF的更新步骤中存在迭代循环，而EKF的更新步骤中只执行一个循环。在优化法中，IEKF的迭代循环能够使模型线性化引起的误差尽可能接近于相应的误差。

  下面，我们将展示IEKF更新步骤中的迭代循环与高斯牛顿优化方法(ML)的等价性。

综上所述，高斯-牛顿法的上述迭代循环被视为IEKF，其过程如下：

1：初始化状态，$i=0，u^{(0)}={\hat{x}}_{k|k-1}，P_{k|k-1}^0=P_{k|k-1}$;
2：循环计算更新状态和协方差矩阵；



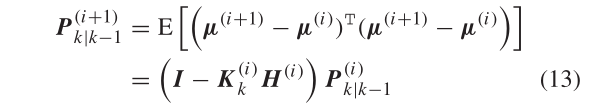
3：最终更新；

方法之间的链接。EKF、IEKF与光滑化的过程与关系。

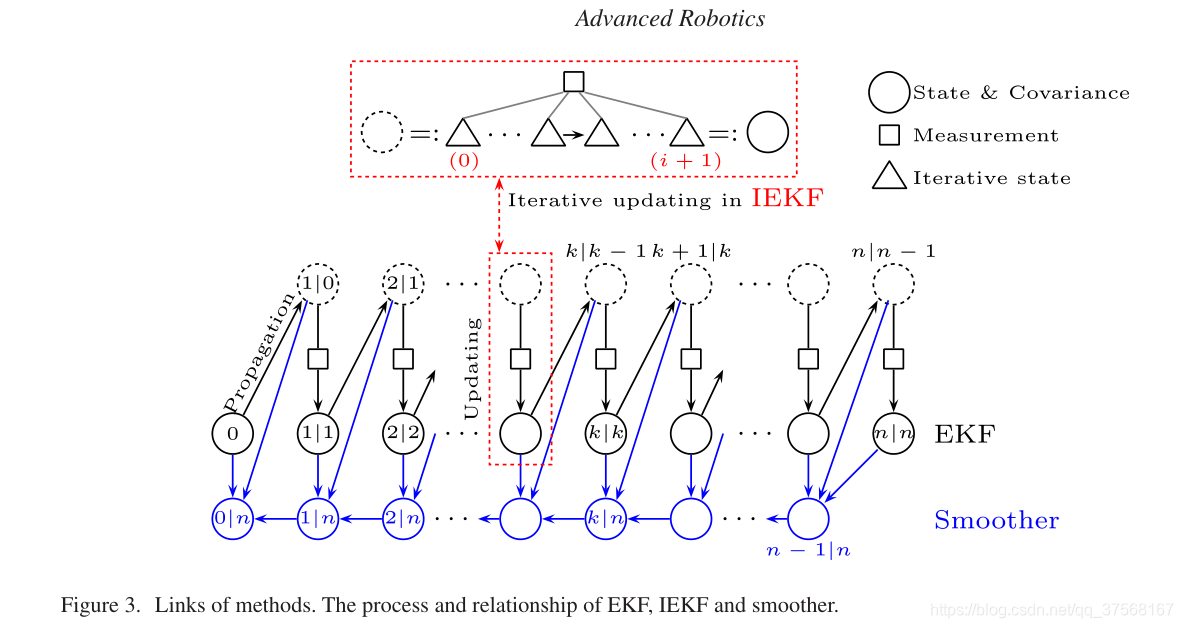
4.3 关键帧边缘化-Marginalisation

用于求解高斯牛顿方程，如下式：
$$J(x{)}^{T}J(x)\Delta x=-J(x)f(x)$$
其中$J(x)$表示雅克比矩阵，$\Delta x$表示带求解变量，$f(x)$表示误差函数；
假设，令$A=J(x{)}^{T}J(x)$，$b=-J(x)f(x)$，且其中$A$是方阵，可分块，再经过矩阵行列变换，转换为下面式子：

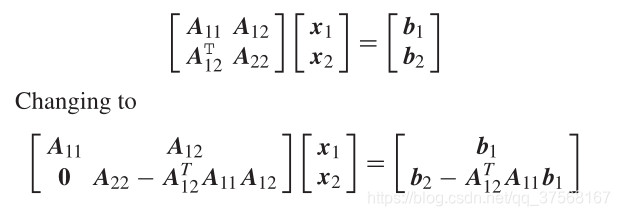
因此可以将状态 $x_1$ 边缘化，求解出状态 $x_2$，如下式：

5. 状态可观测性与参数可识别性

  VIO解决的问题是：在给定惯性和视觉传感器测量值的情况下，在线恢复全局帧中的平台轨迹。然而，从工程实现的角度来看，这个问题并不容易解决。除了滤波法和优化法的复杂性外，一些参数对于表示平台轨迹动态状态估计的成功与否也起着至关重要的作用。这些参数包括：

• 相机内参：焦距、主点和镜头畸变；
• IMU参数：加速度计和陀螺仪偏差；
• 空间参数：IMU与相机之间的转换；
• 时间参数：IMU与相机测量之间的时间延迟；

除IMU偏置和系统参数外，它们被视为时不变变量。相反，平台轨迹由时变变量表示：状态。

  通过对可观测性和可识别性的分析，仅考虑IMU和摄像机的测量值，就可以回答这些状态和参数是否可以恢复的问题。传统意义上，状态是动态变量，用可观测性分析状态估计问题，参数是静态变量，用可辨识性分析状态标定问题。利用随机游走过程对参数进行建模，可以利用可观测性(如IMU偏差)对参数进行分析。

6.结论

  本文是视觉惯性里程计(VIO)的研究现状综述。它是从两个角度提出的：基于过滤和基于优化接近。它也是通过处理视觉信号来描述的有两种方式：基于特征和基于稠密。EKF和图像对齐的广泛知识已经统一进入同一框架。两种方法之间的联系以迭代EKF、平滑化和边缘化为特征，并对两种方法进行了深入研究。分析了系统的状态可观测性和参数可辨识性。本文还总结了该领域的一系列技术，包括EKF、MAP、IEKF、BA、ICP、MHE等。今后，探索这些变体的计算复杂性将为该领域的实践者提供更直观的指导。作为这项工作的一个组成部分，应提供更多的实施细节。