准确性分析-时域法

【自控笔记】3.2 稳态误差计算

一、误差与稳态误差

通常把在阶跃输入作用下没有原理性稳态误差的系统称为“无差系统”，而把有原理性稳态误差的系统误差称为“有差系统”。

1、误差
误差可以从输入端或者输出端出发进行定义，如下图所示，按输出端定义的系统结构图只是按输入端定义结构图的等效变换，误差表现为多除以了一个H(s)。
按输出端定义的误差，比较接近理论意义上的误差，但往往不可测量。而按输入端定义的误差通常是可测量的，且具有一定的物理意义。

2、稳态误差

如下图所示，稳态误差分为静态误差和动态误差。通俗来讲，静态误差就是一个时间趋于无穷时的一个误差值，而动态误差随时间的变化而变化，是一个描述误差变化的函数。

动态误差的求解思路可以先求出E(s), 再对其进行泰勒展开，最后使用拉氏反变换求得动态误差。

二、稳态误差计算

稳态误差与自身的结构参数有关，与外作用的类型有关。稳态误差等于由输入引起的误差与由扰动引起的误差之和。

1、一般法

稳态误差是在系统稳态的前提下讨论的，所以在求解稳态误差的时候，必须先保证系统是稳定的。

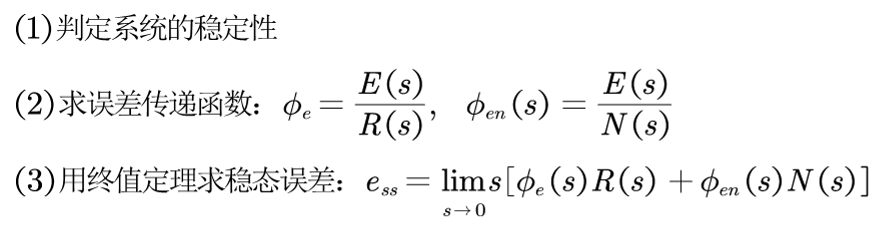
2、静态误差系数法

经过计算不同输入信号下的系统稳态误差可整理如下表格所示，记住表格的就可以快速解决问题了。

根据卢京潮老师的课程（感谢卢老师！！！），记住这个表格可以用四句话描述：
①一个系统的型别确定后，它的稳态误差随着输入“档次”的提高而增加
②当一个系统的输入确定后，它的稳态误差随着系统型别的增加而降低
③当型别与“档次”对等时，它的稳态误差是一个非0常值
④若系统的型别高而输入“档次”低，则稳态误差为0；反之为无穷。
当然也可以借助线性代数的三角矩阵记忆。

那这个表格是怎么来的呢？
我们以按输入端定义的误差（在上文）结构图来推导，如下所示：

将R(s)代入即可得到相应的稳态误差。懂得推导后，其实也不需要记住表格了，只要记住稳态误差表达式，代入输入和系统型别就好了。

2.1积分环节对系统稳态误差的影响
这里借用卢老师的一页PPT来说明积分环节对于稳态误差的影响。
如下图一个II型系统（系统稳定），开环增益为K。
①在阶跃输入下的稳态输出是一个常值，说明u(t)为零，积分才能是一个不变的常值，所以稳态误差为0。
②在速度输入下的稳态输出是一个线性函数，说明u(t)是一个常值，所以e(t)为零。
③同理，在加速度输入下，该系统的e(t)是一个常值。
④随着输入的阶数提高，这个只有两个积分环节的二阶系统不能够阻止e(t)的增大，从而稳态误差趋向于无穷。

所以积分环节体现了系统对输入信号跟随能力，每一个积分环节的输出都是对前一个输入信号的累加，
当积分环节足够时，系统输出总是以一个稳定的误差（0或者常数）对输入信号进行跟随；
当积分环节不够时，稳态误差就不再是一个常数，而是随着时间的流逝而趋于无穷了。