机械臂运动学逆解

置顶 Kkoutian吴

已于 2022-02-22 19:28:45 修改

阅读量3w

点赞数 95

分类专栏：随笔文章标签：机械臂逆解机械臂几何法逆解机械臂逆解代码 6自由度机械臂

于 2020-01-17 10:29:11 首次发布

本文链接：https://blog.csdn.net/qq_39777417/article/details/96133017

版权

随笔专栏收录该内容

1 篇文章

订阅专栏

机械臂正逆解

由于贫穷的关系，只得在淘宝上购买“玩具”机械臂进行研究，这是下面这货：
2022年2月更：之前的这个求解方式对于姿态的约束是有一些问题的，此课程包含了修正后的3、4自由度机械臂的逆解推导与源码，有兴趣的可以了解一下
在这里插入图片描述
相信小伙伴都在淘宝上买了这个手臂来玩耍，但是这手跟工业传统的6轴机械臂那差了不是一点半点。找寻了半天也没有找到现成的DH模型和运动学逆解。所有就自己使用几何法建立了模型并给出运动学逆解。最后的控制效果可以观看视频：

机械臂功能演示视频

下面是几何解过程，并附上C/C++的程序

经过我的分析，这个机械臂可以简化成一个4自由度的机械臂（夹子和夹子上的那两个舵机对运动学逆解无关），如下图：

在这里插入图片描述
画出几何示意图：

这里的j0、j1、j2、j3是指4个舵机转动的角度，L1、L2、L3指三节手臂的长度。末端执行器（夹子）中心的坐标为逆解目标 (x,y,z)。

这里值得注意的一点就是该手臂与工业6自由度的手有很大区别，工业6自由度的手的逆解目标是末端执行器的姿态加坐标，即一个齐次变换矩阵。而我们这个手按照这样来几乎很多位置都是没有解的，所有我们就剔除姿态，只保留坐标，即我们只要求我们的夹子到达这个坐标，而不需要夹子是以何种姿态到达这个坐标的。所有我们的逆解目标仅仅是个坐标而已。

这样我们容易得到正向解结果如下：

// 根据舵机角度正向解出目标坐标
	x = (L1 * sin(j1) + L2 * sin(j1 + j2) + L3 * sin(j1 + j2 + j3))*cos(j0);
	y = (L1 * sin(j1) + L2 * sin(j1 + j2) + L3 * sin(j1 + j2 + j3))*sin(j0);
	z = L1 * cos(j1) + L2 * cos(j1 + j2) + L3 * cos(j1 + j2 + j3);

这里我们可以看出，我们的输入是j0、j1、j2、j3这四个舵机转动的角度，而我们的目标只是一个三维坐标(x,y,z)。
逆解就是输入坐标（x,y,z）,然后求j0、j1、j2、j3，但是我们逆向求解的时候就可能会出现多组解（未知数的个数4大于方程的个数3）。这样的话我们就只能先确定一个未知数的取值，然后才能对方程进行求解。

底座舵机j0的最好算：

j0 = atan2(y, x);

这里我采取的是先确定j1的值，然后再求解方程（这里方程的推导我就不写啦，直接上代码，代码里就是我解出来的结果）。但是我们所确定的这个j1的值不一定能求出解，也可能求出几组解。所有我们就将j1舵机所能到达的角度都取一遍，保证能求出更多的解。

	for (j1 = -90; j1 < 90; j1++)//先确定j1的值，并且把j1从-90°到90°都取一遍，算出所有有可能的解
	{
		j1 *= RAD2ANG;//弧度转换
		j3 = acos((pow(a, 2) + pow(b, 2) + pow(L1, 2) - pow(L2, 2) - pow(L3, 2) - 2 * a*L1*sin(j1) - 2 * b*L1*cos(j1)) / (2 * L2*L3));
		//确定j1的角度后，就可以求出j3的角度。
		m = L2 * sin(j1) + L3 * sin(j1)*cos(j3) + L3 * cos(j1)*sin(j3);
		n = L2 * cos(j1) + L3 * cos(j1)*cos(j3) - L3 * sin(j1)*sin(j3);
		t = a - L1 * sin(j1);
		p = pow(pow(n, 2) + pow(m, 2), 0.5);
		q = asin(m / p);
		j2 = asin(t / p) - q;
		//接着就可以求出j2的角度。
		//求出4个角度后，我们先验算一遍这4个角度求出的值（x1,y1,z1）和我们的目标坐标（x,y,z）是否一致
		x1 = (L1 * sin(j1) + L2 * sin(j1 + j2) + L3 * sin(j1 + j2 + j3))*cos(j0);
		y1 = (L1 * sin(j1) + L2 * sin(j1 + j2) + L3 * sin(j1 + j2 + j3))*sin(j0);
		z1 = L1 * cos(j1) + L2 * cos(j1 + j2) + L3 * cos(j1 + j2 + j3);
		j1 = ANG2RAD(j1);
		j2 = ANG2RAD(j2);
		j3 = ANG2RAD(j3);
		//输出误差小于1cm的解，并输出该解的正向解目标
		if(x1<(x+1) && x1 > (x-1) && y1<(y + 1) && y1 >(y - 1) && z1<(z + 1) && z1 >(z - 1))
		{
			printf("j1:%f,j2:%f,j3:%f,x:%f,y:%f,z:%f\r\n", j1, j2, j3, x1, y1, z1);
		}
	}

可执行的完整C++代码如下（直接复制这个用，上面的代码是过程讲解）：

#include "pch.h"
#include <iostream>
#include <stdio.h>
#include <math.h>

#define RAD2ANG (3.1415926535898/180.0)
#define ANG2RAD(N) ( (N) * (180.0/3.1415926535898) )
void inverseKinematics(double x, double y, double z);

int main()
{
	inverseKinematics(0, 30, 0);//逆解目标为（0，30，0）这个坐标

}

void inverseKinematics(double x, double y, double z)
{
	double a, b, c; //临时变量
	double L1 = 10, L2 = 11, L3 = 14;//3节手臂的长度
	double m, n, t, q, p;//临时变量
	double j1, j2, j3, j0;//4个舵机的旋转角度
	double x1, y1, z1;//逆解后正解算出来的值，看是否与逆解值相等
	char i = 0;
	j0 = atan2(y, x);
	a = x / cos(j0);
	if (x == 0) a = y; //如果x为0，需要交换x，y
	b = z;

	for (j1 = -90; j1 < 90; j1++)
	{
		j1 *= RAD2ANG;
		j3 = acos((pow(a, 2) + pow(b, 2) + pow(L1, 2) - pow(L2, 2) - pow(L3, 2) - 2 * a*L1*sin(j1) - 2 * b*L1*cos(j1)) / (2 * L2*L3));
		//if (abs(ANG2RAD(j3)) >= 135) { j1 = ANG2RAD(j1); continue; }
		m = L2 * sin(j1) + L3 * sin(j1)*cos(j3) + L3 * cos(j1)*sin(j3);
		n = L2 * cos(j1) + L3 * cos(j1)*cos(j3) - L3 * sin(j1)*sin(j3);
		t = a - L1 * sin(j1);
		p = pow(pow(n, 2) + pow(m, 2), 0.5);
		q = asin(m / p);
		j2 = asin(t / p) - q;
		//if (abs(ANG2RAD(j2)) >= 135) { j1 = ANG2RAD(j1); continue; }
		/***************计算正解然后与目标解对比，看解是否正确**************/
		x1 = (L1 * sin(j1) + L2 * sin(j1 + j2) + L3 * sin(j1 + j2 + j3))*cos(j0);
		y1 = (L1 * sin(j1) + L2 * sin(j1 + j2) + L3 * sin(j1 + j2 + j3))*sin(j0);
		z1 = L1 * cos(j1) + L2 * cos(j1 + j2) + L3 * cos(j1 + j2 + j3);
		j1 = ANG2RAD(j1);
		j2 = ANG2RAD(j2);
		j3 = ANG2RAD(j3);
		if (x1<(x + 1) && x1 >(x - 1) && y1<(y + 1) && y1 >(y - 1) && z1<(z + 1) && z1 >(z - 1))
		{
			printf("j0:%f,j1:%f,j2:%f,j3:%f,x:%f,y:%f,z:%f\r\n", ANG2RAD(j0), j1, j2, j3, x1, y1, z1);
			i = 1;
		}
	}
	for (j1 = -90; j1 < 90; j1++)//这个循环是为了求解另一组解，j2 = asin(t / p) - q;j2 = -(asin(t / p) - q);多了个负号
	{
		j1 *= RAD2ANG;
		j3 = acos((pow(a, 2) + pow(b, 2) + pow(L1, 2) - pow(L2, 2) - pow(L3, 2) - 2 * a*L1*sin(j1) - 2 * b*L1*cos(j1)) / (2 * L2*L3));
		//if (abs(ANG2RAD(j3)) >= 135) { j1 = ANG2RAD(j1); continue; }
		m = L2 * sin(j1) + L3 * sin(j1)*cos(j3) + L3 * cos(j1)*sin(j3);
		n = L2 * cos(j1) + L3 * cos(j1)*cos(j3) - L3 * sin(j1)*sin(j3);
		t = a - L1 * sin(j1);
		p = pow(pow(n, 2) + pow(m, 2), 0.5);
		q = asin(m / p);
		j2 = -(asin(t / p) - q);
		//if (abs(ANG2RAD(j2)) >= 135) { j1 = ANG2RAD(j1); continue; }
		x1 = (L1 * sin(j1) + L2 * sin(j1 + j2) + L3 * sin(j1 + j2 + j3))*cos(j0);
		y1 = (L1 * sin(j1) + L2 * sin(j1 + j2) + L3 * sin(j1 + j2 + j3))*sin(j0);
		z1 = L1 * cos(j1) + L2 * cos(j1 + j2) + L3 * cos(j1 + j2 + j3);
		j1 = ANG2RAD(j1);
		j2 = ANG2RAD(j2);
		j3 = ANG2RAD(j3);
		if (x1<(x + 1) && x1 >(x - 1) && y1<(y + 1) && y1 >(y - 1) && z1<(z + 1) && z1 >(z - 1))
		{
			printf("j0:%f,j1:%f,j2:%f,j3:%f,x:%f,y:%f,z:%f\r\n", ANG2RAD(j0), j1, j2, j3, x1, y1, z1);
			i = 1;
		}
	}

	if (i == 0)printf("无解");

}

输出结果如下图：
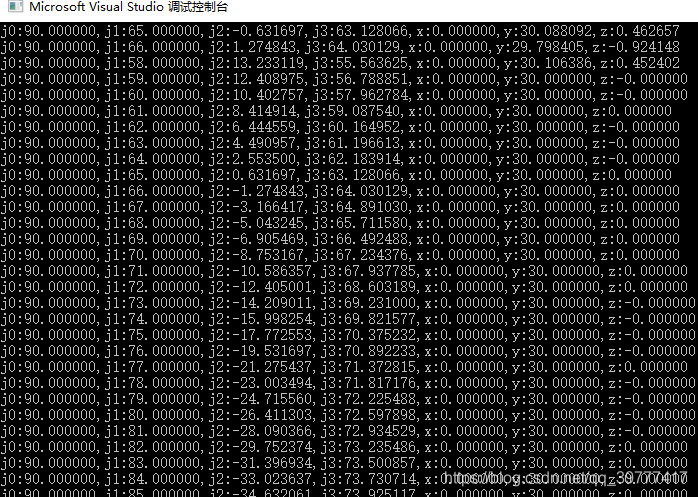
在这里插入图片描述

然后我们就可以根据我们的需求选择我们的解，如果只是简单抓取地面上的东西，就选择夹子向下且最接近垂直的那个解，即j3最接近90的那个解，这个解最适合夹取地面上的东西。如果是像视频中倒水一样，就得选择夹子为水平的解，具体是个什么约束关系你们可以自己推一推。反正你可以自由选择解。
2022年2月更：之前的这个求解方式对于姿态的约束是有一些问题的，此课程包含了修正后的3、4自由度机械臂的逆解推导与源码，有兴趣的可以了解一下

最后大家有不懂或者有更好建议的请加我

机械臂基础入门图文教程1
机械臂基础入门图文教程2
机械臂基础入门图文教程3
控制该机械臂的视频教程与源码、包括机械臂系统从上到下的梳理、机械臂的硬件、通讯与控制

QQ:965295412 WX：15310294950