0 总述
DTW可以计算两个时间序列的相似度,尤其适用于不同长度、不同节奏的时间序列(比如不同的人读同一个词的音频序列)
DTW将自动扭曲(warping)时间序列(即在时间轴上进行局部的缩放),使得两个序列的形态尽可能的一致,得到最大可能的相似度。
DTW采用了动态规划的方法来进行时间规整的计算
1 欧几里得距离的局限性
描述两个序列之间的相似性,欧氏距离是一种十分简单且直观的方法,但对于序列之间步调不统一的情况,计算欧氏距离得到的结果会比实际的最小距离大很多,比如下面两个几乎一样的序列:

·
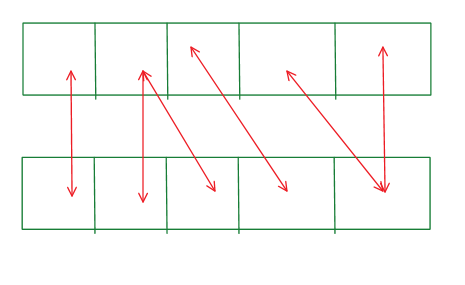
左边是欧氏距离的对应关系,在同一时刻上的点相互对应,计算总距离;右边是DTW的点对应关系。
可以看到,下面序列某时刻的点可以对应上面序列非同一时刻的点;同时一个点可以对应多个点;多个点也可以对应一个点,也就是说每个点尽可能找离它距离最小的点,允许时间轴上的伸缩。
显而易见的,这种情况下DTW计算的距离比欧氏距离更小。因此对于时间上有拉伸或压缩的序列,使用DTW计算的序列距离更加合理。
该算法在语音序列匹配中使用十分广泛。
2 DTW 算法
假设我们有两个时间序列Q和C,他们的长度分别是n和m(n和m不一定相等),我们记为:
现在我们需要将两个序列对齐,DTW采用动态规划的方法进行对齐。
为了对齐这两个序列,我们需要构造一个n*m的矩阵网络,矩阵元素(i,j)表示
和
两个点之间的距离

【不同的应用问题中,会有不同的d】
【一般采用欧氏距离,
】
【在有些问题中,这个距离又被称作失真度】
DTW算法旨在寻找一条通过此网络中若干个点的一条路径,路径中的经过的点即为两个序列之间进行计算所需要的对齐的点
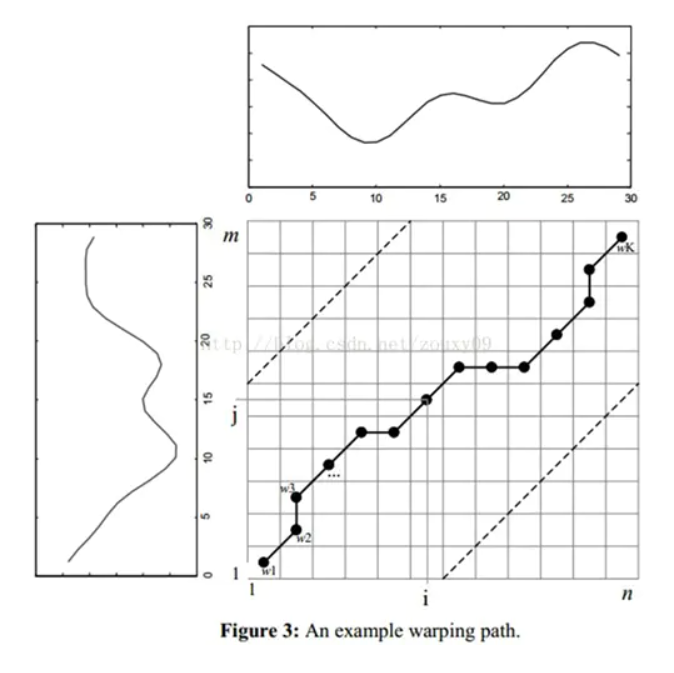
但是,这条路径并不是随意选择的,它需要满足几个约束条件:
- 边界条件【
,
】,首尾需要对齐
- 连续性+单调性【如果
,那么对于路径上的下一个点
,需要满足
,
】【也就是路径只能连接正上方、正右方、右上方三个相邻点钟的一个】【
】——>保证两个要比较的序列Q和C中的每一个坐标都会在W中出现
我们的目的是最小化路径上的值,即
【有时候也没有这个K)
分母中的K主要是用来对不同的长度的规整路径做补偿。因为不同的路径其长短不同,较长的路径有较多的“点对”,会有较多的距离累加上去,所以总距离除以K得到单位路径的距离。
3 DTW 举例
比如我们有两个序列
import matplotlib.pyplot as plt import numpy as np a=np.array([1,3,2,4,2]) b=np.array([0,3,4,2,2]) plt.plot(a) plt.plot(b)
他们之间的欧氏距离为
np.sqrt(np.sum((a-b)*(a-b)) #3
使用DTW的话,先要计算两个序列之间的欧氏距离
a-b 0 3 4 2 2 1 1 2 3 1 1 3 3 0 1 1 1 2 2 1 2 0 0 4 4 1 0 2 2 2 2 1 2 0 0
使用动态规划的话,就需要有这样的状态转移方程:
其中d(i,j)就是第(i,j)个条目里面的内容,也就是ai和bj之间的欧几里得距离
| a-b | 0 | 3 | 4 | 2 | 2 |
| 1 | 1 dp(0,0) =d(0,0) =1 | 2 dp(0,1) =dp(0,0)+d(0,1) =1+2=3 | 3 dp(0,2) =dp(0,1)+d(0,2) =3+3=6 | 1 dp(0,3) =dp(0,2)+d(0,3) =6+1=7 | 1 dp(0,4) =dp(0,3)+d(0,4) =7+1=8 |
| 3 | 3 dp(1,0) =dp(0,0)+d(1,0) =1+3=4 | 0 dp(1,1) =min(dp(0,0) ,dp(1,0) ,dp(0,1)) +d(1,1) =1+0=1 | 1 dp(1,2) =min(dp(0,1) ,dp(1,1) ,dp(0,2)) +d(1,2) =1+1=2 | 1 dp(1,3) =min(dp(0,2) ,dp(1,2) ,dp(0,3)) +d(1,3) =2+1=3 | 1 dp(1,4) =min(dp(0,3) ,dp(1,3) ,dp(0,4)) +d(1,4) =3+1=4 |
| 2 | 2 dp(2,0) =dp(1,0)+d(2,0) =4+2=6 | 1 dp(2,1) =min(dp(1,0) ,dp(2,0) ,dp(1,1)) +d(2,1) =1+1=2 | 2 dp(2,2) =min(dp(1,1) ,dp(2,1) ,dp(1,2)) +d(2,2) =1+2=3 | 0 dp(2,3) =min(dp(1,2) ,dp(2,2) ,dp(1,3)) +d(2,3) =2+0=2 | 0 dp(2,4) =min(dp(1,3) ,dp(2,3) ,dp(1,4)) +d(2,4) =2+0=2 |
| 4 | 4 dp(3,0) =dp(2,0)+d(3,0) =6+4=10 | 1 dp(3,1) =min(dp(2,0) ,dp(3,0) ,dp(2,1)) +d(3,1) =2+1=3 | 0 dp(3,2) =min(dp(2,1) ,dp(3,1) ,dp(2,2)) +d(3,2) =2+0=2 | 2 dp(3,3) =min(dp(2,2) ,dp(3,2) ,dp(2,3)) +d(3,3) =2+2=4 | 2 dp(3,4) =min(dp(2,3) ,dp(3,3) ,dp(2,4)) +d(3,4) =2+2=4 |
| 2 | 2 dp(4,0) =dp(3,0)+d(4,0) =10+2=12 | 1 dp(4,1) =min(dp(3,0) ,dp(4,0) ,dp(3,1)) +d(4,1) =3+1=4 | 2 dp(4,2) =min(dp(3,1) ,dp(4,1) ,dp(3,2)) +d(4,2) =2+2=4 | 0 dp(4,3) =min(dp(3,2) ,dp(4,2) ,dp(3,3)) +d(4,3) =2+0=2 | 0 dp(4,4) =min(dp(3,3) ,dp(4,3) ,dp(3,4)) +d(4,4) =2+0=2 |
计算出所有的dp值之后,就可以得到它的DTW值,也即2
也就是这样的一个对应关系
4 python 实现
dtw_lst=[[-1 for _ in range(len(b))] for _ in range(len(a))]
#DTW矩阵,也就是上例中的dp(i,j)
def dist(i,j):
return(math.fabs(a[i]-b[j]))
#两个点之间的欧几里得距离
dtw_lst[0][0]=dist(0,0)
def DTW(i,j):
if(dtw_lst[i][j]!=-1):
return(dtw_lst[i][j])
#表示之前已经计算过这一对(i,j)的dtw了
else:
dtw_prev=np.inf
if(i!=0):
dtw_prev=min(dtw_prev,DTW(i-1,j))
if(j!=0):
dtw_prev=min(dtw_prev,DTW(i,j-1))
if(i!=0 and j!=0):
dtw_prev=min(dtw_prev,DTW(i-1,j-1))
#由于不知道有没有左上,左,和上的点,所以需要讨论
dtw_lst[i][j]=dtw_prev+dist(i,j)
return(dtw_lst[i][j])
DTW(len(a)-1,len(b)-1)
#2.0和手推的结果是一样的
5 DTW不是一个有效的距离
DTW满足以下性质:

然而,DTW不满足三角不等式,因而它不是一个有效的距离
6 DTW的问题
6.1 singularity(奇点)问题
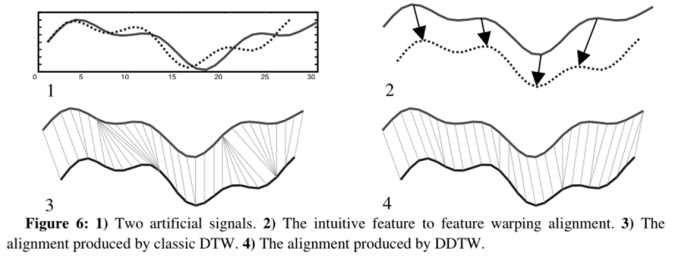
- 有时 DTW 会在对齐时产生不自然的扭曲/翘曲

- A 中实线、虚线所展示的是两条合成信号(均值、方差都相同)
- B 中展示的是自然的“feature to feature”的对应
- C 中展示的则是 DTW 的结果。
- 不难发现,DTW 没能自然地将图形中的波峰与波峰相对应,反而产生了一个序列中的一个点对应另外一个序列中的多个点的情况,这种情况被称为“Singularities”(奇点)
- 出现这种情况的原因是 DTW 算法试图通过扭曲 X 轴来解释 Y 轴上的变化。
6.2 解决奇点问题的方法
6.2.1 windowing
- 奇点问题的出现是因为两个时间序列上相隔很远的点仅因为值相同/相近,而易被 warping 到一起
- ——>可以限制 DTW 在 warping 过程中的能选择的范围来解决奇点问题
- 具体可以通过设置一个 warping window 来实现
- n和m分别是i和j对应的时间序列的长度
- R是warping window 的大小
- 第2节“Figure 3”中的两条虚线所夹范围就是经过warping window限制之后的范围,DTW的warping path只能在这个区域内
6.2.2 slope weighting
之前的DTW是:
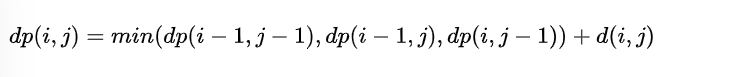
现在对它进行一定的调整:
- 调整的地方是在min函数的后两项中加入了一个正实数X
- 对X进行调整可以使得warping path的方向(即slope)有一定的偏好和调整
- 比如X值较大时,warping path会更多地选择对角线朝向
- 对X进行调整可以使得warping path的方向(即slope)有一定的偏好和调整
6.2.3 step pattern
之前的DTW是:
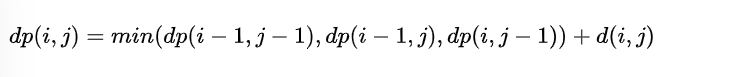

现在改成

6.3 上述解决奇点问题方法的局限性
- 6.2中的几种解决方案在一定程度上对解决奇点问题有一定帮助,然而,它们仍然存在以下缺点:
- 有可能错过正确的 warping path
- 上述解决方法都是人为地对 warping path 进行限制和调整,来减少翘曲
- ——>这很有可能会错过真正正确的 warping path
- 参数的选择没有明确的指导,需要人为调参
- 有可能错过正确的 warping path
7 DDTW(derivative DTW)
- DTW之所以会造成奇点问题,本质原因是DTW算法只考虑每一时刻单个数值的值(两个时间序列的两个点qi和cj之间的距离)
- 但是,如果两个数值相同的数据点,一个位于时间序列的上升趋势部分,一个位于时间序列的下降趋势部分,对于DTW来说,因为他们数值一样,很容易被匹配到一起。这便导致了奇点问题
- DDTW每个时刻考虑的不是数值的取值,而是时间序列数据的形状,即该时刻对应的一阶导数
- 两个时间序列,在两个时刻的一阶导数差值的平方
- DDTW中使用如下方式估计一阶导数

- 在qi点处一阶导数的估计——>通过qi和
这两个点的斜率、通过
这两个点的斜率 的平均值
- ——>这种估计方式对outliner更稳定
- 第一个和最后一个点用上述公式是没法估计的,DDTW用如下方式近似:
- 两个时间序列,在两个时刻的一阶导数差值的平方
8 WDTW
- 在计算两个序列上的两个点之间欧氏距离时加上一个 weight,而这个 weight 与两个点之间的 X 轴上的距离有关系

- p=2——>计算两个点ai和bj的欧氏距离
——>两个点在X轴上的距离相关的weight权重
- 当|i-j|的值较大(两个点在X轴上距离比较远)时,
较大,此时ai和bj距离就会被放大,被WDTW匹配在一起的概率被减小
- 当
是一个常数的时候,此时WDTW对任何(i,j)对的惩罚时相同的,此时WDTW退化为DTW
-
当
的数值很大时,此时WDTW对任何(i,j)对的惩罚都很大【甚至第i个点和第i+1个点的匹配也不行】。此时WDTW退化为欧几里得距离
- 当|i-j|的值较大(两个点在X轴上距离比较远)时,
参考资料










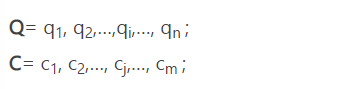




















 1179
1179

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










