算法笔记：匈牙利算法

1 二部图（二分图）

• 二分图（Bipartite graph）是一类特殊的图，它可以被划分为两个部分，每个部分内的点互不相连。
  • 
  • 匈牙利算法主要用来解决两个问题：求二分图的最大匹配数和最小点覆盖数。

2 最大匹配问题

2.1 问题描述

•  左右有两个点集，我们最多可以找到多少条没有公共端点的边？

2.2 匈牙利算法举例

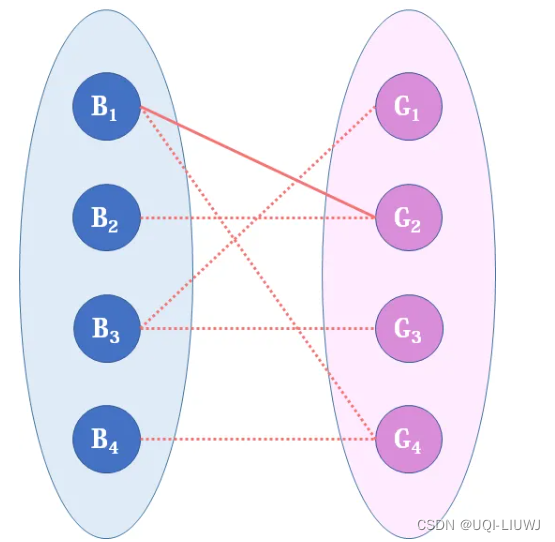
• 从B1开始，从G1~G4一个一个遍历过去
  • 首先遍历到和B1有连边的G2
  • 暂时把B1和G2连接
    • 
• 接着看B2，也从G1~G4一个一个遍历过去
  • 首先遍历到和B2有连边的G2
  • 此时G2已经和左边的B1连接了
  • 于是倒回去看B1，看看B1有没有别的可以连接的选项
  • 发现B1在G2后还可以连接G4
  • ——>B2暂时连G2，B1暂时连G4
  • 
• 接着看B3，首先B3会先遍历到G1
  • G没啥冲突
• 最后看B4
  • B4遍历到G4
  • G4此时连着B1
    • B1没有别的可以连接的了
  • ——>B4没法连G4

 2.3        Python实现

2.3.1 数据和准备部分

# 左点-右点--邻接矩阵
ada_matrix=[[0,1,0,1],
           [0,1,0,0],
           [1,0,1,0],
           [0,0,0,1]]

num_left=len(ada_matrix)
num_right=len(ada_matrix[0])

right_pair=[-1]*num_right
#右点和哪个左点匹配了（一开始都是-1，表示没有匹配）

2.3.2 if_match 函数

• 表示左点匹配到i的时候，根据right_visited的情况，左点i是否会匹配一个右点
• right_visited表示匹配左点i的过程中，每个右点是否被考虑过

def if_match(i):
    global right_visited
    for j in range(num_right):
        if(ada_matrix[i][j]==1 and right_visited[j]==0):
            #如果右边的点和左边的点有连边；同时在考虑左点i的过程中，右点j没有被考虑过
            
            right_visited[j]=1
            
            if(right_pair[j]==-1):
                #如果左边的点现在还没有右边的点和他匹配，那么左点i和右点j连接
                right_pair[j]=i
                return True
                #左点遍历到i的时候，暂时可以匹配j（后续i点可能需要“改嫁”，但是如果只遍历到i，是不冲突的）
            elif(if_match(right_pair[j])):
                 right_pair[j]=i
                 #如果左边的点已经和别的点(right_pair[j])匹配了，那么看看(right_pair[j])能不能“改嫁”
                 #也就是看看不能选择j的情况下，(right_pair[j])能不能匹配到其他的右点
                    
                 #这是一个递归过程，进行if_match(right_pair[j])的时候，假设匹配到新的右点j'
                 #又需要判断j'是否有点和它匹配+如果匹配了，已经匹配的点能不能“改嫁”
                
                 return True
                 #左点遍历到i的时候，暂时可以匹配j（后续i点可能需要“改嫁”，但是如果只遍历到i，是不冲突的）
    return False                

2.3.3 主函数

for i in range(num_left):
    #每一个左边的点
    global right_visited
    right_visited=[0]*num_right
    #在考虑左边的点i的时候，右边的点有没有被考虑过
    print(right_pair)
    if_match(i)


'''
[-1, -1, -1, -1]
[-1, 0, -1, -1]
[-1, 1, -1, 0]
[2, 1, -1, 0]
'''

结果和前面的手动推导是一样的

3 最小点覆盖问题

• 找到最少的一些点，使二分图所有的边都至少有一个端点在这些点之中。
• 倒过来说就是，删除包含这些点的边，可以删掉所有边
• 
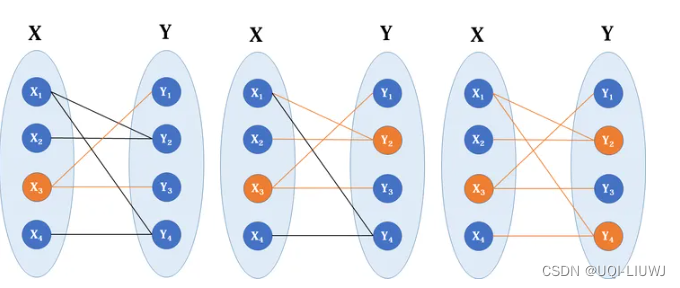
• König定理：一个二分图中的最大匹配数等于这个图中的最小点覆盖数

参考内容：带你入门多目标跟踪（三）匈牙利算法&KM算法 - 知乎 (zhihu.com)