C++代码
//要实现平滑二维曲线的算法,你可以使用贝塞尔曲线或B样条曲线。下面是一个使用B样条曲线的C++算法的示例:
#include <iostream>
#include <vector>
#include <fstream>
#include <iomanip>
#include <string>
struct Point {
double x;
double y;
};
std::vector<Point> SmoothCurve(std::vector<Point>& points) {
std::vector<Point> smoothedPoints;
// 添加开始点
smoothedPoints.push_back(points.front());
// 计算内插点
for (int i = 1; i < points.size() - 1; i++) {
Point p0 = points[i - 1];
Point p1 = points[i];
Point p2 = points[i + 1];
// 在这里使用具体的B样条曲线算法进行内插计算
// 这里使用简化示例,线性插值
Point interpolatedPoint;
interpolatedPoint.x = (p0.x + p1.x + p2.x) / 3.0;
interpolatedPoint.y = (p0.y + p1.y + p2.y) / 3.0;
smoothedPoints.push_back(interpolatedPoint);
}
// 添加结束点
smoothedPoints.push_back(points.back());
return smoothedPoints;
}
int main() {
double x[69] = {-3.7961,-3.7461,-3.6961,-3.6461,-3.5961,-3.5461,-3.4961,-3.4461,-3.3961,-3.3461,-3.2961,-3.2461,-3.1961,
-3.1461,-3.0961,-3.0461,-2.9961,-2.9461,-2.8961,-2.8461,-2.7961,-2.7461,-2.6961,-2.6461,-2.5961,-2.5461,-2.4961,
-2.4461,-2.3961,-2.3461,-2.2961,-2.2461,-2.1961,-2.1461,-2.0961,-2.0461,-1.9961,-1.9461,-1.8961,-1.8461,-1.7961,-1.7461,-1.6961,-1.6461,-1.5961,
-1.5461,-1.4961,-1.4461,-1.3961,-1.3461,-1.2961,-1.2461,-1.1961,-1.1461,-1.0961,-1.0461,-0.9961,-0.9461,-0.8961,-0.8461,-0.7961,-0.7461,-0.6961,-0.6461,-0.5961,
-0.5461,-0.4961,-0.4961,-0.4961};
double y[69]= {-0.5775,-0.5775,-0.5775,-0.5775,-0.5775,-0.5775,-0.5775,-0.5775,-0.5775,-0.5775,-0.5775,-0.6275,
-0.6775,-0.7275,-0.7775,-0.8275,-0.8775,-0.9275,-0.9775,-1.0275,-1.0775,-1.1275,-1.1775,-1.2275,-1.2275,
-1.2775,-1.2775,-1.2775,-1.3275,-1.3275,-1.3275,-1.3275,-1.3275,-1.3275,-1.3275,-1.3275,-1.3275,-1.3275,-1.3275,
-1.3275,-1.3275,-1.3275,-1.3275,-1.3275,-1.2775,-1.2775,-1.2775,-1.2275,-1.2275,-1.2275,-1.2275,-1.2275,-1.1775,-1.1275,
-1.0775,-1.0275,-0.9775,-0.9275,-0.8775,-0.8275,-0.8275,-0.7775,-0.7775,-0.7275,-0.6775,-0.6275,-0.5775,-0.5775,-0.5775};
// std::vector<Point> path;
// 添加30个路径点的x和y坐标
// 示例点集
std::vector<Point> points;
for(int i = 0;i < 69;i++){
points.push_back({ x[i], y[i] });
}
std::vector<Point> smoothedPoints = SmoothCurve(points);
// 输出平滑后的点集
for (const auto& point : smoothedPoints) {
std::cout << point.x << " " << point.y << " " << std::endl;
std::ofstream file;
file.open("/home/juchunyu/20231013/240218/log.txt",std::ios::app);
if(file.is_open()){
file<< point.x << " " << point.y << std::endl;
}
file.close();
}
return 0;
}
这段代码实现了一种简化的平滑曲线算法,使用线性插值来平滑给定路径上的点。下面是该代码的原理解释:
-
创建一个空的
smoothedPoints向量,用于存储平滑后的路径点。 -
在
smoothedPoints向量中添加输入points的起始点。 -
遍历输入
points中除了起始点和终止点之外的所有点。 -
对于每个点,我们考虑路径上的前一个点
p0、当前点p1和后一个点p2。 -
使用一种内插算法(在这里是线性插值)来计算
p0、p1和p2之间的一个内插点。这个内插点的坐标是前一个点、当前点和后一个点的坐标的平均值。 -
将计算得到的内插点添加到
smoothedPoints向量中。 -
在
smoothedPoints向量中添加输入points的终止点。 -
返回平滑后的路径点
smoothedPoints向量。
请注意,这里的内插算法是一个简化示例,使用了线性插值来平滑路径上的点。实际应用中,你可以使用更复杂的算法,如B样条曲线、Catmull-Rom曲线等。这些算法可以根据需要,根据控制点和参数来计算平滑曲线。希望这个解释对你有所帮助!如果有任何进一步的问题,请随时提问。
效果
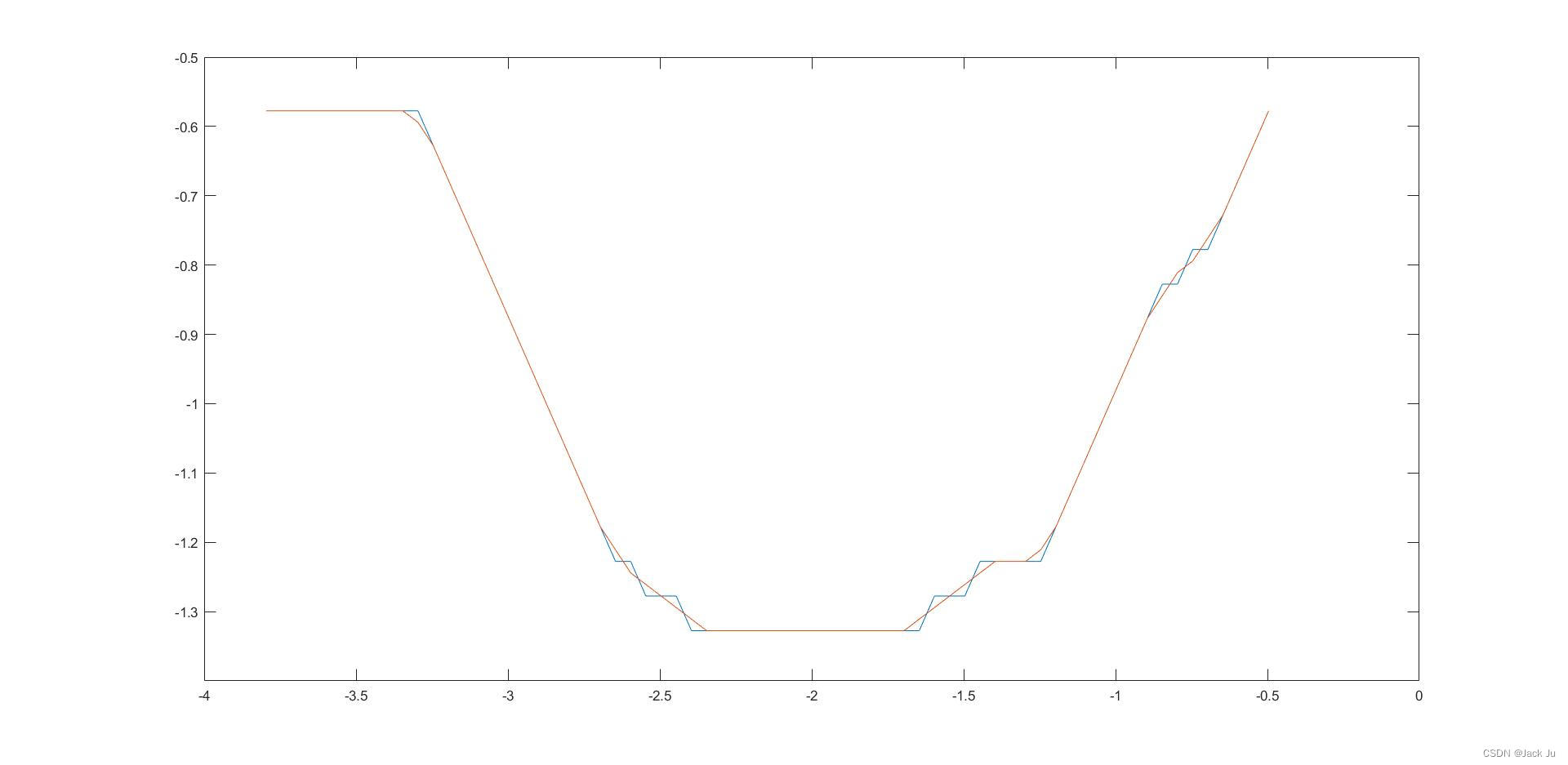
蓝色是原始路径,红色是平滑后的曲线。










 本文介绍了如何使用C++通过线性插值算法来平滑机器人路径点。首先创建一个向量存储平滑路径,然后通过遍历路径点,计算每个点与前后点的内插点并添加到向量中,最终形成平滑曲线。实际应用中,还可以考虑采用更复杂的平滑算法,如B样条曲线或Catmull-Rom曲线。
本文介绍了如何使用C++通过线性插值算法来平滑机器人路径点。首先创建一个向量存储平滑路径,然后通过遍历路径点,计算每个点与前后点的内插点并添加到向量中,最终形成平滑曲线。实际应用中,还可以考虑采用更复杂的平滑算法,如B样条曲线或Catmull-Rom曲线。

















 1756
1756

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










