precision(精确率)和recall(召回率)的计算
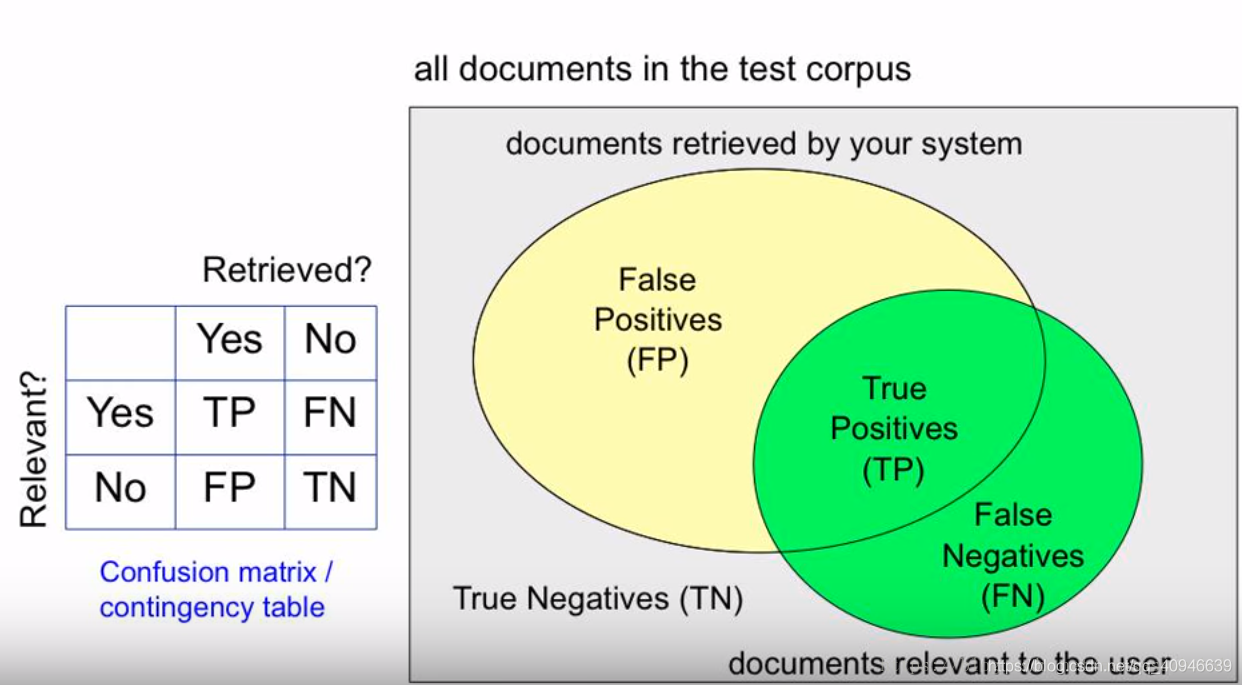
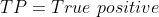 (模型预测为正样本,实际为正样本)
(模型预测为正样本,实际为正样本)
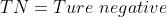 (模型预测为负样本,实际为负样本)
(模型预测为负样本,实际为负样本)
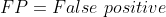 (模型预测为正样本,实际为负样本)
(模型预测为正样本,实际为负样本)
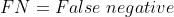 (模型将预测为负样本,实际为正样本)
(模型将预测为负样本,实际为正样本)
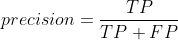 正确预测的正样本除以被判为正样本(正确判断为正样本的样本和误判为正样本的样本)的比例之和
正确预测的正样本除以被判为正样本(正确判断为正样本的样本和误判为正样本的样本)的比例之和
 正确预测的样本和所有正样本的比列
正确预测的样本和所有正样本的比列
其次,我们需要知道的precision与recall基本成反比的,precison很高则recall会很低,反之,recall会很高。
为什么会这样呢,对于一组我们准备好了的样本(即已知了正样本和负样本情况),之后我们使用模型去对样本进行检测从而得到该样本相对正样本(该模型的检测正样本的)的置信度。我们通过控制置信度 来调整recall的值,置信度大于等于
来调整recall的值,置信度大于等于 的,我们认为这个样本是正样本。对于一个已知的样本,其实际正样本数(TP+FN)是已知的。调整置信度会让模型检测出的正确的正样本数变化,从而使recall变化。随着置信度的调低,检测出正确的正样本数会越来越来多,而总的召回率(recall)在不断提高,而precision会不断降低。
的,我们认为这个样本是正样本。对于一个已知的样本,其实际正样本数(TP+FN)是已知的。调整置信度会让模型检测出的正确的正样本数变化,从而使recall变化。随着置信度的调低,检测出正确的正样本数会越来越来多,而总的召回率(recall)在不断提高,而precision会不断降低。
关于随着recall增大,precision为什么降低,我的观点是模型是用来检测正样本的,所有当我们将置信度从高到低往下排列时,正样本数是集中序列的前面的,因此随着recall增大,precision会减少。
这个连接里面有一个例子,结合我的讲解和这个例子,MAP值应当会更好理解。
https://www.jianshu.com/p/82be426f776e
AP(average precision)是什么?
关于AP的计算,我们参考PASCAL VOC CHALLENGE的计算方法。
我们让recall在[0,1]里从0开始取值,步长为0.1,则最终有十一个recall值,AP就是由这十一不同recall阶层precision的评价值而得到
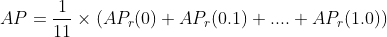
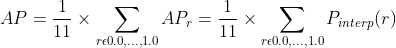
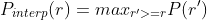
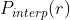 是超过r的recall中对应最大的precision值,例如p_interp(0.6)就是大于0.6的所有recall中对应的最大的precision的值
是超过r的recall中对应最大的precision值,例如p_interp(0.6)就是大于0.6的所有recall中对应的最大的precision的值
MAP值是不同类别的AP值的均值
自2010年,PASCAL VOC CHANLLNEGE换了另一种算法。
新的计算方法假设这N个样本中有M个正例,那么我们会得到M个recall值(1/M,2/M....M/M),对于每个recall值r,我们可以计算出对应( >r)的最大precision,然后对这M个precision值取平均即得到最后AP值。
>r)的最大precision,然后对这M个precision值取平均即得到最后AP值。
MAP的题外话:
MAP相对于precision、Recall是能够反映全局性能的指标。
,如果一个系统的性能较好,其曲线应当尽可能的向上突出。
更加具体的,曲线与坐标轴之间的面积应当越大。
最理想的系统, 其包含的面积应当是1,而所有系统的包含的面积都应当大于0。这就是用以评价信息检索系统的最常用性能指标,平均准确率mAP其规范的定义如下:(其中P,R分别为准确率与召回率)

























 1666
1666

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








