mesh分割算法（自己学习过程中记录，不全）

注：总结肯定是不全的，当时是在学习过程中找和自己研究课题有正相关的才记录下来，其他可能好用的方法，但是对我近期做的事情不相关，在有限的时间内就没有做详细的记录。

一、迭代聚类：（基本和点云一致）

通常根据某种相似性度量标准，计算每个面或者顶点到簇质心的距离，将这些面或者顶点指定给相应集合，进行初始分类，然后后更新聚类初始状态，不断迭代。

可能适用的是：

变分形状逼近VSA(variational shape approximation)是一种基于k-means的迭代聚类算法。

《Variational shape approximation》 ，2004，ACM

（1.1）这篇文章就有一种曲面距离的度量标准。

（1.2）VSA算法还可以适用于网格简化，（根据重新排布法原理，可以一定程度上减少面片内部顶点，保留面片边界处顶点，从而实现网格简化操作。）

分割时的不足：VSA算法可能陷入局部最小和无限循环的问题中。
VSA效果：

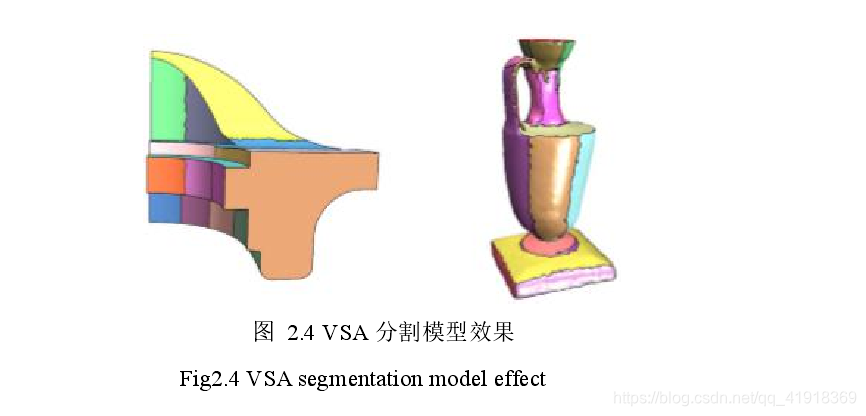
二、基于特征曲线的网格分割算法：

优先找到能够代表三维模型真实屋里结构的曲线，然后根据曲线进行分割。（关键就是利用曲率，将曲率大于设定阈值的点作为模型特征点，将特征点连接形成模型特征线，最后按照特征线进行分割）

三、区域增长算法：（和超体素的那个思路差不多）

基于区域生长的网络分割算法是一种局部贪婪算法，通过先依据某种集合信号量选定种子点，由种子点出发，向外生长延伸，不断并入相邻三角形，直至遇到模型边界停止生长，由此划分得到网格分割结果。

（利用的核心特征还是曲率和凹凸性）

四、基于动态网格分割：（暂不参考）

五、基于神经网络的mesh分割：（暂不参考）

MV-RNN，mesh-cnn
可参考链接：
https://blog.csdn.net/qq_41918369/article/details/108803156?spm=1001.2014.3001.5501