求一阶微分方程通解和特解

注：±C也可看作新的C

一、把y'换成dy/dx，dy与y放等式左边，dx与x放等式右边，对两边同时求不定积分。对于求特解的，还要把给出的点带入到结果中求出C。有时，题干不会明着告诉你要求特解，要自己判断能不能确定某一点点值，例：

求f(x)，题目本身不难，两边同时求导，得到y=C*e^(2x)，但是有原式可知，x=0时，等式右边的积分等于0，f(0)=ln2，所以C=ln2，得到特解

 

二、无法完全分离x和y时，把dy/dx放一边，其余的放另一边，然后判断式子属于一下何种情况，求解

1.

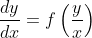
设u=y/x，原式y/x变为u，dy/dx中的y替换为ux，变为u+x*(du/dx)

2.一阶线性微分方程

结果直接为下式

 

式子中只留下一个C，在幂上的积分结果不用加C

3.

 

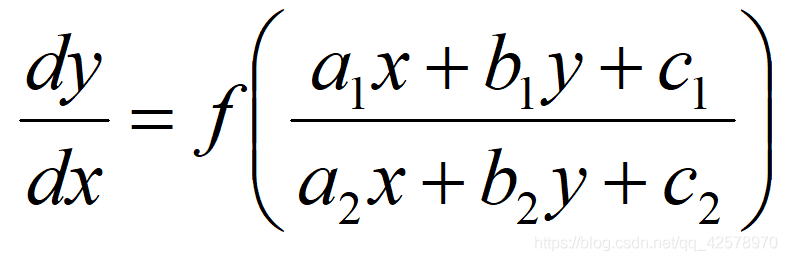
如果a1/a2=b1/b2=k，u=a2x+b2y，此时，a1x+b1y+c1变为ku+c1，a2x+b2y+c2变为u+c2

如果不相等，则由下式求出h，k

然后设x=X+h，y=Y+k，此时a1x+b1y+c1变为a1X+b1Y，a2x+b2y+c2变为a2X+b2Y。此时，分子分母依然有X和Y，可以上下同时除以X，然后用第一种方法求解

4.

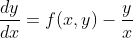
设u=xy，y变为u/x，dy/dx变为(du/dx-u/x)/x

5.伯努利方程

设u=y^(1-n)，转化为求

然后用情况2的解法求

6.

 

求对y的偏导时，直接把其余的一切未知数当成常数，对于求对x的偏导同理

通解如下式，选择一个即可。且通解中的x0，y0任取，一般取0，如果会出现广义积分（即反常积分）则取1

7

等式右边出现x，y的混合部分或多次重复出现的式子，令u=该式子

最后，如果上面任何一种情况都不符合，那就用X替换y，Y替换x，求出结果后代换回去