前言
在计算如下两个幂级数展开式时,在收敛域端点处的敛散性存在一些疑问,答案中提示用比值审敛法来判断,经过尝试,无法判断。因此查阅了一些相关资料,了解了双阶乘与阶乘的一些性质,学习了Wallis公式与Stirling公式的应用,计算出这两个幂级数展开式在收敛域端点是收敛的。
(1)
f
(
x
)
=
a
r
c
s
i
n
x
f(x)=arcsinx
f(x)=arcsinx 展开成x的幂级数
(2)
f
(
x
)
=
l
n
(
x
+
(
1
+
x
2
)
f(x)=ln(x+\sqrt{(1+x^2})
f(x)=ln(x+(1+x2) 展开成x的幂级数
由于(2)的x的幂级数展开式的绝对值就是(1)的x的幂级数展开式,证明(1)在收敛域内收敛,可以推出(2)在收敛域内绝对收敛,所以本文只需对(1)进行计算。
幂级数展开的基本步骤
- 对于 f ( x ) = a r c s i n x f(x)=arcsinx f(x)=arcsinx无法通过拆项或者配凑出常见的8个麦克劳林级数,因为幂级数展开式逐项可积可导的性质,考虑到先求导较为简单,采用先导后积的方法计算,此过程较为常规。
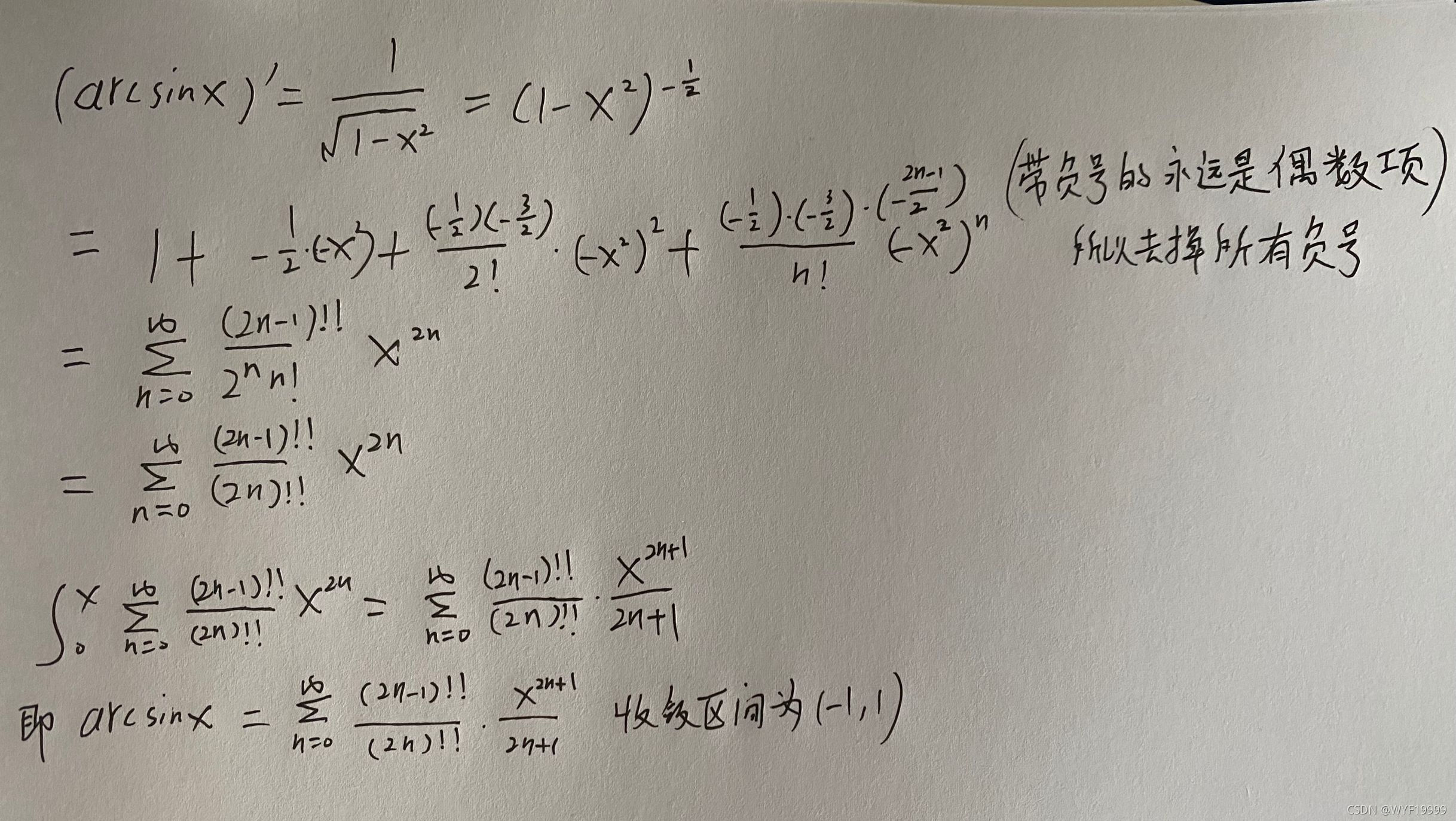
- 根据答案提示使用比值审敛法计算比值为1,并不能判断1和-1处的敛散性。
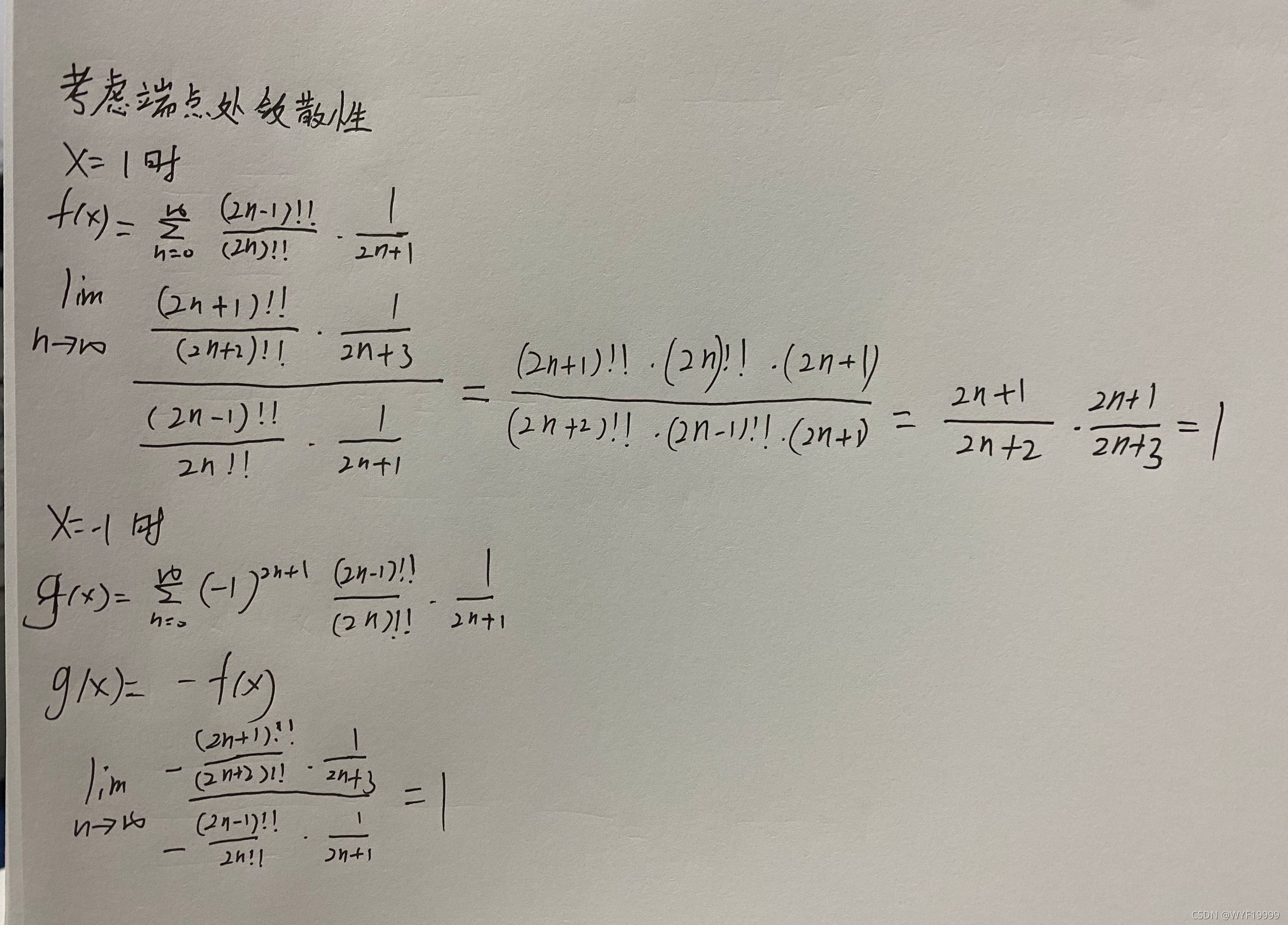
双阶乘与阶乘的互相转化
因为比值审敛法法无法判断端点处敛散性,所以尝试往P级数上靠。了解到可以用Stirling公式来拟合n!,为了使用Stirling公式,需要将双阶乘与阶乘进行转化,公式如下:
(
2
n
)
!
!
=
∏
k
=
1
n
(
2
k
)
=
2
n
n
!
(1)
(2n)!!=\prod_{k=1}^n(2k)=2^nn! \tag1
(2n)!!=k=1∏n(2k)=2nn!(1)
(
2
n
−
1
)
!
!
=
(
2
n
)
!
(
2
n
)
!
!
=
(
2
n
)
!
(
2
n
n
!
)
(2)
(2n-1)!!=\frac{(2n)!}{(2n)!!}=\frac{(2n)!}{(2^nn!)}\tag2
(2n−1)!!=(2n)!!(2n)!=(2nn!)(2n)!(2)
(1)可以理解为,偶数2n的双阶乘中,每个数都是偶数,所以将每个数都缩小一半,形成了n!再将缩小的
1
2
\frac{1}{2}
21还上,形成了
2
n
2^n
2n
(2)可以理解为,奇数的双阶乘中,每个数都是奇数,在(2n)!中,去除了所有偶数,剩下的就是(2n-1)!!
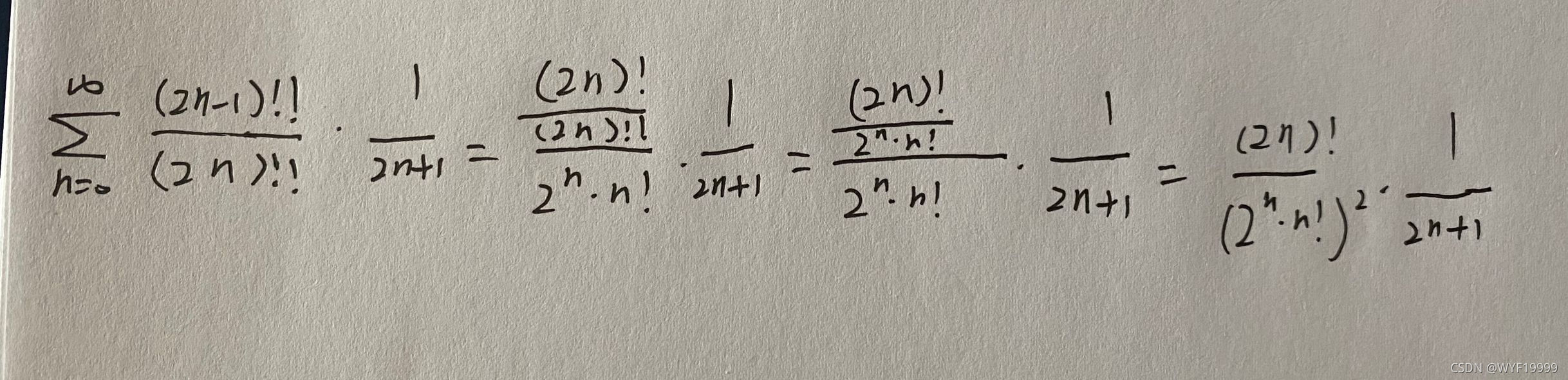
斯特林公式(Stirling’s approximation)
n的阶乘在n趋向正无穷时,可以用斯特林公式来进行等价,可以将n!与n的幂函数建立联系,公式为:
lim
n
→
∞
n
!
=
2
π
n
(
n
e
)
n
\lim_{n \to \infty} n!=\sqrt{2\pi n}(\frac{n}{e})^n
n→∞limn!=2πn(en)n
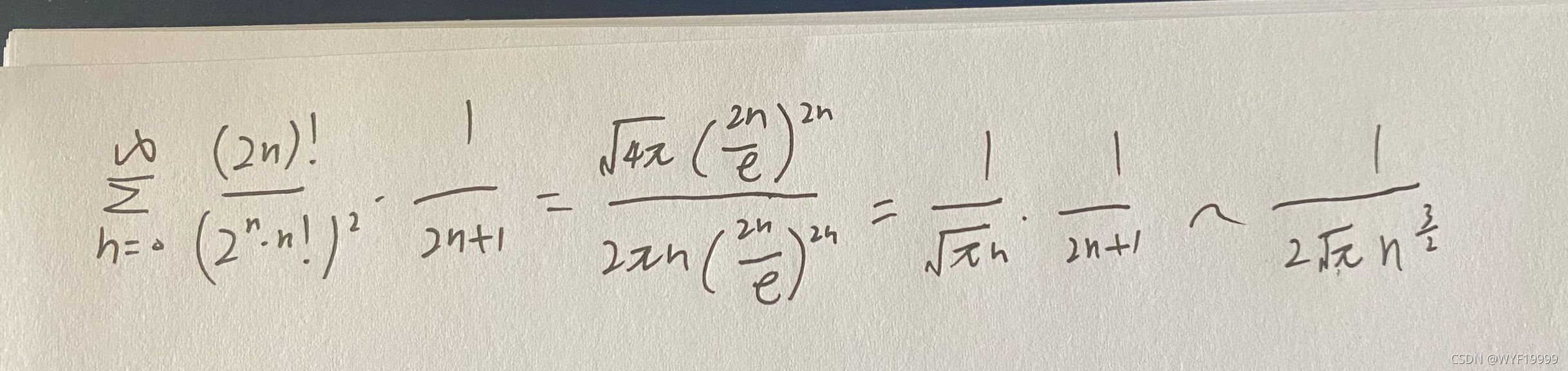
与p级数比较, 3 2 \frac{3}{2} 23>1,所以该级数在x=1处收敛,同理在x=-1处绝对收敛。
Wallis公式的推论
由双阶乘的比值,联想到直接Wallis公式的推论,而不需要进行双阶乘与阶乘的转化。
lim
n
→
∞
(
2
n
+
1
)
!
!
2
n
!
!
=
2
π
n
(1)
\lim_{n \to \infty} \frac{(2n+1)!!}{2n!!}= {\frac{2}{\sqrt{\pi}}}\sqrt{n} \tag1
n→∞lim2n!!(2n+1)!!=π2n(1)
lim
n
→
∞
(
2
n
)
!
!
(
2
n
−
1
)
!
!
=
n
π
(2)
\lim_{n \to \infty} \frac{(2n)!!}{(2n-1)!!}= {\sqrt{n\pi}}\tag2
n→∞lim(2n−1)!!(2n)!!=nπ(2)

结果与使用Stirling公式完全一样。
总结
通过两种方法的验证,最后得出结论:
a
r
c
s
i
n
x
=
∑
n
=
0
∞
(
2
n
−
1
)
!
!
(
2
n
)
!
!
(
2
n
+
1
)
x
∈
[
−
1
,
1
]
arcsinx=\sum_{n=0}^\infty\frac{(2n-1)!!}{(2n)!!(2n+1)} \quad x\in[-1,1]
arcsinx=n=0∑∞(2n)!!(2n+1)(2n−1)!!x∈[−1,1]
第一次使用LaTeX打数学公式,最后放一下Cmd Markdown公式指导手册,方便以后查阅。
https://www.zybuluo.com/codeep/note/163962#3%E5%A6%82%E4%BD%95%E8%BE%93%E5%85%A5%E6%8B%AC%E5%8F%B7%E5%92%8C%E5%88%86%E9%9A%94%E7%AC%A6








 本文探讨了在计算arcsinx和ln(x+(1+x^2))的幂级数展开时,如何利用Stirling公式与Wallis公式判断在收敛域端点的敛散性。通过转化双阶乘与阶乘的关系,以及与p级数的比较,证明了这两个幂级数在x=1和x=-1处的收敛性。总结了幂级数展开的方法和验证过程。
本文探讨了在计算arcsinx和ln(x+(1+x^2))的幂级数展开时,如何利用Stirling公式与Wallis公式判断在收敛域端点的敛散性。通过转化双阶乘与阶乘的关系,以及与p级数的比较,证明了这两个幂级数在x=1和x=-1处的收敛性。总结了幂级数展开的方法和验证过程。

















 4566
4566

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










