一.幂级数

1.幂级数的收敛区间
显然幂级数(2)在 x = 0 x=0 x=0处总是收敛的
(1)阿贝尔定理:
定理14.1:若幂级数(2)在 x = x ˉ ≠ 0 x=\bar x≠0 x=xˉ=0处收敛,则对满足不等式 ∣ x ∣ < ∣ x ˉ ∣ |x|<|\bar x| ∣x∣<∣xˉ∣的任何 x x x,幂级数(2)都绝对收敛;若幂级数(2)在 x = x ˉ x=\bar x x=xˉ处发散,则对满足不等式 ∣ x ∣ > ∣ x ˉ ∣ |x|>|\bar x| ∣x∣>∣xˉ∣的任何 x x x,幂级数(2)都发散
(2)幂级数的收敛半径与收敛区间:

(3)确定收敛半径:
定理14.2:对于幂级数(2),若 lim n → ∞ ∣ a n ∣ n = ρ \displaystyle\lim_{n\to\infty}\sqrt[n]{|a_n|}=ρ n→∞limn∣an∣=ρ则当
① 0 < ρ < + ∞ 0<ρ<+\infty 0<ρ<+∞时,幂级数(2)的收敛半径 R = 1 ρ R=\frac{1}{ρ} R=ρ1
② ρ = 0 ρ=0 ρ=0时,幂级数(2)的收敛半径 R = + ∞ R=+\infty R=+∞
③ ρ = + ∞ ρ=+\infty ρ=+∞,幂级数(2)的收敛半径 R = 0 R=0 R=0
定理14.3(柯西-阿达马定理;Cauchy-Hadamard Theorem):对于幂级数(2),若 lim n → ∞ ‾ ∣ a n ∣ n = ρ \overline{\displaystyle\lim_{n\to\infty}}\sqrt[n]{|a_n|}=ρ n→∞limn∣an∣=ρ则当
① 0 < ρ < + ∞ 0<ρ<+\infty 0<ρ<+∞时,幂级数(2)的收敛半径 R = 1 ρ R=\frac{1}{ρ} R=ρ1
② ρ = 0 ρ=0 ρ=0时,幂级数(2)的收敛半径 R = + ∞ R=+\infty R=+∞
③ ρ = + ∞ ρ=+\infty ρ=+∞,幂级数(2)的收敛半径 R = 0 R=0 R=0
(4)幂级数的一致收敛性:
定理14.4:若幂级数(2)的收敛半径为 R > 0 R>0 R>0,则幂级数(2)在其收敛区间 ( − R , R ) (-R,R) (−R,R)内的任一闭区间[a,b]上都一致收敛
定理14.5:若幂级数(2)的收敛半径为 R > 0 R>0 R>0,且在 x = R x=R x=R(或 x = − R x=-R x=−R)时收敛,则级数(2)在 [ 0 , R ] [0,R] [0,R](或 [ − R , 0 ] [-R,0] [−R,0])上一致收敛
2.幂级数的性质
(1)和函数的性质:
定理14.6:①幂级数(2)的和函数是(-R,R)上的连续函数
②若幂级数(2)在收敛区间的左(右)端点上收敛,则其则其和函数也在该端点上右(左)连续
(2)幂级数求导/求积后的收敛区间:

定理14.7:幂级数(2)与幂级数(7)(8)具有相同的收敛区间
(3)和函数求导/求积:
定理14.8:设幂级数(2)在收敛区间(-R,R)上的和函数为 f f f,若x为(-R,R)上任意1点,则
( i ) f (i)\,f (i)f在点x可导,且 f ′ ( x ) = ∑ n = 1 ∞ n a n x n − 1 f'(x)=\displaystyle\sum_{n=1}^{\infty}na_nx^{n-1} f′(x)=n=1∑∞nanxn−1
( i i ) f (ii)\,f (ii)f在[0,x]上可积,且 ∫ 0 x f ( t ) d t = ∑ n = 0 ∞ a n n + 1 x n + 1 \int_0^xf(t)dt=\displaystyle\sum_{n=0}^{\infty}\frac{a_n}{n+1}x^{n+1} ∫0xf(t)dt=n=0∑∞n+1anxn+1
该定理指出幂级数在收敛区间内可逐项求导和逐项求积
推论1:设 f f f为幂级数(2)在收敛区间(-R,R)上的和函数,则在(-R,R)上 f f f具有任何阶导数,且可逐项求导任何次,即 f ′ ( x ) = a 1 + 2 a 2 x + 3 a 3 x 2 + . . . + n a n x n − 1 + . . . f ′ ′ ( x ) = 2 a 2 + 3 ⋅ 2 a 3 x + . . . + n ( n − 1 ) a n x n − 2 + . . . . . . . . . . . . f ( n ) ( x ) = n ! a n + ( n + 1 ) n ( n − 1 ) . . . 2 a n + 1 x + . . . . . . . . . . . . f'(x)=a_1+2a_2x+3a_3x^2+...+na_nx^{n-1}+...\\f''(x)=2a_2+3·2a_3x+...+n(n-1)a_nx^{n-2}+...\\.........\\f^{(n)}(x)=n!a_n+(n+1)n(n-1)...2a_{n+1}x+...\\......... f′(x)=a1+2a2x+3a3x2+...+nanxn−1+...f′′(x)=2a2+3⋅2a3x+...+n(n−1)anxn−2+............f(n)(x)=n!an+(n+1)n(n−1)...2an+1x+............
推论2:记 f f f为幂级数(2)在点 x = 0 x=0 x=0某邻域上的和函数,则幂级数(2)的系数与 f f f在 x = 0 x=0 x=0处的各阶导数有如下关系: a 0 = f ( 0 ) , a n = f ( n ) ( 0 ) n ! ( n = 1 , 2... ) a_0=f(0),a_n=\frac{f^{(n)}(0)}{n!}\,(n=1,2...) a0=f(0),an=n!f(n)(0)(n=1,2...)
该推论还表明:若幂级数(2)在(-R,R)上有和函数 f f f,则幂级数(2)由 f f f在点 x = 0 x=0 x=0处的各阶导数所唯一确定
3.幂级数的运算
(1)幂级数相等:

定理14.9:若幂级数(2)与(9)在点x=0的某邻域内相等,则它们同次幂项的系数相等,即 a n = b n ( n = 0 , 1 , 2... ) a_n=b_n\,(n=0,1,2...) an=bn(n=0,1,2...)
由该定理还可推得:若幂级数(2)的和函数为奇(偶)函数则(2)式不出现偶(奇)次幂项
(2)幂级数的运算:
定理14.10:若幂级数(2),(9)的收敛半径分别为 R a , R b R_a,R_b Ra,Rb,则有 λ ∑ n = 0 ∞ a n x n = ∑ n = 0 ∞ λ a n x n ( ∣ x ∣ < R a ) ∑ n = 0 ∞ a n x n ± ∑ n = 0 ∞ b n x n = ∑ n = 0 ∞ ( a n ± b n ) x n ( ∣ x ∣ < R ) ( ∑ n = 0 ∞ b n x n ) ( ∑ n = 0 ∞ a n x n ) = ∑ n = 0 ∞ c n x n ( ∣ x ∣ < R ) λ\displaystyle\sum_{n=0}^{\infty}a_nx^n=\displaystyle\sum_{n=0}^{\infty}λa_nx^n\,(|x|<R_a)\\\displaystyle\sum_{n=0}^{\infty}a_nx^n±\displaystyle\sum_{n=0}^{\infty}b_nx^n=\displaystyle\sum_{n=0}^{\infty}(a_n±b_n)x^n\,(|x|<R)\\(\displaystyle\sum_{n=0}^{\infty}b_nx^n)(\displaystyle\sum_{n=0}^{\infty}a_nx^n)=\displaystyle\sum_{n=0}^{\infty}c_nx^n\,(|x|<R) λn=0∑∞anxn=n=0∑∞λanxn(∣x∣<Ra)n=0∑∞anxn±n=0∑∞bnxn=n=0∑∞(an±bn)xn(∣x∣<R)(n=0∑∞bnxn)(n=0∑∞anxn)=n=0∑∞cnxn(∣x∣<R)
其中 λ λ λ为常数, R = m i n { R a , R b } , c n = ∑ k = 0 n a k b n − k R=min\{R_a,R_b\},c_n=\displaystyle\sum_{k=0}^na_kb_{n-k} R=min{Ra,Rb},cn=k=0∑nakbn−k
二.函数的幂级数展开
1.泰勒级数
(1)概念:
(2)泰勒级数收敛于自身的条件:
定理14.11:设 f f f在点 x 0 x_0 x0具有任意阶导数,则 f f f在 ( x 0 − r , x 0 + r ) (x_0-r,x_0+r) (x0−r,x0+r)上等于其泰勒级数的和函数的充要条件是:对满足 ∣ x − x 0 ∣ < r |x-x_0|<r ∣x−x0∣<r的 ∀ x ∀x ∀x,有 lim n → ∞ R n ( x ) = 0 \displaystyle\lim_{n\to\infty}R_n(x)=0 n→∞limRn(x)=0这里 R n ( x ) R_n(x) Rn(x)是 f f f在 x 0 x_0 x0处的泰勒公式余项
(3)泰勒展开式:


(4)麦克劳林级数与各个形式的余项:

2.初等函数的幂级数展开式
求幂级数展开式的方法:①通过定义和定理14.11求得 ②从已知展开式出发,通过变量代换/四则运算/逐项求导/逐项求积求得
另外,某些非初等函数也可用幂级数的形式来表示,如 F ( x ) = ∫ 0 x e − t 2 d t = x − 1 1 ! x 3 3 + 1 2 ! x 5 5 − 1 3 ! x 7 7 + . . . + ( − 1 ) n n ! x 2 n + 1 2 n + 1 + . . . ( − ∞ < x < + ∞ ) F(x)=\int_0^xe^{-t^2}dt=x-\frac{1}{1!}\frac{x^3}{3}+\frac{1}{2!}\frac{x^5}{5}-\frac{1}{3!}\frac{x^7}{7}+...+\frac{(-1)^n}{n!}\frac{x^{2n+1}}{2n+1}+...\,(-\infty<x<+\infty) F(x)=∫0xe−t2dt=x−1!13x3+2!15x5−3!17x7+...+n!(−1)n2n+1x2n+1+...(−∞<x<+∞)
(1)多项式函数:


(2)指数函数:

(3)三角函数:

(4)对数函数:



(5)二项式函数:





(6)计算近似值:


三.复变量的指数函数与欧拉公式
1.复数项级数:

2.复数项幂级数:

3.复变量的指数函数:


4.欧拉公式:












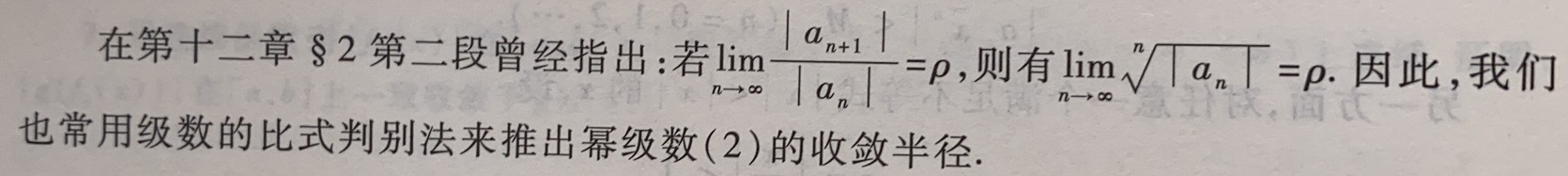




















 1170
1170











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








