自控原理学习笔记---控制系统稳定性分析

自控原理学习笔记
自控原理学习笔记专栏
第一章——反馈控制系统的动态模型
第二章——控制系统稳定性分析
第三章——连续时间系统性能分析
第四章——自动控制系统校正与综合
第五章——线性离散系统

---

系统稳定性分析

---

1.输入输出稳定-对于CLTIS

返回目录

1.1两种稳定状态

1.1.1 BIBO稳定

1. 定义：如果一个系统在一个有界输入或扰动作用下其响应是有限的。

2. 充要条件：
   $$y(t)={\int }_0^{t}g(\tau )u(t-\tau )d\tau \Rightarrow |y(t)|\le {\int }_0^t|g(\tau )|\cdot |u(t-\tau )|d\tau \le M{\int }_0^t|g(\tau )|d\tau$$
   若要使y（t）有界，则充要条件为$|g(\tau )|$绝对可积

   不可积例子：$g(t)=\frac{1}{t-1}$

3. 对于CLTIS，满足BIBO则只有左半平面极点：

   假设传递函数是冲激响应的Laplace变换，于是：
   $$\begin{gathered} G(s)={\int }_0^{\infty }g(t)e^{-st}dt\Rightarrow |G(s)|\le {\int }_0^{\infty }|g(t)|\cdot |e^{-st}|dt={\int }_0^{\infty }|g(t)|\cdot |e^{-\sigma t}|dt \\ ⟹if\sigma \ge 0,|G(s)|{|}_{s=\sigma +iw}\to \infty \le {\int }_0^{\infty }|g(t)|\cdot |e^{-\sigma t}|dt\le {\int }_0^{\infty }|g(t)|dt \end{gathered}$$

​ $|g(t)|$无界，与BIBO稳定矛盾，所有只有当$\sigma <0$，满足条件。

1.1.2 零输入稳定（渐近稳定）

1. 定义：当t趋近于无穷，由初始条件产生的响应趋于0。
2. 稳定充分必要条件：
   • 对于$\forall s_i,Re(s_i)<0时，CLTIS渐近稳定$
   • $Re(s_i)>0||\text{有重虚根}，CLTIS不稳定$
   • 仅存在单重虚根，其他$Re(s_j)<0$,LTIS临界定界。
3. 相关例子：

1.1.3 稳定性相关说明

• 对于LTIS，BIBO、零输入稳定都要求特征值均位于复平面左边
• 对于LTIS，稳定性只取决于系统固有性质（特征值），与外界条件无关。
• 稳定性具有一个局部特性（多个稳定点），但只在时变系统和非线性系统体现，时不变系统是全局的。

2. Routh-Hurwitz判据

返回目录

2.1 CLTIS稳定的必要条件

系统特征方程所有系数大于0

2.2 Routh判据

1. 列些Routh表

$$\begin{array}{l}{s}^n{a}_n{a}_{n-2}{a}_{n-4}\dots \\ s^{n-1}{a}_{n-1}{a}_{n-3}{a}_{n-5}\dots \\ s^{n-2}{b}_1{b}_2{b}_3\cdots \\ s^{n-3}{c}_1{c}_2\dots \\ \dots \\ s^0{h}_1\end{array}$$

2. 常规计算
   $$\begin{gathered} b_1=-\frac{\left[\begin{array}{cc}{a}_n& a_{n-2}\\ a_{n-1}& a_{n-3}\end{array}\right]}{a_{n-1}}{b}_2=-\frac{\left[\begin{array}{cc}{a}_n& a_{n-4}\\ a_{n-1}& a_{n-5}\end{array}\right]}{a_{n-1}} \\ {c}_1=-\frac{\left[\begin{array}{cc}{a}_{n-1}& a_{n-3}\\ b_1& b_2\end{array}\right]}{b_1}{c}_2=-\frac{\left[\begin{array}{cc}{a}_{n-1}& a_{n-5}\\ b_1& b_3\end{array}\right]}{b_1} \end{gathered}$$

3.判断稳定方法：

​ 第一列系数符号改变次数，就是特征根位于右半s平面的个数

​ 稳定充要条件：表中第一列系数全大于0

4. 举例：

   假设系统特征方程如下，用Routh判据判别系统稳定性
   $$s^4+2s^3+3s^2+4s+5=0$$
   解：
   $$\begin{array}{cccc}{s}^4& 1& 3& 5\\ s^3& 2& 4& 0\\ s^2& \frac{2\times 3-1\times 4}{2}=1& 5& 0\\ s^1& \frac{1\times 4-2\times 5}{1}=-6& 0& \\ s^0& 5& & \end{array}$$

显然第一列符号变化了两次，即在右平面极点数目为2，不稳定

2.3 相关应用

（1）首列系数为0

• 利用小$ϵ$法代替零值项，按常规方法继续求解。

• 若第一列全为正数，系统也不是渐近稳定，而是存在纯虚根，临界稳定

（2）某行系数全为0

表明s平面有对称于原点的实根，或共轭虚根 ，

• 取全为0的前一行，以其系数为辅助方程（只取偶次，只存在奇次行）

• 对辅助方程求导，系数代替全为0行

• 继续常规步骤

• 解辅助方程得到对称根

  举例说明：
  $$\begin{array}{lc}{s}^6+2s^5+6s^4+8s^3+10s^2+4s+4=0& \\ s^{6}166104& \\ s^{5}284& \\ s^{4}284& F(s)=2s^4+8s^2+4s^0\\ s^{3}00& F^{\prime }(s)=8s^3+16s\\ s^{3}816& \\ s^{2}44& \\ s^{1}8& \\ s^{0}4& \end{array}$$

（3）相关稳定性问题

利用换元的思想。

如求实部均小于2，则设u=s+2代入方程，将u当作方程变量，进行求解。

2.4 Hurwitz判据

将特征方程系数按如下形式列出。
$${\Delta }_n=\left|\begin{array}{cccccc}{a}_{n-1}& a_{n-3}& a_{n-5}& \cdots & \cdots & 0\\ a_n& a_{n-2}& a_{n-4}& \cdots & \cdots & ⋮\\ 0& a_{n-1}& a_{n-3}& \cdots & \cdots & ⋮\\ 0& a_n& a_{n-2}& \cdots & \cdots & ⋮\\ \cdots & \cdots & \cdots & \cdots & \dots & ⋮\\ \cdots & \cdots & \cdots & \cdots & a_1& 0\\ \cdots & \cdots & \cdots & \cdots & a_2& a_0\end{array}\right|$$

系统稳定的条件是系统行列式各阶主子式大于0
$${\Delta }_1=a_{n-1}>0,{\Delta }_2=\left|\begin{array}{cc}{a}_{n-1}& a_{n-3}\\ a_n& a_{n-2}\end{array}\right|>0,{\Delta }_3=\left|\begin{array}{ccc}{a}_{n-1}& a_{n-3}& a_{n-5}\\ a_n& a_{n-2}& a_{n-4}\\ 0& a_{n-1}& a_{n-3}\end{array}\right|>0,\cdots ,{\Delta }_n>0$$

3. 环路分析

返回目录

3.1环路分析基本思想

1. 不同频率正弦信号在线性系统中的传输，输出被放大、缩小还是自持振荡完全取决于频率特性。

2. 记（-1，i0）为临界点。相角交越频率为当相角为-180°时的频率，此时若幅值为1则为自激条件。

3. 简化Nyquist判据：

   如果$|L(i{w}_{pc})>1|$，环路上$w_{pc}$信号被放大，闭环系统不稳定。

   如过$|L(i{w}_{pc})<1|$，环路上$w_{pc}$信号被衰减，闭环系统稳定。

3.2 稳定程度的性能指标（相对稳定）

1. 增益裕度

   ​
   $$\begin{gathered} g_m=\frac{1}{|L(i{w}_{pc})|} \\ \text{要求:}{g}_m\ge 2 \end{gathered}$$
   

2. 相角裕度
   $$\begin{gathered} {\phi }_m=180°+\angle L(i{w}_c) \\ {\phi }_m=30°\sim 60° \end{gathered}$$

3. 模裕度(当有谐振需要考虑模裕度)
   $$s_m=\underset{w}{\min }|L(iw)+1|=\frac{1}{\underset{w}{\max }|S(iw)|}=\frac{1}{M_s}$$
   

3.3 环路整形

1. 对于开环稳定、闭环不稳定的系统，通过降低开环增益可以避开临界点，使系统闭环稳定
2. 通过控制器给系统引入开环零极点，改变频率特性的形状，绕开临界点。

4.Nyquist判据

返回目录

4.1 与幅角原理关系

4.2 补圆

4.3判别方法

设开环传递函数$L(s)$右半复平面的极点数为P，

1. Nyquist曲线顺时针围绕（-1，i0）圈数为$w_n$,则闭环系统在右半复平面的极点数为$N=w_n+P$

2. 闭环系统稳定的充要条件是N=0，即Nyquist曲线围绕（-1，i0）的逆时针圈数为P

3. 相关说明：L（s）若具有RHP极点，闭环系统稳定必要条件$|L(i{w}_{pc})|>1$，即必须要绕（-1，i0）。

4.4 相关例子

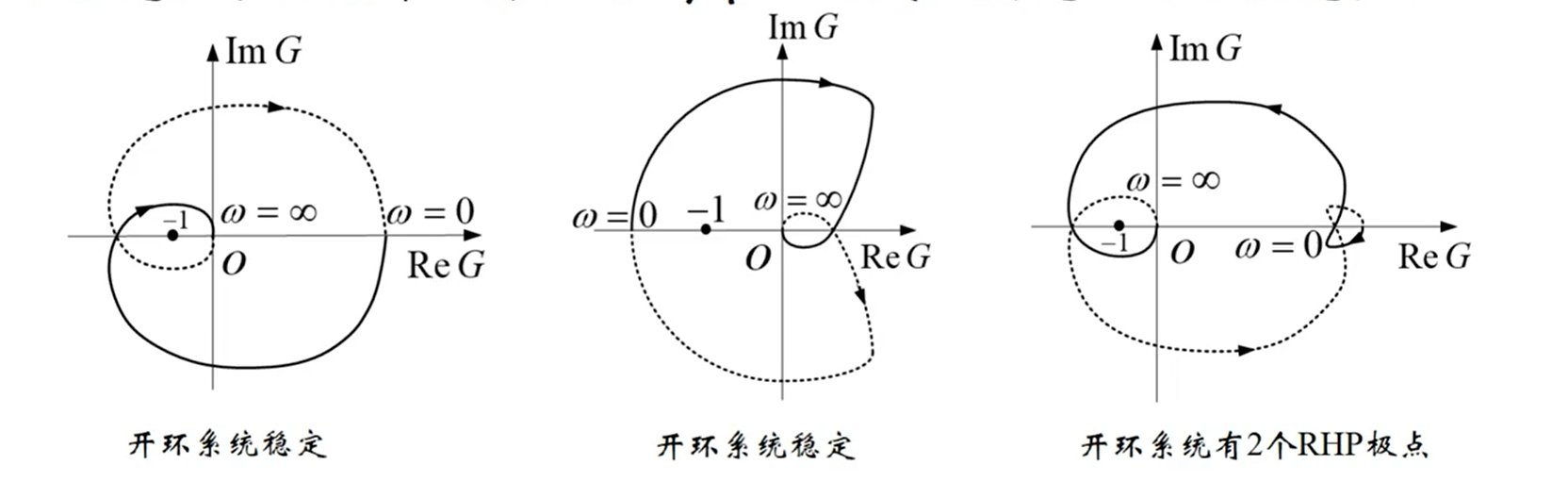
开环极点数	0	0	2
顺时针围绕圈数	1	1	-2
闭环极点	0稳定	0稳定	0稳定

2. n个积分环节补圆$N\pi$

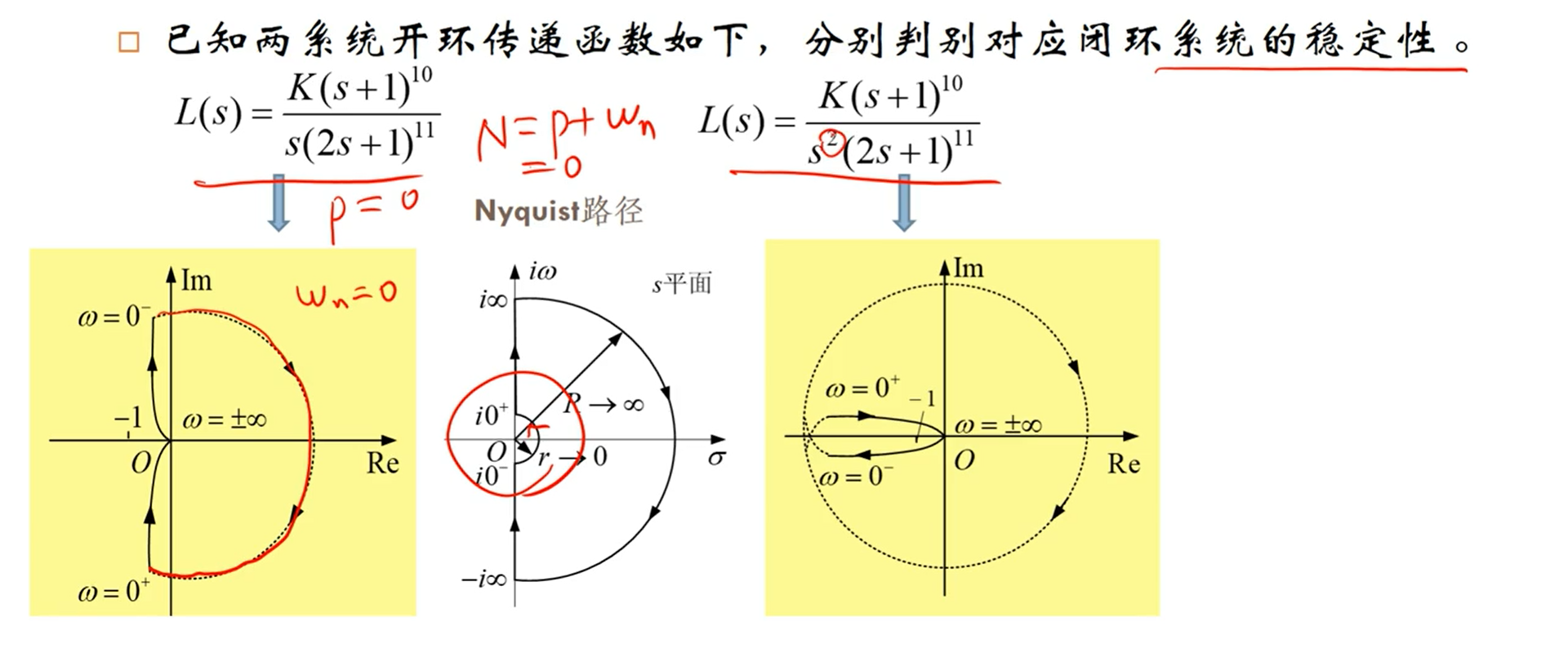
系统增加开环极点，即将系统相角变大，使之不用穿越至第二象限，从而达到使$w_n=0$.

5.非线性系统稳定性及自振分析

返回目录

5.1 用描述函数分析的条件

1. 非线性控制系统结构图一般能简化成如上图所示最简形式。
2. 非线性环节的输入输出特性是奇对称的，保证非线性在正弦作用下不含常值分量。
   3. 非线性系统具有良好的低通滤波特性。

5.2稳定性判据

1. 闭环系统近似频率特性

$$\Phi (iw)=\frac{N(A)G(iw)}{1+N(A)G(iw)}$$

2. 闭环系统的特征方程为：
   $$1+N(A)G(iw)=0⟹G(iw)=-\frac{1}{N(A)}$$

3. 判据：

   在复平面上分别画出$-\frac{1}{N(A)}$和$G(iw)$，根据两者包围情况可判别稳定性（类比Nyquist判据）————临界点-1变成了临界线$-\frac{1}{N(A)}$

   （1）若两条曲线没有交点，则非线性系统稳定

   （2）若存在交点，则非线性系统不稳定————由不稳定区域$G(iw)$包围区域进入稳定区域$-\frac{1}{N(A)}$的交点 为自振点，另外一个则为不稳定周期运动的点。

5.2 自振必要条件

负倒曲线$–\frac{1}{N(A)}$与$G(iw)$有交点。在交点处于临界稳定状态，满足$N(A)\ast G(iw)=-1$即：
$$\{\begin{array}{c}|N(A)|\cdot |G(iw)|=1\\ \angle N(A)+\angle G(iw)=-180°\end{array}$$

1. 自振参数计算

2.消除自振方法：

改变N(A)或G(s)的参数，使两者在s平面上无交点，且$-\frac{1}{N(A)}$不能被$G(iw)$包围.

6.Bode图稳定性分析

返回目录

6.1 与Nyquist对应关系

Nyquist图	Bode图
单位圆	幅相曲线0dB线
单位圆外部和内部	幅相曲线上侧和下侧
负实轴	相角为-180度曲线
$w_{pc}和w_c$对应关系如下	$w_{pc}和w_c$对应关系如下
积分环节nyquist补圆$\nu \pi$	相频曲线向上补$\nu \frac{\pi }{2}$
等幅振荡$\frac{1}{(s^2+w_n^2{)}^2}$,幅相半闭合曲线（Nyquist的一半）需要补$\nu \pi$从$w_n^{-}到w_n^{+}$	相频向下补$\nu \pi$

6.2 相频特性-穿越次数

限定：正负穿越讨论一定要在穿越频率以内

Bode图的相频曲线图从-180度以下穿越至-180度以上为正穿越，反之为负穿越。

Bode图若从-180度线往上出发，为半次正穿越,记$C^{+}=0.5$

6.3 计算相关裕度

相关裕度	求解公式
幅值裕度	$G_m=20\lg{g_m}=0-20\lg
相角裕度	${\phi }_m=180°+\angle L(i{w}_c)$
模裕度	$l_m=20\lg s_m=20\lg

7.计算稳定性步骤

返回目录

1. 计算$w_{pc}$：利用各个环节贡献相角量进行计算，避免使用将iw代入开环传递函数进行化简。
   $$\begin{gathered} 判定如下系统是否闭环稳定，已知单位负反馈系统的开环传递函数如下（所有的T_i>0），并给依据。 \\ L(s)=\frac{1}{\left(T_{1}s+1\right)\left(T_{2}s+1\right)\left(T_{3}s+1\right)\left(T_{4}s+1\right)\left(T_{5}s+1\right)\left(T_{6}s+1\right)} \end{gathered}$$

$$\begin{array}{c}解：\angle L\left(\text{ i }{p}_{pc}\right)=\arctan T_1{\omega }_{pc}-\arctan T_2{\omega }_{pc}\cdots \arctan T_6{\omega }_{pc}=-180\\ 令w_{pc}=w_x\\ L(i{w}_{pc})=\frac{1}{\sqrt{{\left(T_1{w}_x\right)}^2+1}\cdots \cdots \sqrt{{\left(T_6{w}_x\right)}^2+1}}\le 1\\ \text{ 只有当 }{\omega }_x=0|L(i{w}_{pc})|=1\\ \text{ 而L（s）起点为(1,i0)}L(s)\\ \text{所以系统没有围绕(-1,i0)，即系统没有RHP极点，闭环系统稳定}\end{array}$$