坐标变换的艺术—估计轴系的扩展反电势公式推导
Shigeo Morimoto将扩展反电势拓展至估计轴系,本文将对其进行公式演绎。
公式推导过程
坐标变换图示
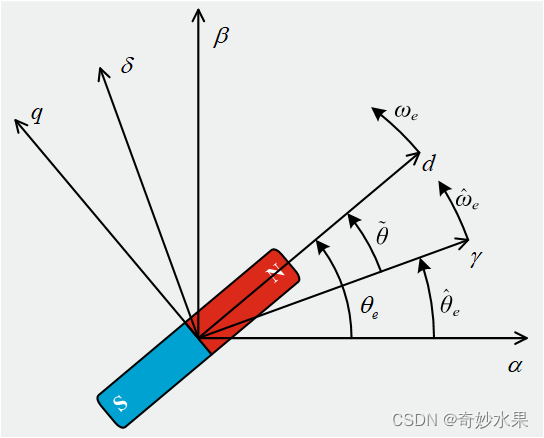
注:论文中的角度误差使用 θ e \theta_e θe表示,本文则使用 θ ~ \tilde{\theta} θ~表示
两相静止轴系,电机电压方程为
[ u α u β ] = [ R 0 0 R ] [ i α i β ] + d d t { [ L 0 − L 1 cos 2 θ e − L 1 sin 2 θ e − L 1 sin 2 θ e L 0 + L 1 cos 2 θ e ] [ i α i β ] } + ω e ψ f [ − sin θ e cos θ e ] \left[ \begin{array}{c} u_{\alpha}\\ u_{\beta}\\ \end{array} \right] =\left[ \begin{matrix} R& 0\\ 0& R\\ \end{matrix} \right] \left[ \begin{array}{c} i_{\alpha}\\ i_{\beta}\\ \end{array} \right] +\frac{\mathrm{d}}{\mathrm{dt}}\left\{ \left[ \begin{matrix} L_0-L_1\cos 2\theta _e& -L_1\sin 2\theta _e\\ -L_1\sin 2\theta _e& L_0+L_1\cos 2\theta _e\\ \end{matrix} \right] \left[ \begin{array}{c} i_{\alpha}\\ i_{\beta}\\ \end{array} \right] \right\} +\omega _e\psi _f\left[ \begin{array}{c} -\sin \theta _e\\ \cos \theta _e\\ \end{array} \right] [uαuβ]=[R00R][iαiβ]+dtd{
[L0−L1cos2θe−L1sin2θe−L1sin2θeL0+L1cos2θe][iαiβ]}+ωeψf[−sinθecosθe]
式中:
θ ~ = θ e − θ ^ , L 0 = L d + L q 2 , L 1 = L q − L d 2 \tilde{\theta}=\theta _e-\hat{\theta}\text{,}L_0=\frac{L_d+L_q}{2}\text{,} L_1=\frac{L_q-L_d}{2} θ~=θe−θ^,L0=2Ld+Lq,L1=2Lq−Ld
坐标变换矩阵满足
[ f α f β ] = [ cos θ e − sin θ e sin θ e cos θ e ] [ f d f q ] = T d q / α β [ f d f q ] [ f α f β ] = [ cos θ ^ − sin θ ^ sin θ ^ cos θ ^ ] [ f γ f δ ] = T γ δ / α β [ f γ f δ ] \left[ \begin{array}{c} f_{\alpha}\\ f_{\beta}\\ \end{array} \right] =\left[ \begin{matrix} \cos \theta _e& -\sin \theta _e\\ \sin \theta _e& \cos \theta _e\\ \end{matrix} \right] \left[ \begin{array}{c} f_d\\ f_q\\ \end{array} \right] =T_{dq/\alpha \beta}\left[ \begin{array}{c} f_d\\ f_q\\ \end{array} \right] \\ \left[ \begin{array}{c} f_{\alpha}\\ f_{\beta}\\ \end{array} \right] =\left[ \begin{matrix} \cos \hat{\theta}& -\sin \hat{\theta}\\ \sin \hat{\theta}& \cos \hat{\theta}\\ \end{matrix} \right] \left[ \begin{array}{c} f_{\gamma}\\ f_{\delta}\\ \end{array} \right] =T_{\gamma \delta /\alpha \beta}\left[ \begin{array}{c} f_{\gamma}\\ f_{\delta}\\ \end{array} \right] [fαfβ]=[cosθesinθe−sinθecosθe][fdfq]=Tdq/αβ[fdfq][fαfβ]=[cosθ^sinθ^−sinθ^cosθ^][fγfδ]=Tγδ/αβ[fγfδ]
同时,坐标变换矩阵是单位正交矩阵,可得
T − 1 = T − T T^{-1}=T^{-T} T−1=T−T
因此,电压方程可重写为
T γ δ / α β [ u γ u δ ] = [ R 0 0 R ] T γ δ / α β [ i γ i δ ] + d d t { [ L 0 − L 1 cos 2 θ e − L 1 sin 2 θ e − L 1 sin 2 θ e L 0 + L 1 cos 2 θ e ] T γ δ / α β [ i γ i δ ] } + ω e ψ f [ − sin θ e cos θ e ] T_{\gamma \delta /\alpha \beta}\left[ \begin{array}{c} u_{\gamma}\\ u_{\delta}\\ \end{array} \right] =\left[ \begin{matrix} R& 0\\ 0& R\\ \end{matrix} \right] T_{\gamma \delta /\alpha \beta}\left[ \begin{array}{c} i_{\gamma}\\ i_{\delta}\\ \end{array} \right] +\frac{\mathrm{d}}{\mathrm{dt}}\left\{ \left[ \begin{matrix} L_0-L_1\cos 2\theta _e& -L_1\sin 2\theta _e\\ -L_1\sin 2\theta _e& L_0+L_1\cos 2\theta _e\\ \end{matrix} \right] T_{\gamma \delta /\alpha \beta}\left[ \begin{array}{c} i_{\gamma}\\ i_{\delta}\\ \end{array} \right] \right\} +\omega _e\psi _f\left[ \begin{array}{c} -\sin \theta _e\\ \cos \theta _e\\ \end{array} \right] Tγδ/αβ[uγuδ]=[R00R]Tγδ/αβ[iγiδ]+dtd{
[L0−L1cos2θe−L1sin2θe−L1sin2θeL0+L1cos2θe]Tγδ/αβ[iγiδ]}+ωeψf[−sinθecosθe]
整理可得:
[ u γ u δ ] = T γ δ / α β − 1 [ R 0 0 R ] T γ δ / α β [ i γ i δ ] + T γ δ / α β − 1 d d t { [ L 0 − L 1 cos 2 θ e − L 1 sin 2 θ e − L 1 sin 2 θ e L 0 + L 1 cos 2 θ e ] T γ δ / α β [ i γ i δ ] } + T γ δ / α β − 1 ω e ψ f [ − sin θ e cos θ e ] \left[ \begin{array}{c} u_{\gamma}\\ u_{\delta}\\ \end{array} \right] =T_{\gamma \delta /\alpha \beta}^{-1}\left[ \begin{matrix} R& 0\\ 0& R\\ \end{matrix} \right] T_{\gamma \delta /\alpha \beta}\left[ \begin{array}{c} i_{\gamma}\\ i_{\delta}\\ \end{array} \right] +T_{\gamma \delta /\alpha \beta}^{-1}\frac{\mathrm{d}}{\mathrm{dt}}\left\{ \left[ \begin{matrix} L_0-L_1\cos 2\theta _e& -L_1\sin 2\theta _e\\ -L_1\sin 2\theta _e& L_0+L_1\cos 2\theta _e\\ \end{matrix} \right] T_{\gamma \delta /\alpha \beta}\left[ \begin{array}{c} i_{\gamma}\\ i_{\delta}\\ \end{array} \right] \right\} +T_{\gamma \delta /\alpha \beta}^{-1}\omega _e\psi _f\left[ \begin{array}{c} -\sin \theta _e\\ \cos \theta _e\\ \end{array} \right] [uγuδ]=Tγδ/αβ−1[R00R]Tγδ/αβ[iγiδ]+Tγδ/αβ−1dtd{
[L0−L1cos2θe−L1sin2θe−L1sin2θeL0+L1cos2θe]Tγδ/αβ[iγiδ]}+Tγδ/αβ−1ωeψf[−sinθecosθe]
对等式右边的式子逐一进行整理,第一项
T γ δ / α β − 1 [ R 0 0 R ] T γ δ / α β [ i γ i δ ] ⇒ [ cos θ ^ sin θ ^ − sin θ ^ cos θ ^ ] [ R 0 0 R ] [ cos θ ^ − sin θ ^ sin θ ^ cos θ ^ ] [ i γ i δ ] ⇒ [ R 0 0 R ] [ i γ i δ ] (记为 A [ i γ i δ ] ) \begin{aligned} &T_{\gamma \delta /\alpha \beta}^{-1}\left[ \begin{matrix} R& 0\\ 0& R\\ \end{matrix} \right] T_{\gamma \delta /\alpha \beta}\left[ \begin{array}{c} i_{\gamma}\\ i_{\delta}\\ \end{array} \right] \\ \Rightarrow& \left[ \begin{matrix} \cos \hat{\theta}& \sin \hat{\theta}\\ -\sin \hat{\theta}& \cos \hat{\theta}\\ \end{matrix} \right] \left[ \begin{matrix} R& 0\\ 0& R\\ \end{matrix} \right] \left[ \begin{matrix} \cos \hat{\theta}& -\sin \hat{\theta}\\ \sin \hat{\theta}& \cos \hat{\theta}\\ \end{matrix} \right] \left[ \begin{array}{c} i_{\gamma}\\ i_{\delta}\\ \end{array} \right] \\ \Rightarrow& \left[ \begin{matrix} R& 0\\ 0& R\\ \end{matrix} \right] \left[ \begin{array}{c} i_{\gamma}\\ i_{\delta}\\ \end{array} \right] \text{(记为}A\left[ \begin{array}{c} i_{\gamma}\\ i_{\delta}\\ \end{array} \right] \text{)} \end{aligned} ⇒⇒Tγδ/αβ−1[R00R]Tγδ/αβ[iγiδ][cosθ^−sinθ^sinθ^cosθ^][R00R][cosθ^sinθ^−sinθ^cosθ^][








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2628
2628

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








