2025年第十届“数维杯”大学生数学建模挑战赛【C】题论文+代码+结果

本文将对数维杯每个赛题进行初步赛题浅析-帮助大家尽快的完整选题，梳理每个题目的设计模型、难度、可能遇到的难点

赛题难度 A:B:C=5:4:3

预估选题人数A:B:C=1:2:3

下面我们将分别对A题、B题、C题进行问题简介、求解思路、所需模型以及可以改进的创新点进行详细描述。

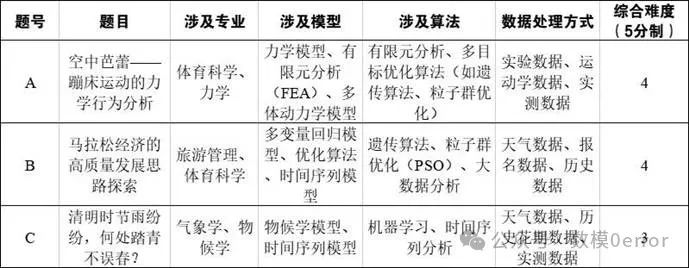
A题：空中芭蕾——蹦床运动的力学行为分析

问题简介

蹦床运动是利用蹦床的反弹性质在空中展示技能技巧的竞技运动。在运动过程中，运动员的起跳、腾空和下落等动作都会受到物理规律的影响。本问题旨在分析运动员在起跳瞬间的发力机制，运动员在空中飞行和落地过程中的受力情况，以及当多名运动员同时进行蹦床运动时蹦床的受力情况和疲劳损伤程度。

求解思路

• 起跳瞬间的发力机制分析

•步骤1：建模分析运动员的起跳瞬间发力方向和大小。

•步骤2：利用数值模拟方法验证模型的合理性。

• 运动员在空中的动力学分析

•步骤1：描述运动员在空中的重力和空气阻力的影响。

•步骤2：建立运动员在空中的动力学方程。

•步骤3：确定运动员落地时的速度和受力情况。

•步骤4：通过对不同起跳高度和落地姿势的优化，减少落地时的冲击力。

• 多名运动员同时进行蹦床运动的力学分析

•步骤1：多体动力学建模。

•步骤2：计算蹦床在多个运动员同时跳动时的受力情况。

•步骤 3：通过调整起跳时间和体重分布等因素，优化蹦床的受力情况和疲劳损伤程度。

具体而言：

所需模型

• 简化力学模型：考虑运动员为刚体模型，利用牛顿第二定律进行动力学分析。

• 有限元分析(FEA)：通过有限元方法模拟运动员起跳和蹦床压缩过程。

• 多体动力学模型：利用多体动力学软件（如   ADAMS、SIMULIA）模拟多名运动员同时跳动的力学过程。

进一步可以改进的创新点

• 引入生物力学因素：考虑运动员的具体生理特征和肌肉分布，优化模型的精细度。

• 动态模型扩展：建立考虑空气阻力变化和温度影响的动态模型。

• 机器学习算法：利用机器学习算法预测运动员的最佳起跳战术，提高竞技水平。

B题：马拉松经济的高质量发展思路探索

问题简介

马拉松赛事近年来数量快速增长，带来了显著的经济效益。本问题旨在通过数据分析和模型构建，科学筛选适宜举办马拉松赛事的城市和时间，优化路线设计以提升选手舒适度，推动马拉松赛事高质量发展。

求解思路

• 筛选适宜举办城市的窗口期和规模

•步骤1：综合考虑气象、城市承载能力、人口规模和报名热度等因素。

•步骤2：构建多变量回归模型，评估各地适宜举办马拉松的条件。

•步骤3：利用天气数据验证模型的有效性。

• 优化跑道路线设计

•步骤1：建立评价函数，考虑景点和住宿容量。

•步骤2：使用优化算法，设计最优跑步线路。

•步骤3：结合景点和餐饮设施，设计增益节点，优化跑步路线。

• 构建综合评估体系

•步骤1：考虑炎热天气的影响，优化路线。

•步骤2：通过多目标优化算法，平衡树荫覆盖率、交通影响和赛道坡度等因素。

所需模型

• 多变量回归模型：评估城市适宜举办马拉松的条件。

• 优化算法：如遗传算法、粒子群优化（PSO）等，优化路线设计。

• 多目标优化模型：平衡树荫覆盖率、交通影响和赛道坡度。

进一步可以改进的创新点

• 大数据分析：利用大数据技术分析历史数据，精准预测天气和人流。

• 人工智能技术：引入AI技术优化赛事组织和路线设计。

• 动态调整策略：根据实时天气数据，动态调整赛事时间、地点和路线。

C题：清明时节雨纷纷，何处踏青不误春？

问题简介

清明时节是春季的重要节气，人们多以踏青春游和扫墓祭奠的方式过节。本问题旨在通过气象学和物候学的视角，分析清明时节的天气规律，并建立花卉开放时间预测模型，为踏青赏花提供科学依据。

求解思路

• 分析“雨纷纷”的降雨量区间和持续时间

•步骤1：明确“雨纷纷”的物理标准。

•步骤2：建立降雨量和持续时间的数学模型。

•步骤3：利用近20年的天气数据，验证模型的有效性。

•步骤4：利用新实况数据修正模型。

• 建立花卉开放时间预测模型

•步骤1：结合物候学和气象学知识，建立花卉开放时间模型。

•步骤2：利用历史气象和花期数据训练模型。

•步骤3：预测2026年各花卉的开放时间。

•步骤4：设计赏花自由行攻略。

• 延长“赏花经济”产业链

•步骤1：通过延长花期，延长赏花经济产业链。

•步骤2：建立数学模型评估新措施的经济效益。

•步骤3：提出具体措施并给出经济效益预测。

所需模型

• 物候模型：结合气象数据预测各花卉开放时间。

• 时间序列模型：利用历史数据预测未来花卉开放时间。

• 经济效益模型：评估延长花期后的综合经济效益。

进一步可以改进的创新点

• 集成预测模型：结合多种预测方法（如机器学习、时间序列分析）提高预测准确性。

• 农业技术应用：利用现代农业技术（如智能温室、气候控制设施）延长花卉花期。

• 旅游经济模型：构建综合模型评估赏花经济对旅游行业的影响，优化城市旅游策略。

一、问题重述

1.1 问题背景

2025 年第十届数维杯大学生数学建模挑战赛 C 题，将我们带入“清明时节雨纷纷，何处踏青不误春”的诗意情境。清明节，这个处于每年 4 月 4 日至 6 日的特殊时段，宛如一座桥梁，连接着自然节气与传统节日。它不仅是大自然万物复苏、草木萌动、百花争艳的时节，南方呈现气清景明之态，北方也逐渐断雪，气温回升；更是中华民族千年文化传承的重要时刻，人们以踏青春游与扫墓祭奠，寄托情感，传承记忆，兼具自然与人文的双重魅力。

每至清明，冷空气势力渐弱，海洋暖湿空气则活跃北上，二者常在江南地区交汇，于是天空便飘起如丝如缕的绵绵细雨，“清明时节雨纷纷”这句千古名句也因此广为流传。然而，由于地形、大气环流、海陆位置等诸多因素的影响，不同地区的降雨情况可谓千差万别。

与此同时，杏花、油菜花、杜鹃花、樱花、牡丹等花卉，仿佛在进行一场盛大的接力赛，从南至北依次绽放，绘就春日里一道绝美的风景线。但花期就像一位调皮的精灵，极易受到气温、光照、降水等气象因子的摆弄，充满了不确定性，这也让渴望踏青赏花的人们满心期待又有些许担忧，究竟何时才能欣赏到最绚烂的花朵呢？

近年来，文旅产业如同一匹黑马，蓬勃发展，清明假期更是成为人们亲近自然、感受传统文化的黄金时段。如何精准把握清明时节的气象规律，深度挖掘其中蕴含的文旅价值，已然成为摆在我们面前亟待解决的重要课题。

1.2 数据来源

• 美国国家海洋和大气管理局(NOAA)下设的国家环境信息中心(NCEI)

  : 这里宛如一座气象数据的宝库，发布着自 1929 年至今的全球站点逐日气象数据集，网址为：https://www.ncei.noaa.gov/data/global-summary-of-the-day/archive/ 。通过它，我们能追溯历史气象的轨迹，探寻气候的变化规律。

• 天气网

  ：如同一位不知疲倦的气象记录员，从 1981 年起，为世界 241 个国家提供历史天气信息和最新天气预报。站点数据库的数据每三小时记录一次，每天八次，网址为：https://rp5.ru/ 。高频次的数据记录，为我们细致分析气象变化提供了有力支撑。

• 花期观测资料

  ：这些资料散落在学术论文和权威平台之中，如同等待我们发掘的宝藏。它们记录着花卉生长的秘密，是解开花期预测谜题的关键线索。

• 线上资料

  ：众多网址也为我们提供了丰富的信息，像 https://tianqi.2345.com/wea_history/57036.htm 等，它们如同一个个知识的小站，为我们的研究提供了多维度的参考。

1.3 注意事项

数据收集与分析，就如同大厦的基石，是建模分析的基础与关键。在撰写论文时，务必做到观点鲜明，如同旗帜般醒目；分析有据，每一个论点都有坚实的数据与理论支撑；结论明确，不含糊其辞。同时，若使用大型语言模型和人工智能工具，需在报告中坦诚相告，明确指出使用的模型以及目的，并且在建模论文之后附加 AI 使用情况报告，确保整个研究过程的透明与规范。

1.4 参考文献

一系列与气象预测、花期预测及相关经济分析等方面的参考文献，宛如一盏盏明灯，为我们的建模之路指引方向。它们或是前人在气象预测领域的智慧结晶，或是对花卉花期与气象因子关系的深入探究，又或是对赏花经济发展的思考，为我们提供了丰富的理论和方法参考。

1.5 赛题声明

本赛事所有赛题如同珍贵的宝藏，仅授权给 2025 年第十届数维杯数学建模挑战赛参赛队伍使用。任何未经组委会书面授权的组织及个人，严禁将其用于校内竞赛、篡改、复制等侵权行为，以维护赛事的公正性与权威性。

1.6 问题提出

• 问题 1

  ：我们需要依据天气现象分类标准，像侦探寻找线索一样，明确“雨纷纷”对应的降雨量区间及降雨持续时间范围。接着，运用天气学的基本知识，在合理简化的基础上，搭建数学模型，预测 2026 年清明假期西安、吐鲁番、婺源、杭州、毕节、武汉、洛阳等地是否会“雨纷纷”。同时，利用近 20 年的天气资料，复盘 2025 年清明的天气情况，以此验证模型的合理性。最后，还需给出利用最新天气实况修正模型的巧妙方法。

• 问题 2

  ：依据气象学或物候学的知识，为杏花、油菜花、杜鹃花、樱花、牡丹中的 2 - 3 种代表性花卉，打造专属的开放时间、花期等预报模型。这就像是为花卉生长装上一个精准的时钟，预判春花何时绽放，为人们的赏花之旅增添一道“科技保险”。

• 问题 3

  ：根据 2026 年清明假期天气预报和花期预测，精心为游客拟一份清明踏青赏花自由行攻略。这份攻略如同一位贴心的导游，帮助游客避开天气和花期的“小陷阱”，尽情享受美好的赏花时光。

• 问题 4

  ：撰写一份报告呈给地方政府，为延长“赏花经济”产业链出谋划策，让“赏花经济”拥有如同超长花期般的持久活力。并且建立数学模型，清晰地说明采取这些措施后，可能为地方带来的经济效益，为政府决策提供有力的科学依据。

二、问题分析

2.1 数据作用和意义

• 问题 1

  ：NOAA 和天气网的数据，犹如一座蕴藏丰富的矿山，包含日降水量、持续时长、相对湿度、850hPa 涡度场等核心变量。通过对近 20 年清明期间这些数据的“开采”与分析，我们能够像地质学家确定矿脉一样，明确“雨纷纷”对应的降雨量区间及降雨持续时间范围。例如，通过统计各地区清明期间的平均降水量和降雨持续时间，为“雨纷纷”制定一个科学合理的标准。同时，这些数据还是模型训练、验证与修正的“原材料”，经过精心“加工”，能大幅提高模型的准确性与可靠性。

• 问题 2

  ：除气象数据外，花期观测资料同样不可或缺。它们就像花卉生长的“日记”，记录着始花期、盛花期等重要信息。结合气象数据中的积温、光周期、冬季低温量等影响因素，我们可以像搭建积木一样，构建花卉花期预报模型。以油菜花为例，它对积温十分敏感，通过分析历史积温数据和油菜花花期数据之间的“亲密关系”，就能搭建起预测其花期的模型。

• 问题 3

  ：问题 1 的降雨预测和问题 2 的花期预测结果，是制定踏青赏花自由行攻略的“秘密武器”。将这些数据整合构建决策矩阵，就如同绘制一幅详细的作战地图，通过多目标优化算法，为游客制定出科学合理的攻略。比如，根据降雨概率和花期状态，挑选出“无雨 + 盛花期”的完美组合，同时兼顾交通成本，为游客规划出最佳的赏花路线。

• 问题 4

  ：问题 1 和 2 的结果，为制定延长“赏花经济”产业链的措施提供了坚实的基础。此外，还需考虑游客量弹性系数、二次消费转化率、品牌溢价效应等经济变量，这些变量如同经济舞台上的演员，共同演绎着经济效益的变化。通过建立经济效益模型，我们可以像导演一样，精准评估采取措施后可能为地方带来的经济效益。例如，通过分析历史游客量和天气数据，建立天气 - 客流量响应曲面，为制定更合理的产业链措施提供参考。

• 数据处理方法

  ：

• 数据清洗

  ：气象数据和花期数据可能存在缺失值和异常值，就像美玉上的瑕疵。对于缺失值，我们可以采用插值法，如线性插值、样条插值，像能工巧匠修复玉器一样，填充这些缺失的部分；对于异常值，通过设定合理的阈值，将其识别并妥善处理，确保数据的纯净与准确。

• 数据转换

  ：为了让数据更好地适配模型，我们需要对其进行转换。比如将日期数据转换为儒略日，就像给时间换上一件更适合分析的“外衣”，方便进行时间序列分析；对气象数据进行标准化处理，消除不同变量之间量纲的差异，让数据在同一“起跑线”上。

• 数据抽样

  ：当数据量庞大时，如同面对一片浩瀚的海洋，我们可以采用随机抽样的方法，从原始数据中抽取一部分样本进行分析，就像从海洋中舀取一瓢水，通过这瓢水来了解整个海洋的“味道”。

2.2 前后问题的整体逻辑

四个问题构成了一条紧密相连的“知识链”，从气象预测出发，逐步延伸到花期预报、旅游规划，最终落脚到经济决策。问题 1 是这条链的起点，通过对历史气象数据的抽丝剥茧，分析“雨纷纷”的规律，建立降雨预测模型，为后续问题筑牢天气基础。问题 2 基于问题 1 的气象预测结果，如同在天气的舞台上为花卉生长建模，揭示自然系统对气候的响应规律。问题 3 巧妙整合问题 1 和 2 的成果，通过多目标优化，为游客量身定制决策方案，就像为游客打造一把开启美好赏花之旅的钥匙。问题 4 则将自然科学结论转化为产业政策，完成“数据→知识→应用”的华丽转身，实现价值的闭环。

具体而言，问题 1 的降雨预测结果，如同给问题 2 提供了一把气候的“尺子”，影响着花卉花期的预测；问题 2 的花期预测结果，直接为问题 3 制定踏青攻略提供花期信息，成为攻略中的关键“景点”，同时也为问题 4 规划赏花经济产业链提供花期依据；问题 1 的降雨情况，还会像一个“天气精灵”，影响问题 3 攻略中对天气风险的评估，以及问题 4 中花卉生长和游客出行的考量。

2.3 问题一分析

• 问题起源、发展及与其他问题联系

  ：清明节，“雨纷纷”的景象深入人心，但不同地区降雨差异巨大。随着人们对清明假期出行需求的增长，准确判断各地是否“雨纷纷”变得至关重要，而气象学的发展为我们提供了实现这一目标的有力工具。问题 1 就像一座桥梁，为后续问题搭建起气象基础。问题 2 中花卉花期受降水等气象因子影响，需要借助问题 1 的降雨预测结果；问题 3 制定踏青攻略时，降雨情况是必须考虑的重要因素；问题 4 发展赏花经济，也离不开降雨对花卉生长和游客出行影响的考量。

• 解答思路

  ：

• 影响因素

  ：大气环流、海陆热力差异、地形抬升效应、城市热岛效应等因素，如同一个个幕后操纵者，共同影响着降雨情况。例如，副高位置的变动，就像指挥棒一样，影响着冷暖空气的交汇，进而决定降雨是否发生；地形抬升效应则像一个“降雨制造机”，使气流上升冷却，增加降雨的可能性。

• 理论基础

  ：基于气象学降水形成机制，我们可以运用时间序列分析（ARIMA）和机器学习（LSTM/随机森林）等方法，像搭建一座坚固的大厦一样，建立降雨预测模型。ARIMA 模型擅长处理具有周期性和趋势性的时间序列数据，就像一位经验丰富的工匠，能巧妙应对这类数据；LSTM 网络则像一个记忆力超群的智者，能够处理长序列数据，捕捉其中的长期依赖关系；随机森林算法如同一个高效的团队，可处理高维数据，具备良好的泛化能力。

• 核心变量

  ：日降水量、持续时长、相对湿度、850hPa 涡度场等核心变量，如同模型的“心脏”，对降雨起着关键作用。日降水量和持续时长直观地反映降雨的强度和持续时间；相对湿度就像降雨的“催化剂”，影响水汽含量，是降雨形成的重要条件；850hPa 涡度场则像一个“气象风向标”，反映大气的涡旋运动，与降雨紧密相关。

• 约束条件

  ：数据完整性（部分站点缺失）和预报时效性（需提前 30 天预测）是我们面临的两大挑战。部分站点数据缺失，如同拼图缺少了几块，可能影响模型的准确性，需要我们运用合适的方法进行填补；提前 30 天预测，则要求模型像一位精准的预言家，具备良好的稳定性和泛化能力。

• 模型构建

  ：采用两阶段建模的策略。第一阶段，建立分类模型判断是否“雨纷纷”。设输入变量为X=(x_1,x_2,\cdots,x_n)，其中x_i表示第i个特征变量，输出变量为Y，Y = 1表示“雨纷纷”，Y = 0表示非“雨纷纷”。可以使用逻辑回归、支持向量机等分类算法，像训练一支专业的分类队伍一样，进行建模。第二阶段，建立回归模型预测具体雨量。设输入变量为X，输出变量为Z，表示具体雨量。可以使用线性回归、随机森林回归等算法，像搭建一个精准的预测仪器一样，进行建模。

• 模型求解

  ：使用贝叶斯优化超参数，通过 Brier 评分评估概率预测效果。贝叶斯优化就像一个聪明的寻宝者，在参数空间中寻找最优的超参数组合，提高模型性能；Brier 评分则像一把精准的尺子，衡量概率预测的准确性，评分越低表示预测效果越好。

• 解答过程注意事项

  ：

• 数据精度

  ：确保数据的准确性和精度，如同守护一座宝藏，对数据进行严格的质量控制。在处理缺失值和异常值时，要像挑选珍贵宝石一样，选择合适的方法，避免对模型造成不良影响。

• 模型假设合理性

  ：在建立模型时，要确保模型的假设符合实际情况，就像建造房屋要符合地质条件一样。例如，在使用 ARIMA 模型时，要检验数据是否满足平稳性假设；在使用机器学习模型时，要考虑特征变量之间的相关性。

• 计算方法选择

  ：根据数据的特点和模型的要求，选择合适的计算方法，如同为不同的任务挑选合适的工具。例如，在进行贝叶斯优化时，要选择合适的优化算法和参数；在进行模型求解时，要考虑计算效率和内存占用。

• 总结

  ：

• 首先，结合气象标准和文学意境，像给一个神秘的概念下定义一样，明确“雨纷纷”的量化定义。

• 然后，从 NOAA 和 RP5 等数据源提取近 20 年清明期间的气象数据，进行数据清洗和预处理，如同对一块粗糙的玉石进行雕琢。

• 接着，选择合适的模型（如 ARIMA、随机森林、LSTM）建立降雨预测模型，使用贝叶斯优化超参数，像为模型挑选最适合的装备。

• 再用 2025 年清明实况数据验证模型的合理性，通过 Brier 评分等指标评估模型的性能，如同对一件产品进行质量检测。

• 最后，给出利用最新天气实况进行模型修正的方法，如贝叶斯更新、卡尔曼滤波等，像为模型注入新的活力，使其更加精准。

2.4 问题二分析

• 问题起源、发展及与其他问题联系

  ：清明时节花卉盛开，然而花期的不确定性，就像一团迷雾，给人们的赏花计划带来困扰。为了拨开这团迷雾，让人们更好地规划赏花行程，建立花卉花期预报模型就显得尤为重要。该问题如同一位“花之使者”，直接服务于问题 3 和问题 4。问题 3 制定踏青攻略需要知道花卉的开放时间和花期，就像旅行者需要知道景点的开放时间；问题 4 发展赏花经济需要准确把握花期，以便合理安排产业链活动，如同商家需要了解商品的上市时间。

• 解答思路

  ：

• 影响因素

  ：积温、光周期、冬季低温量、极端天气事件等因素，如同花卉生长的“魔法棒”，影响着花卉的花期。例如，积温是花卉生长发育的重要“能量源”，不同花卉对积温的要求各不相同；光周期像一个“时间调节器”，影响花卉的花芽分化和开花时间；冬季低温量满足春化作用，是一些花卉开花的必要“通行证”。

• 理论基础

  ：基于物候学积温定律、Chuine 模型和机器学习特征重要性分析等方法，我们可以像搭建一个花卉生长的“智慧舞台”，建立花期预报模型。物候学积温定律认为植物的生长发育需要一定的积温，就像汽车行驶需要一定的燃料；Chuine 模型考虑了温度和光照等因素，如同一个全面的“花期计算器”；机器学习特征重要性分析则像一个“寻宝探测器”，帮助我们识别影响花期的主导因子。

• 核心变量

  ：始花期 JD（儒略日）、盛花期持续天数、花前 30 天气象要素是核心变量，它们如同花卉花期的“密码锁”。始花期和盛花期持续天数直接揭示花卉的花期情况，花前 30 天气象要素（如积温、日照时数、降水等）则像一把把钥匙，对花卉的开花时间起着关键作用。

• 约束条件

  ：品种差异（如早/晚樱）和观测数据稀疏性（需文献挖掘补充）是我们面临的两大难题。不同品种的花卉花期可能大相径庭，需要分别建立模型进行预测，就像为不同的学生制定个性化的学习计划；观测数据稀疏可能影响模型的准确性，需要通过文献挖掘等方式补充数据，如同为一幅不完整的拼图寻找缺失的部分。

• 模型构建

  ：分物种建立预测模型。对于油菜花，因其对积温敏感，可使用 Logistic 回归模型进行建模，就像为油菜花量身定制一个“花期预测仪”。设输入变量为X=(x_1,x_2,\cdots,x_n)，其中x_i表示第i个特征变量，输出变量为Y，表示油菜花的始花期。Logistic 回归模型的公式为：P(Y = 1|X)=\frac{1}{1 + e^{-(β_0 + β_1x_1 + \cdots + β_nx_n)}}，其中β_0,β_1,\cdots,β_n是模型的参数。对于樱花，由于其受多因子交互影响，可使用 XGBoost 模型进行建模，如同为樱花打造一个“智能花期预测系统”。XGBoost 是一种梯度提升树模型，通过迭代训练多个决策树来提高模型的性能。

• 模型求解

  ：采用 SHAP 值解释模型，通过交叉验证防止过拟合。SHAP 值像一个“模型翻译官”，可以解释模型的预测结果，帮助我们理解每个特征变量对花期预测的贡献；交叉验证则像一个“质量监督者”，评估模型的泛化能力，避免模型在训练集上表现良好，但在测试集上表现不佳的情况。

• 解答过程注意事项

  ：

• 数据精度

  ：确保花期数据和气象数据的准确性和精度，如同守护珍贵的文物，对数据进行严格的质量控制。在处理花期数据时，要注意不同观测方法和标准的差异，就像对待不同版本的古籍，要仔细甄别。

• 模型假设合理性

  ：在建立模型时，要确保模型的假设符合实际情况，如同设计一款产品要符合用户需求。例如，在使用物候学积温定律时，要考虑不同花卉对积温的响应差异；在使用机器学习模型时，要考虑特征变量之间的非线性关系。

• 计算方法选择

  ：根据数据的特点和模型的要求，选择合适的计算方法，如同为不同的烹饪任务挑选合适的厨具。例如，在进行 XGBoost 模型训练时，要选择合适的参数和优化算法；在进行交叉验证时，要选择合适的折数和评估指标。

• 总结

  ：

• 先选择地域代表性强、数据易获取的 2 - 3 种花卉，如同挑选最具特色的“花之明星”。

• 然后，收集气象数据（积温、日照时数、降水等）和花期数据（始花期、盛花期记录），进行数据清洗和预处理，如同为“花之明星”整理妆容。

• 接着，分物种建立预测模型，如油菜花使用 Logistic 回归模型，樱花使用 XGBoost 模型，为每朵花打造专属的“花期预测秘籍”。

• 采用 SHAP 值解释模型，通过交叉验证防止过拟合，像为秘籍配上详细的解读和严格的检验。

• 最后，输出 2026 年这些花卉的预测花期，对 2026 年预测需考虑气候变化趋势（加入 CMIP6 预估数据修正），如同为花期预测加上与时俱进的“智慧翅膀”。

2.5 问题三分析

• 问题起源、发展及与其他问题联系

  ：随着文旅产业的蓬勃发展，清明假期成为人们踏青赏花的热门时段。然而，天气和花期的不确定性，就像隐藏在旅途中的“小怪兽”，可能影响游客的赏花体验。为了帮助游客避开这些“小怪兽”，制定一份科学合理的踏青赏花自由行攻略迫在眉睫。该问题依赖于问题 1 的降雨预测和问题 2 的花期预测结果，如同站在两位巨人的肩膀上，通过整合这两个问题的信息，进行动态匹配和多目标优化，为游客绘制出最佳的赏花路线图。

• 解答思路

  ：

• 目标函数

  ：我们的目标是最大化花期观赏指数，同时最小化天气风险系数和交通成本，就像在一场复杂的游戏中寻找最优策略。设花期观赏指数为I，天气风险系数为R，交通成本为C，则目标函数为max\{I\} - λ·R - μ·C，其中λ和μ是权重系数，如同游戏中的调节按钮，用于调整各目标的重要程度。

• 决策变量

  ：决策变量包括目的地组合、游览日期序列、交通方式选择，它们如同游戏中的关键选项。设目的地集合为D=\{d_1,d_2,\cdots,d_m\}，游览日期集合为T=\{t_1,t_2,\cdots,t_n\}，交通方式集合为M=\{m_1,m_2,\cdots,m_k\}，则决策变量可以表示为(d_{i_1},t_{j_1},m_{l_1}),(d_{i_2},t_{j_2},m_{l_2}),\cdots。

• 约束条件

  ：总预算限制、最大移动距离（300km/日）、景点开放时间是我们在游戏中需要遵守的规则。设总预算为B，交通成本矩阵为C_{ij}，表示从目的地d_i到目的地d_j的交通成本，则总预算限制可以表示为\sum_{i = 1}^{s}C_{i,i + 1}\leq B；最大移动距离限制可以表示为dist(d_{i},d_{i + 1})\leq 300，其中dist(d_{i},d_{i + 1})表示目的地d_i到目的地d_{i + 1}的距离；景点开放时间限制需要根据实际情况进行考虑，确保我们的游戏能够顺利进行。

• 模型构建

  ：构建三维决策矩阵（城市×日期×花卉状态），将问题转化为混合整数规划问题，如同将游戏规则转化为数学语言。设决策变量x_{ijkl}表示在日期t_j选择目的地d_i，花卉状态为k，交通方式为m_l的决策，x_{ijkl}=1表示选择，x_{ijkl}=0表示不选择。则目标函数和约束条件可以表示为线性规划的形式，通过求解线性规划问题得到最优解，找到游戏的最佳策略。

• 求解算法

  ：使用自适应大邻域搜索（ALNS）算法，动态调整λ权重，如同在游戏中根据实际情况灵活调整策略。ALNS 算法是一种启发式算法，通过不断搜索邻域解来寻找最优解；动态调整λ权重可以根据不同游客的需求和偏好，调整天气风险和花期观赏指数的重要程度，满足不同游客的游戏需求。

• 解答过程注意事项

  ：

• 数据精度

  ：确保降雨预测数据和花期预测数据的准确性和精度，如同确保游戏信息的真实性，对数据进行严格的质量控制。在处理交通成本数据时，要考虑不同交通方式的价格波动和实际情况，就像在游戏中要考虑各种道具的实际价值。

• 模型假设合理性

  ：在建立模型时，要确保模型的假设符合实际情况，如同游戏规则要符合现实逻辑。例如，在计算花期观赏指数时，要考虑花卉的生长状态和观赏效果；在考虑天气风险系数时，要考虑不同游客对天气的耐受程度。

• 计算方法选择

  ：根据问题的规模和复杂度，选择合适的计算方法，如同根据游戏的难度选择合适的通关技巧。例如，在使用 ALNS 算法时，要选择合适的邻域结构和搜索策略；在求解线性规划问题时，要选择合适的求解器。

• 总结

  ：

• 整合问题 1 的降雨预测和问题 2 的花期预测结果，构建决策矩阵（城市×日期×（降雨概率, 花期状态, 交通成本）），如同绘制一幅详细的游戏地图。

• 确定目标函数和约束条件，将问题转化为混合整数规划问题，明确游戏规则。

• 使用自适应大邻域搜索（ALNS）算法，动态调整λ权重，求解最优解，在游戏中找到最佳策略。

• 输出帕累托前沿解集，包括保守型（低风险）、均衡型、冒险型（高观赏性）等不同类型的方案，为游客提供推荐路线和备用方案，就像为玩家提供多种游戏通关攻略。

2.6 问题四分析

• 问题起源、发展及与其他问题联系

  ：赏花经济作为文旅产业的一颗璀璨明珠，具有巨大的发展潜力。然而，目前其产业链较短，花期有限，就像一朵尚未完全绽放的花朵。为了让这朵花绽放得更加绚烂，地方政府需要采取措施延长产业链，实现可持续发展。该问题基于问题 1 的气象分析和问题 2 的花期预测，如同站在气象和花期的“瞭望塔”上，制定延长花期和促进衍生消费的措施。通过建立经济效益模型，评估这些措施对地方经济的影响，为政府决策提供科学依据，就像为政府提供一本发展赏花经济的“指南”。

• 解答思路

  ：

• 产业链措施

  ：从时间维度和空间维度为产业链发展出谋划策。时间维度上，采用早/晚花品种搭配和温室调控的方法，如同为花卉生长安排一个巧妙的“时间表”，延长花期；空间维度上，建设花卉主题综合体，促进衍生消费，就像为游客打造一个丰富多彩的“花卉乐园”。

• 经济变量

  ：考虑游客量弹性系数（1.2 - 1.8）、二次消费转化率（15 - 40%）、品牌溢价效应等经济变量，它们如同经济发展的“引擎”。游客量弹性系数表示游客量对价格、天气等因素的敏感程度，就像汽车对不同路况的反应；二次消费转化率表示游客在景区内进行二次消费的比例，反映了景区的消费潜力；品牌溢价效应表示品牌知名度对游客吸引力和消费意愿的影响，如同品牌的“魔力光环”。

• 模型构建

  ：建立系统动力学模型，考虑正反馈和负反馈机制，如同构建一个经济运行的“动态模拟器”。正反馈机制为媒体曝光→知名度→客流量，负反馈机制为拥挤效应。设游客量为V，知名度为P，媒体曝光量为E，拥挤效应系数为α，则系统动力学模型可以表示为一组微分方程：\frac{dV}{dt}=f(V,P,E,α)，\frac{dP}{dt}=g(V,P,E)。

• 参数校准

  ：采用蒙特卡洛模拟处理参数不确定性，参考同类景区历史数据，如同为“动态模拟器”校准参数。蒙特卡洛模拟可以通过随机抽样的方法，模拟不同参数组合下的系统行为，评估参数不确定性对模型结果的影响；参考同类景区历史数据可以提高参数校准的准确性，让“模拟器”更加贴近实际。

• 效益指标

  ：考虑直接经济收益（门票等）、间接收益（餐饮住宿）、就业乘数效应等效益指标，它们如同衡量经济发展的“标尺”。直接经济收益可以通过门票价格和游客量计算得到，间接收益可以通过游客在景区内的消费情况计算得到，就业乘数效应表示旅游业对就业的带动作用，全面评估赏花经济的效益。

• 敏感性分析

  ：重点考察游客量对天气敏感度，建立天气 - 客流量响应曲面，如同绘制一张游客量与天气关系的“地图”。通过分析不同天气条件下游客量的变化情况，了解游客对天气的敏感度，为制定产业链措施提供参考，让措施更加精准有效。

• 解答过程注意事项

  ：

• 数据精度

  ：确保气象数据、花期数据、经济数据的准确性和精度，如同确保“标尺”的精准度，对数据进行严格的质量控制。在处理游客量数据时，要考虑不同年份、不同季节的波动情况，就像测量物体时要考虑环境因素的影响。

• 模型假设合理性

  ：在建立模型时，要确保模型的假设符合实际情况，如同设计一个机器要符合工作原理。例如，在考虑正反馈和负反馈机制时，要考虑实际的市场情况和游客行为；在进行参数校准时，要考虑不同景区的特点和差异。

• 计算方法选择

  ：根据问题的特点和模型的要求，选择合适的计算方法，如同为不同的工作选择合适的工具。例如，在进行蒙特卡洛模拟时，要选择合适的抽样方法和模拟次数；在求解系统动力学模型时，要选择合适的数值解法。

• 总结

  ：

• 根据问题 1 和问题 2 的结果，提出延长花期（如温室调控、品种搭配）和促进衍生消费（如文创产品、花节 IP）的产业链措施，为赏花经济注入新的活力。

• 建立经济效益模型，以游客量、人均消费、成本等为变量，运用系统动力学模拟政策干预对地方经济的影响，像为赏花经济的发展搭建一个“虚拟实验室”。

• 采用蒙特卡洛模拟处理参数不确定性，参考同类景区历史数据进行参数校准，让“虚拟实验室”更加贴近现实。

• 分析直接经济收益、间接收益、就业乘数效应等效益指标，进行敏感性分析，重点考察游客量对天气敏感度，全面评估赏花经济的效益和风险。

• 为地方政府提供具体的产业链措施和经济效益评估结果，为政府决策提供科学依据，成为政府发展赏花经济的得力“参谋”。

通过对以上四个问题的详细分析，我们如同绘制了一幅数学建模的“作战蓝图”，明确了每个问题的解决思路和方法。希望同学们在建模过程中能够充分发挥自己的智慧，结合实际情况，完成高质量的数学建模作品，在这场知识与智慧的挑战中取得优异成绩。

import numpy as np import pandas as pdfrom sklearn.preprocessing import MinMaxScaler from tensorflow.keras.modelsimportSequential from tensorflow.keras.layers import LSTM, Dense#  生成模拟的天气数据（降水量）data = np.random.rand(365, 1)  # 假设每年 365 天的数据# 数据标准化scaler = MinMaxScaler(feature_range=(0, 1)) data_scaled= scaler.fit_transform(data)#  创建时间序列数据def create_dataset(data,look_back=1): X, Y = [], []for i in range(len(data)-look_back):X.append(data[i:i+look_back, 0])Y.append(data[i+ look_back, 0])return np.array(X), np.array(Y)look_back = 10X, Y = create_dataset(data_scaled,look_back)# Reshape输入为 LSTM 的 [样本数，时间步，特征数]X = X.reshape(X.shape[0], X.shape[1], 1)# 构建 LSTM 模型model = Sequential()model.add(LSTM(units=50, return_sequences=False, input_shape=(X.shape[1], 1)))model.add(Dense(1))model.compile(optimizer='adam', loss='mean_squared_error')#训练模型model.fit(X, Y, epochs=20, batch_size=32)# 使用模型进行预测predicted = model.predict(X)# 反向转换预测结果predicted = scaler.inverse_transform(predicted) print(predicted)

2025年第十届数维杯数学建模挑战赛C题论文Word+代码结果https://download.csdn.net/download/qq_52590045/90778347

 ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓