《现代控制理论》 刘豹 第三章

目录

3.1 能控性的定义

3.2 线性定常系统的能控性判别

3.2.1 具有约旦标准型系统的能控性判别 

3.2.2 直接从A到B判别系统的能控性

3.3 线性连续定常系统的能观性 

3.3.1 能观性定义

 3.3.2 定常系统能观性的判别

 ​

 3.4 离散时间系统的能控性和能观性

3.4.1 能控性矩阵M

3.4.2 能观性矩阵N

 ​

3.5 时变系统的能控性和能观性

3.5.1 能控性判别

 3.5.3 连续时变系统可控性和可观性判别法则和连续定常系统的判别法之间的关系

3.6 能控性和能观性的对偶关系

3.6.1 线性系统的对偶关系

3.6.2 对偶原理

3.6.3 时变系统的对偶原理

 3.7 状态空间表达式的能控标准型和能观标准型

3.7.1 单输入系统的能控标准型

 ​

 3.7.2 单输入系统的能观标准型

 3.8 线性系统的结构分解

3.8.1 按能控性分解

 3.8.2 按能观性分解

3.8.3 按能控性和能观性进行分解

 3.9 传递函数阵的实现问题

3.9.1 实现问题的基本概念

3.9.2 能控标准型实现和能观标准型实现

 3.9.3 最小实现

 3.10 传递函数中零极点对消与状态能控能观性之间的关系

---

3.1 能控性的定义

能控性考察系统在控制作用的控制下，状态矢量的转移情况，而与输出无关。

1.线性连续定常系统的能控性定义

关键词：存在一个分段连续输入 ;有限时间区间[,];指定的任一终端状态

能达性：将上述初始化为0

2.线性连续时变系统的能控性定义

应强调在时刻系统是能控的。

3.离散时间系统

看书

3.2 线性定常系统的能控性判别

3.2.1 具有约旦标准型系统的能控性判别 

1. 单输入系统 

 

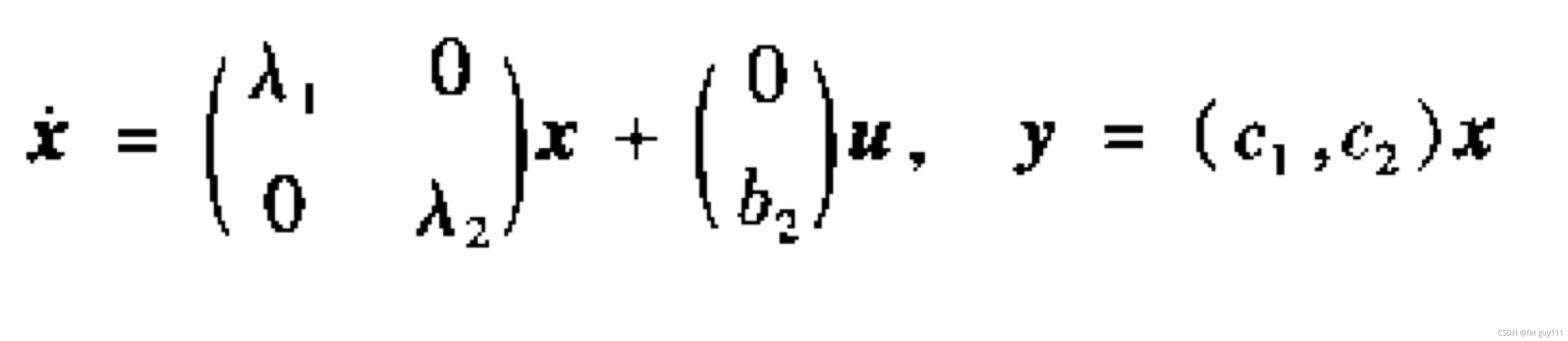
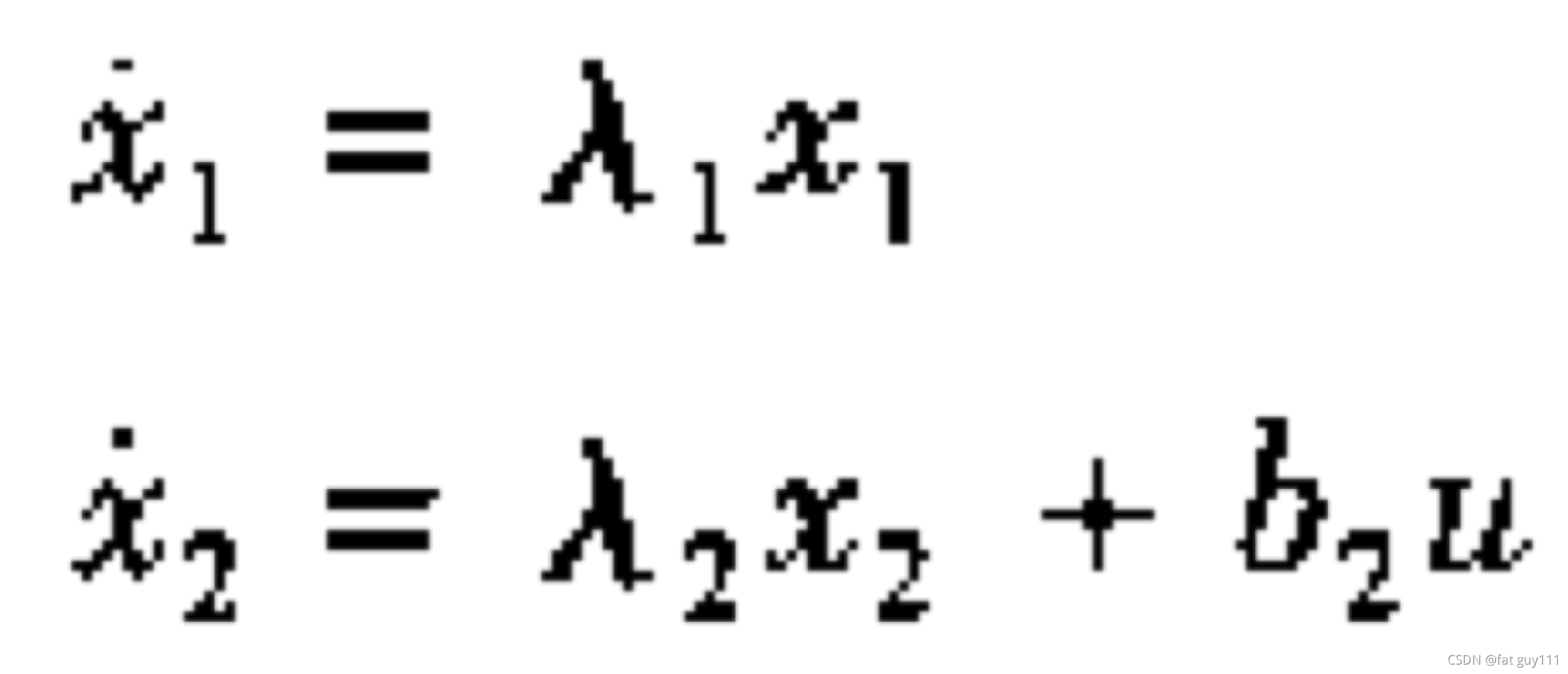
 可以受控制量u的控制，但和u无关。所以是不能控系统。

---

---

 

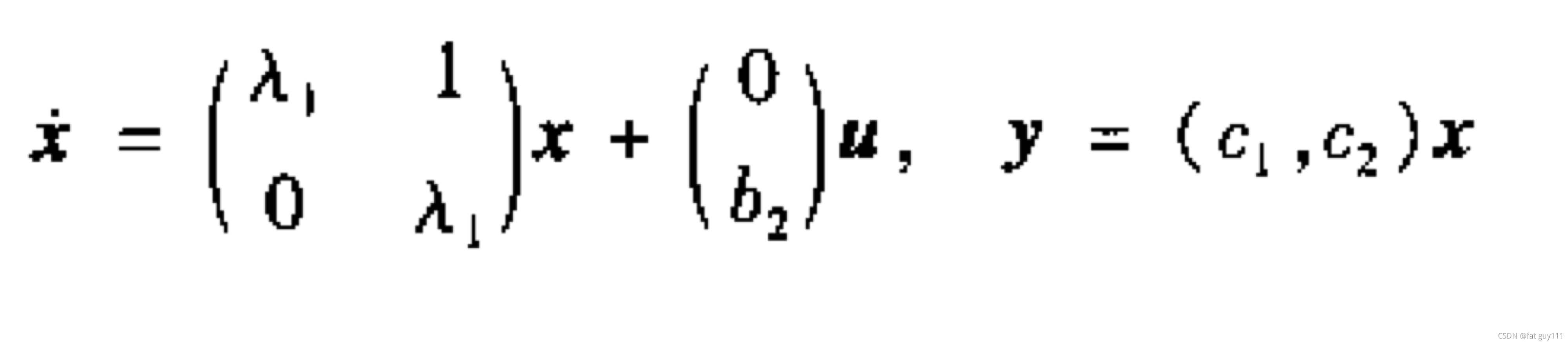
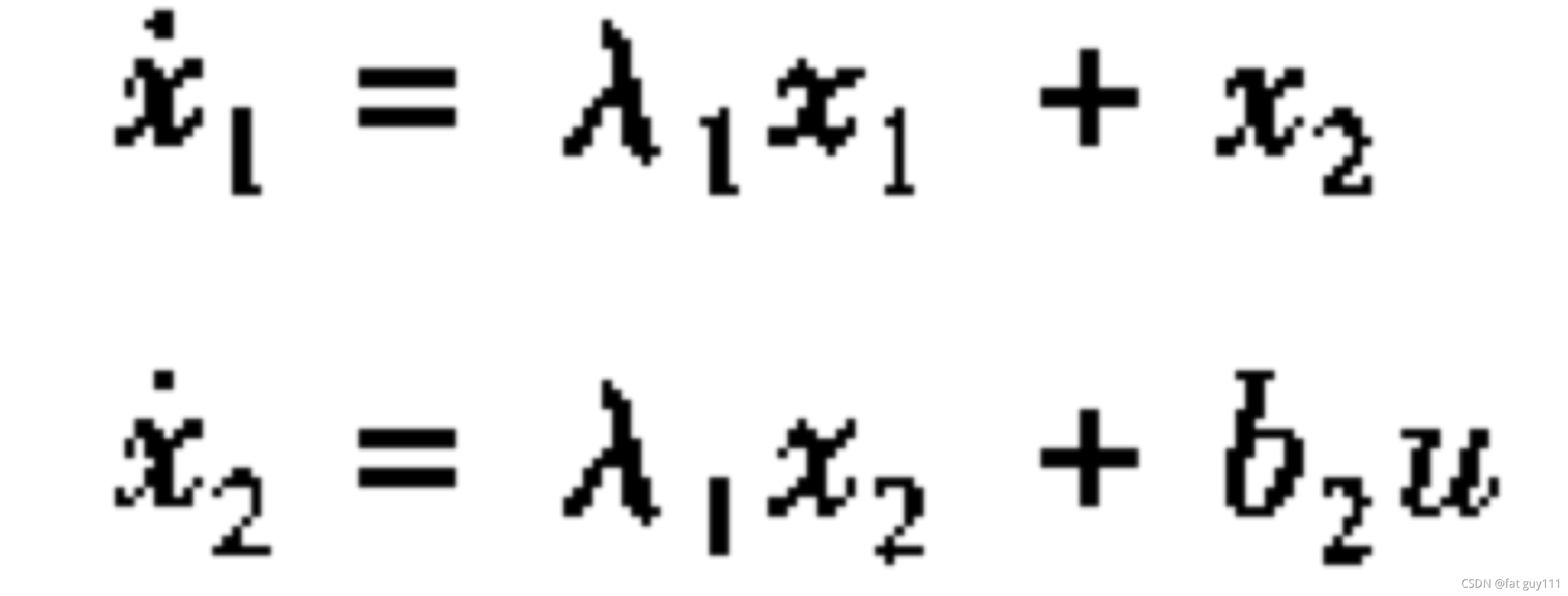
 这是一个状态完全能控的系统

---

---

 

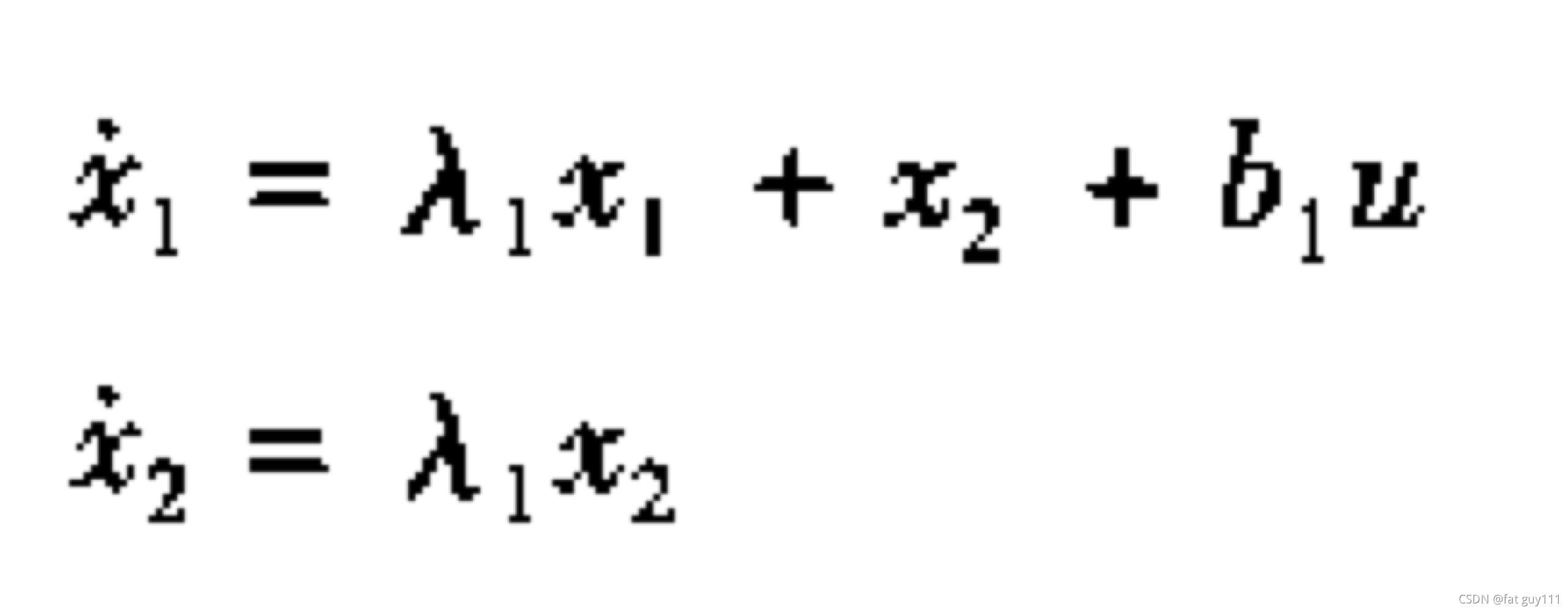
 不能控系统

2. 具有一般系统矩阵的多输入系统 

前提：系统的线性变换不改变系统的能控性条件

一般系统的能控性判据：

若A的特征值互异，变换成约旦矩阵，充要条件：控制矩阵的各行元素没有全是0的

若A的特征值有相同

1. 在中对应于相同特征值的部分，它与每个约旦块最后一行相对应的一行元素没有全是0的

2. 中对于互异特征值部分，它的各行元素没有全是0的

 典型系统：是能控的。

3.2.2 直接从A到B判别系统的能控性

1. 单输入系统 

对,其能控的充分必要条件是由A，b 构成的能控性矩阵：满秩，即rankM=n. 若rankM<n,系统不能控。

同时，也可以根据u——x间的传递函数阵  在这种情况下，状态完全能控的充要条件是没有零极点重合现象。

2. 多输入系统 

和上述单输入系统的能控充要条件类似，将b换为B即可

常用来代替计算M的秩

3.3 线性连续定常系统的能观性 

3.3.1 能观性定义

能观性表示输出