大语言模型的模型量化(INT8/INT4)技术

最新推荐文章于 2025-03-08 00:15:00 发布

seetimee

最新推荐文章于 2025-03-08 00:15:00 发布

阅读量3.6k

点赞数 49

分类专栏：大模型部署文章标签：算法人工智能

本文链接：https://blog.csdn.net/stephen147/article/details/141031918

版权

一、LLM.in8 的量化方案
1. 1.1 模型量化的动机和原理
2. 1.2 LLM.int8 量化的精度和性能
3. 1.3 LLM.int8 量化的实践
二、SmoothQuant 量化方案
1. 2.1 SmoothQuant 的基本原理
2. 2.2 SmoothQuant 的实践
三、GPTQ 量化训练方案
1. 3.1 GPTQ 的基本原理
2. 3.2 GPTQ 的实践
参考资料

一、LLM.in8 的量化方案

1.1 模型量化的动机和原理

成本和准确度。

常见精度介绍：大模型涉及到的精度是啥？FP32、TF32、FP16、BF16、FP8、FP4、NF4、INT8区别

在训练时，为保证精度，主权重始终为 FP32。而在推理时，FP16 权重通常能提供与 FP32 相似的精度，这意味着在推理时使用 FP16 权重，仅需一半 GPU 显存就能获得相同的结果。那么是否还能进一步减少显存消耗呢？答案就是使用量化技术，最常见的就是 INT8 量化。

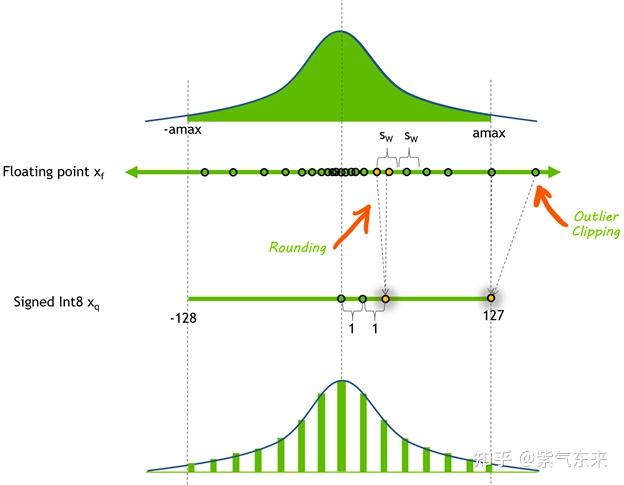
简单来说， INT8 量化即将浮点数 $x_f$ 通过缩放因子 $sc a l e$ 映射到范围在[-128, 127] 内的 8bit 表示 $x_q$ ，即

$x_q=\operatorname{Clip}\left(\operatorname{Round}\left(x_f * \text { scale }\right)\right)$

其中 Round 表示四舍五入都整数，Clip 表示将离群值(Outlier) 截断到 [-128, 127] 范围内。对于 scale 值，通常按如下方式计算得到：

$\begin{aligned} &amax =\max \left(a b s\left(x_f\right)\right)\\ &\text { scale }=127/amax \end{aligned}$

反量化的过程为：

$x_f^{'} = x_q/scale$

下面是通过该方式实现的量化-反量化的例子：

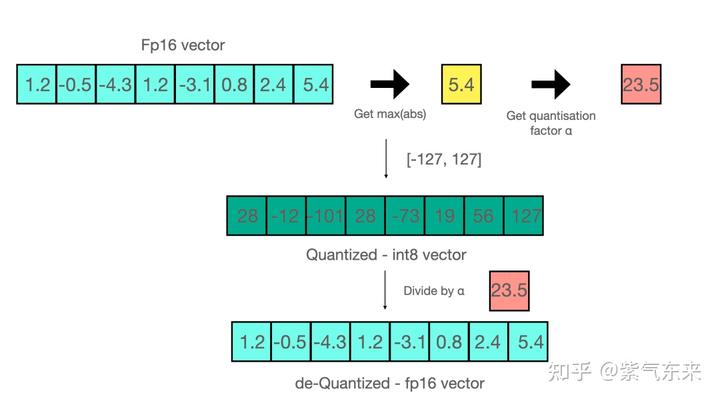
当进行矩阵乘法时，可以通过组合各种技巧，例如逐行或逐向量量化，来获取更精确的结果。举个例子，对矩阵乘法，我们不会直接使用常规量化方式，即用整个张量的最大绝对值对张量进行归一化，而会转而使用向量量化方法，找到 A 的每一行和 B 的每一列的最大绝对值，然后逐行或逐列归一化 A 和 B 。最后将 A 与 B 相乘得到 C。最后，我们再计算与 A 和 B 的最大绝对值向量的外积，并将此与 C 求哈达玛积来反量化回 FP16。

1.2 LLM.int8 量化的精度和性能

上文说明了如何对单个向量进行量化，原理比较简单，但是可能也会出现一些问题，比如下面这个例子：

A=[-0.10, -0.23, 0.08, -0.38, -0.28, -0.29, -2.11, 0.34, -0.53, -67.0]

注意到向量A中有离群值(Emergent Features) $- 67.0$ ，如果去掉该值对向量A做量化和反量化，处理后的结果是：

[-0.10, -0.23, 0.08, -0.38, -0.28, -0.28, -2.11, 0.33, -0.53]

出现的误差只有-0.29 -> -0.28。但是如果我们在保留 $- 67.0$ 的情况下对该向量做量化和反量化，处理后的结果是：

[ -0.00, -0.00, 0.00, -0.53, -0.53, -0.53, -2.11, 0.53, -0.53, -67.00]

可见大部分信息在处理后都丢失了。

幸运的是，Emergent Features的分布是有规律的。对于一个参数量为6.7亿的transformer模型来说，每个句子的表示中会有150000个Emergent Features，但这些Emergent Features只分布在6个维度中

基于此，可以采用混合精度分解的量化方法：将包含了Emergent Features的几个维度从矩阵中分离出来，对其做高精度的矩阵乘法；其余部分进行量化。如下图所示：

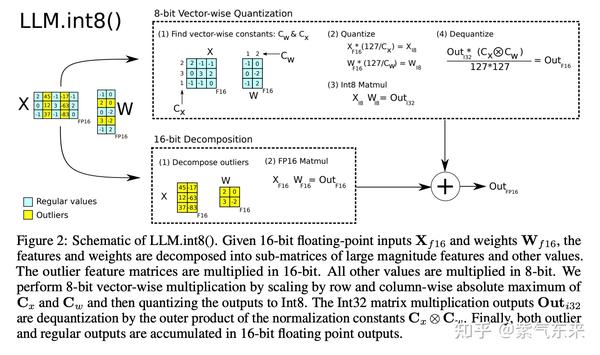
精度与性能

如下图所示的对比实验，可以看到，在模型参数量达到6.7亿时，使用vector-wise方法进行量化会使模型性能有非常大的下降，而使用LLM.int8()方法进行量化则不会造成模型性能的下降。

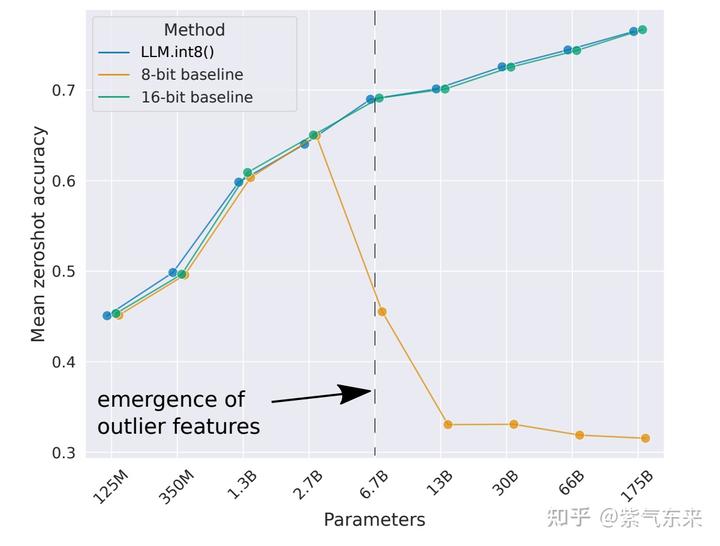
对 OPT-175B 模型，使用 lm-eval-harness 在 8 位和原始模型上运行了几个常见的基准测试，结果如下：

测试基准	-	-	-	-	-
测试基准名	指标	指标值 int8	指标值 fp16	标准差 fp16	指标差值
hellaswag	acc_norm	0.7849	0.7849	0.0041	0
hellaswag	acc	0.5921	0.5931	0.0049	0.001
piqa	acc	0.7965	0.7959	0.0094	0.0006
piqa	acc_norm	0.8101	0.8107	0.0091	0.0006
lambada	ppl	3.0142	3.0152	0.0552	0.001
lambada	acc	0.7464	0.7466	0.0061	0.0002
winogrande	acc	0.7174	0.7245	0.0125	0.0071

LLM.int8() 方法的主要目的是在不降低性能的情况下降低大模型的应用门槛，使用了 LLM.int8() 的 BLOOM-176B 比 FP16 版本慢了大约 15% 到 23%，结果如下所示：

精度	参数量	硬件	延迟 (ms/token，BS=1)	延迟 (ms/token，BS=8)	延迟 (ms/token，BS=32)
bf16	176B	8xA100 80GB	239	32	9.9
int8	176B	4xA100 80GB	282	37.5	10.2
bf16	176B	14xA100 40GB	285	36.5	10.4
int8	176B	5xA100 40GB	367	46.4	oom
fp16	11B	2xT4 15GB	11.7	1.7	0.5
int8	11B	1xT4 15GB	43.5	5.3	1.3
fp32	3B	2xT4 15GB	45	7.2	3.1
int8	3B	1xT4 15GB	312	39.1	10.2

1.3 LLM.int8 量化的实践

bitsandbytes 是基于 CUDA 的主要用于支持 LLM.int8() 的库。它是torch.nn.modules的子类，你可以仿照下述代码轻松地将其应用到自己的模型中。

首先导入模块，初始化fp16 模型并保存

import torch
import torch.nn as nn
from bitsandbytes.nn import Linear8bitLt

fp16_model = nn.Sequential(
    nn.Linear(64, 64),
    nn.Linear(64, 64)
).to(torch.float16).to(0)
torch.save(fp16_model.state_dict(), "model.pt")

初始化 int8 模型并加载保存的weight，此处标志变量has_fp16_weights非常重要。默认情况下，它设置为True，用于在训练时使能 Int8/FP16 混合精度。

int8_model = nn.Sequential(
    Linear8bitLt(64, 64, has_fp16_weights=False),
    Linear8bitLt(64, 64, has_fp16_weights=False)
)

int8_model.load_state_dict(torch.load("model.pt"))

此时还未进行量化操作，可以查看weight值

int8_model[0].weight
Parameter containing:
Parameter(Int8Params([[ 0.1032,  0.0544,  0.1021,  ..., -0.0465,  0.1050,  0.0687],
            [ 0.0083,  0.0352,  0.0540,  ..., -0.0931, -0.0224,  0.0541],
            [ 0.0476,  0.0220, -0.0803,  ...,  0.1031,  0.1134,  0.0905],
            ...,
            [-0.0523, -0.0858,  0.0330,  ...,  0.1122, -0.1082,  0.1210],
            [ 0.0045, -0.1019,  0.0072,  ..., -0.1069, -0.0417,  0.0365],
            [-0.1134,  0.0032, -0.0742,  ..., -0.1142, -0.0374,  0.0915]]))

之后将模型加载到GPU上，此时发生量化操作：

int8_model = int8_model.to(0) # Quantization happens here

此时可以查看weight值，可以看到值已经传到GPU上并转为 INT8 类型。

int8_model[0].weight
Parameter containing:
Parameter(Int8Params([[ 105,   55,  104,  ...,  -47,  107,   70],
            [   9,   36,   56,  ...,  -96