*12.6 函数项级数的一致收敛性及一致收敛级数的基本性质

12.6 函数项级数的一致收敛性及一致收敛级数的基本性质

第六节 函数项级数的一致收敛性及一致收敛级数的基本性质

一、函数项级数的一致收敛性

我们知道，有限个连续函数的和仍然是连续函数，有限个函数的和的导数及积分也分别等于它们的导数及积分的和。但是对于无穷多个函数的和是否也具有这些性质呢？换句话说，无穷多个连续函数的和 s(x)s(x)s(x) 是否仍然是连续函数？无穷多个函数的导数及积分的和是否仍然分别等于它们的和函数的导数及积分呢？我们曾经指出，对于幂级数来说，回答是肯定的。但是，对于一般的函数项级数是否都是如此呢？下面来看一个例子。

例1

函数项级数

的每一项都在 [0,1][0,1][0,1] 上连续，其前 nnn 项之和为 sn(x)=xns_n(x) = x^nsn​(x)=xn，因此和函数为

这和函数 s(x)s(x)s(x) 在 x=1x = 1x=1 处间断。由此可见，函数项级数的每一项在 [a,b][a,b][a,b] 上连续，并且级数在 [a,b][a,b][a,b] 上收敛，其和函数不一定在 [a,b][a,b][a,b] 上连续。也可以举出这样的例子，函数项级数的每一项的导数及积分所成的级数的和并不等于它们的和函数的导数及积分。这就提出了这样一个问题：对什么级数，能够从级数每一项的连续性得出它的和函数的连续性，从级数的每一项的导数及积分所成的级数之和得出原来级数的和函数的导数及积分呢？要回答这个问题，就需要引入下面的函数项级数的一致收敛性概念。

设函数项级数

在区间 III 上收敛于和 s(x)s(x)s(x)。也就是对于区间 III 上的每一个值 x0x_0x0​，数项级数

收敛于 s(x0)s(x_0)s(x0​)，即级数的部分和所成的数列

按数列极限的定义，对于任意给定的正数 ϵ\epsilonϵ 以及区间 III 上的每一个值 x0x_0x0​，都存在着一个正整数 NNN，使得当 n>Nn > Nn>N 时，有不等式 即

这个数 NNN 一般说来不仅依赖于 ϵ\epsilonϵ，而且也依赖于 x0x_0x0​。我们记它为 N(x0,ϵ)N(x_0, \epsilon)N(x0​,ϵ)。如果对于某一函数项级数能够找到这样一个正整数 NNN，它只依赖于 ϵ\epsilonϵ 而不依赖于 x0x_0x0​，也就是对区间 III 上的每一个值 x0x_0x0​ 都能适用的 N(ϵ)N(\epsilon)N(ϵ)，对这类级数我们给一个特殊的名称以区别于一般的收敛级数，这就是下面的一致收敛的定义。

定义

设有函数项级数 u1(x)+u2(x)+⋯+un(x)+⋯u_1(x) + u_2(x) + \cdots + u_n(x) + \cdotsu1​(x)+u2​(x)+⋯+un​(x)+⋯ 在区间 III 上收敛于和 s(x)s(x)s(x)。如果对于任意给定的正数 ϵ\epsilonϵ，都存在着一个只依赖于 ϵ\epsilonϵ 的正整数 NNN，使得当 n>Nn > Nn>N 时，对区间 III 上的一切 xxx，都有不等式 那么称函数项级数在区间 III 上一致收敛于 s(x)s(x)s(x)。

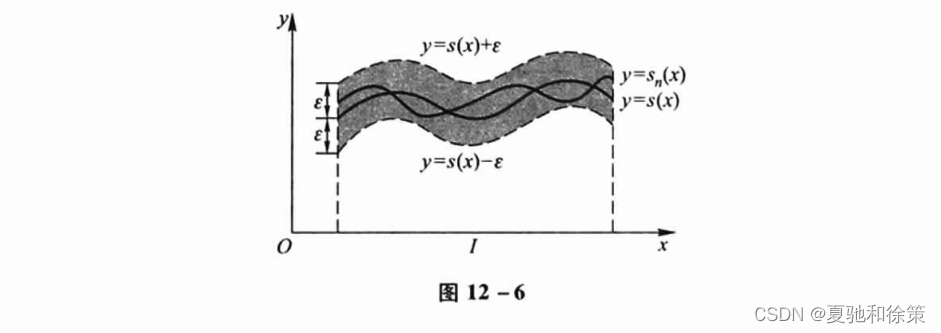
以上函数项级数一致收敛的定义在几何上可解释为：只要 nnn 充分大 (n>Nn > Nn>N)，在区间 III 上的所有曲线 y=sn(x)y = s_n(x)y=sn​(x) 将位于曲线 y=s(x)+ϵy = s(x) + \epsilony=s(x)+ϵ 与 y=s(x)−ϵy = s(x) - \epsilony=s(x)−ϵ 之间（图 12-6）。

例2

研究级数 在区间 [0,+∞)[0, +\infty)[0,+∞) 上的一致收敛性。

解答：

级数的前 nnn 项和为

因此级数的和

于是，余项的绝对值

由于级数的和 s(x)s(x)s(x) 趋于无穷大，所以在区间 [0,+∞)[0, +\infty)[0,+∞) 上不一致收敛。

例3

研究例1中的级数 在区间 (0,1)(0, 1)(0,1) 内的一致收敛性。

解答：

二、魏尔斯特拉斯(Weierstrass)判别法

以上两例都是直接根据定义来判定级数的一致收敛性的，现在介绍一个在实用上较方便的判别法。

定理（魏尔斯特拉斯判别法）

证明：

由条件（2），对任意给定的 ϵ>0\epsilon > 0ϵ>0，根据柯西审敛原理（第一节第三目）存在正整数 NNN，使得当 n>Nn > Nn>N 时，对任意的正整数 ppp，都有

由条件（1），对任何 x∈Ix \in Ix∈I，都有

令 p→∞p \to \inftyp→∞，则由上式得

因此函数项级数 ∑un(x)\sum u_n(x)∑un​(x) 在区间 III 上一致收敛。

解答：

因为在 (−∞,+∞)(- \infty, + \infty)(−∞,+∞) 内

而

收敛，故由魏尔斯特拉斯判别法，所给级数在 (−∞,+∞)(- \infty, + \infty)(−∞,+∞) 内一致收敛。

学习收获

通过这些例子和定理，我们不仅掌握了函数项级数一致收敛性的定义和判别方法，还理解了一致收敛性在函数分析中的重要性。这些知识在进一步研究函数项级数的性质及其应用中具有重要的意义。希望通过这些内容的学习，能够帮助大家更好地理解和掌握函数项级数的一致收敛性及其基本性质。

二、一致收敛级数的基本性质

一致收敛级数有如下基本性质：

定理 1

如果级数的各项 un(x)u_n(x)un​(x) 在区间 [a,b][a,b][a,b] 上都连续，且级数 ∑un(x)\sum u_n(x)∑un​(x) 在区间 [a,b][a,b][a,b] 上一致收敛于 s(x)s(x)s(x)，那么 s(x)s(x)s(x) 在 [a,b][a,b][a,b] 上也是连续的。

证明：

得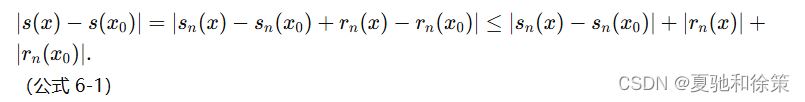

因为级数一致收敛于 s(x)s(x)s(x)，所以对任意给定的正数 ϵ\epsilonϵ，必有正整数 N=N(ϵ)N = N(\epsilon)N=N(ϵ)，使得当 n>Nn > Nn>N 时，对 [a,b][a,b][a,b] 上的一切 xxx，都有 ∣rn(x)∣<ϵ3,|r_n(x)| < \frac{\epsilon}{3},∣rn​(x)∣<3ϵ​, （公式 6-2）

当然，也有 ∣rn(x0)∣<ϵ3.|r_n(x_0)| < \frac{\epsilon}{3}.∣rn​(x0​)∣<3ϵ​.

选定满足 n>Nn > Nn>N 的 nnn 之后，sn(x)s_n(x)sn​(x) 是有限项连续函数之和，故 sn(x)s_n(x)sn​(x) 在点 x0x_0x0​ 连续，从而必有一个 δ>0\delta > 0δ>0 存在，当 ∣x−x0∣<δ|x - x_0| < \delta∣x−x0​∣<δ 时，总有

由（公式 6-1）、（公式 6-2）、（公式 6-3）可见，对任给 ϵ>0\epsilon > 0ϵ>0，必有 δ>0\delta > 0δ>0，当 ∣x−x0∣<δ|x - x_0| < \delta∣x−x0​∣<δ 时，有

所以 s(x)s(x)s(x) 在点 x0x_0x0​ 处连续，而 x0x_0x0​ 在 [a,b][a,b][a,b] 上是任意的，因此 s(x)s(x)s(x) 在 [a,b][a,b][a,b] 上连续。

定理 2

如果级数 ∑un(x)\sum u_n(x)∑un​(x) 的各项 un(x)u_n(x)un​(x) 在区间 [a,b][a,b][a,b] 上连续，且 ∑un(x)\sum u_n(x)∑un​(x) 在 [a,b][a,b][a,b] 上一致收敛于 s(x)s(x)s(x)，那么级数可以逐项积分，即

其中 a≤x0<x≤ba \leq x_0 < x \leq ba≤x0​<x≤b，并且上式右端的级数在 [a,b][a,b][a,b] 上也一致收敛。

证明：

因为级数 ∑un(x)\sum u_n(x)∑un​(x) 在 [a,b][a,b][a,b] 上一致收敛，由定理 1，s(x)s(x)s(x) 和 un(x)u_n(x)un​(x) 都在 [a,b][a,b][a,b] 上连续，所以积分存在，从而有

又由级数的一致收敛性，对任给正数 ϵ\epsilonϵ，必有 N=N(ϵ)N = N(\epsilon)N=N(ϵ)，使得当 n>Nn > Nn>N 时，对 [a,b][a,b][a,b] 上的一切 xxx，都有

于是，当 n>Nn > Nn>N 时有

根据极限的定义，有 ∫ 即

由于 NNN 只依赖于 ϵ\epsilonϵ 而与 x0,xx_0, xx0​,x 无关，所以级数在 [a,b][a,b][a,b] 上一致收敛。

定理 3

如果级数 ∑un(x)\sum u_n(x)∑un​(x) 在区间 [a,b][a,b][a,b] 上收敛于和 s(x)s(x)s(x)，它的各项 un(x)u_n(x)un​(x) 都具有连续导数 un′(x)u_n'(x)un′​(x)，并且级数 ∑un′(x)\sum u_n'(x)∑un′​(x) 在 [a,b][a,b][a,b] 上一致收敛，那么级数在 [a,b][a,b][a,b] 上也一致收敛，且可逐项求导，即

证明：

欲证（公式 6-5），只需证

根据定理 1，ϕ(x)\phi(x)ϕ(x) 在 [a,b][a,b][a,b] 上连续，根据定理 2，级数 ∑un(x)\sum u_n(x)∑un​(x) 可逐项积分，故有

而

从而有

上式两端求导，即得关系式

再证级数 ∑un′(x)\sum u_n'(x)∑un′​(x) 在 [a,b][a,b][a,b] 上也一致收敛。根据定理 2，级数

所以

由此即得所要证的结论。

注意：

级数一致收敛并不能保证可以逐项求导。例如，在例4中我们已证明了级数

在任何区间 [a,b][a,b][a,b] 上都是一致收敛的，但逐项求导后的级数

其一般项不趋于零，所以对任意值 xxx 都是发散的，因此原级数不可以逐项求导。下面我们来讨论幂级数的一致收敛性。

定理 4

如果幂级数的收敛半径为 R>0R > 0R>0，那么此级数在 (−R,R)(-R, R)(−R,R) 内的任一闭区间 [a,b][a,b][a,b] 上一致收敛。

证明：

而 0<r<R0 < r < R0<r<R。根据第三节定理 1 级数绝对收敛，由魏尔斯特拉斯判别法即得所要证的结论。

进一步还可证明，如果幂级数在收敛区间的端点收敛，那么一致收敛的区间可扩大到包含端点。

下面我们来证明在第三节中指出的关于幂级数在其收敛区间内的和函数的连续性、逐项可导、逐项可积的结论。

关于和函数的连续性及逐项可积的结论，由定理 4 和定理 1、定理 2 立即可得。关于逐项可导的结论，我们重新叙述成如下定理并给出证明。

定理 5

如果幂级数的收敛半径为 R>0R > 0R>0，那么其和函数 s(x)s(x)s(x) 在 (−R,R)(-R, R)(−R,R) 内可导，且有逐项求导公式

逐项求导后所得到的幂级数与原级数有相同的收敛半径。

证明：

先证级数 内收敛。

在 (−R,R)(-R, R)(−R,R) 内任意取定 xxx，再选定 x1x_1x1​，使得 ∣x∣<x1<R|x| < x_1 < R∣x∣<x1​<R。记 q=∣x∣x1<1q = \frac{|x|}{x_1} < 1q=x1​∣x∣​<1，则

由比值审敛法可知级数 收敛，于是

故数列 ∣nanxn−1∣|n a_n x^{n-1}|∣nan​xn−1∣ 有界，必有 M>0M > 0M>0，使得

又由于 0<x1<R0 < x_1 < R0<x1​<R，级数 ∑nanx1n−1qn−1\sum n a_n x_1^{n-1} q^{n-1}∑nan​x1n−1​qn−1 收敛，由比较审敛法的推论即得级数 ∑nanxn−1\sum n a_n x^{n-1}∑nan​xn−1 收敛。

由定理 4，级数 ∑nanxn−1\sum n a_n x^{n-1}∑nan​xn−1 在 [−R,R][-R, R][−R,R] 内的任一闭区间 [a,b][a, b][a,b] 上一致收敛，故幂级数在 [a,b][a, b][a,b] 上适合定理 3 的条件，从而可逐项求导。再由 [a,b][a, b][a,b] 在 (−R,R)(-R, R)(−R,R) 内的任意性，即得幂级数在 (−R,R)(-R, R)(−R,R) 内可逐项求导。

设幂级数的收敛半径为 R′R'R′，上面已证得 R≤R′R \leq R'R≤R′。将此幂级数在 [0,x][0, x][0,x]（∣x∣<R′|x| < R'∣x∣<R′）上逐项积分即得，由逐项积分所得级数的收敛半径不会缩小，所以 R′≤RR' \leq RR′≤R，于是 R′=RR' = RR′=R。

定理 5 证毕。