【数学推导】空间中一点绕任意轴旋转

最新推荐文章于 2023-04-12 21:42:55 发布

Lwang2018

最新推荐文章于 2023-04-12 21:42:55 发布

阅读量1.1k

点赞数

分类专栏： math 文章标签：矩阵

本文链接：https://blog.csdn.net/thunder_k/article/details/129004648

版权

math 专栏收录该内容

1 篇文章

订阅专栏

该代码实现了一个函数，用于在三维空间中计算点绕任意轴的旋转。它涉及向量平移、旋转和平移回原点的过程，利用矩阵运算来完成。公式和步骤详细解释了如何构建旋转矩阵，并最终得到新的位置坐标。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

绕任意轴旋转的情况比较复杂，可按如下方法处理：

将旋转轴平移至原点
将旋转轴旋转至YOZ平面
将旋转轴旋转至于Z轴重合
绕Z轴旋转θ度
执行步骤3的逆过程
执行步骤2的逆过程
执行步骤1的逆过程

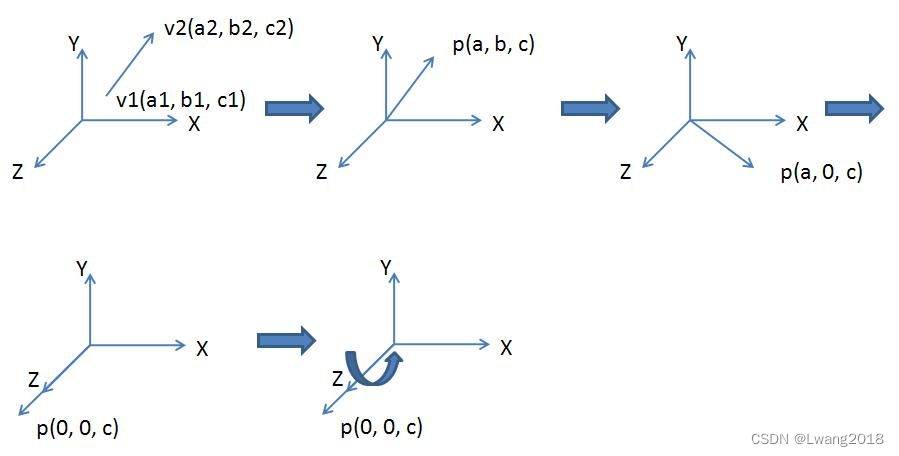
假设用v1(a1, b2, c2)和v2(a2, b2, c2)来表示旋转轴，θ表示旋转角度。为了方便推导，暂时使用右手系并使用列向量，待得出矩阵后转置一下即可，上面步骤对应的流程图如下：
在这里插入图片描述

CVector3D RandomRotate(CVector3D p, CVector3D a0, CVector3D a1, float theta)
{
	CVector3D newPosition;
	CVector3D b = a1 - a0;
	b.Normalize();

	theta = theta * PI / 180;

	float u = b.x;
	float v = b.y;
	float w = b.z;

	float SinA = sin(theta);
	float CosA = cos(theta);

	float uu = u * u;
	float vv = v * v;
	float ww = w * w;
	float uv = u * v;
	float uw = u * w;
	float vw = v * w;

	float t00 = uu + (vv + ww) * CosA;
	float t10 = uv * (1 - CosA) + w * SinA;
	float t20 = uw * (1 - CosA) - v * SinA;
	float t30 = 0;

	float t01 = uv * (1 - CosA) - w * SinA;
	float t11 = vv + (uu + ww) * CosA;
	float t21 = vw * (1 - CosA) + u * SinA;
	float t31 = 0;

	float t02 = uw * (1 - CosA) + v * SinA;
	float t12 = vw * (1 - CosA) - u * SinA;
	float t22 = ww + (uu + vv) * CosA;
	float t32 = 0;

	float t03 = (a1.x * (vv + ww) - u * (a1.y * v + a1.z * w)) * (1 - CosA) + (a1.y * w - a1.z * v) * SinA;
	float t13 = (a1.y * (uu + ww) - v * (a1.x * u + a1.z * w)) * (1 - CosA) + (a1.z * u - a1.x * w) * SinA;
	float t23 = (a1.z * (uu + vv) - w * (a1.x * u + a1.y * v)) * (1 - CosA) + (a1.x * v - a1.y * u) * SinA;
	float t33 = 1;

	newPosition.x = (float)(t00 * p.x + t01 * p.y + t02 * p.z + t03);
	newPosition.y = (float)(t10 * p.x + t11 * p.y + t12 * p.z + t13);
	newPosition.z = (float)(t20 * p.x + t21 * p.y + t22 * p.z + t23);

	return newPosition;
}

参考 https://www.cnblogs.com/graphics/archive/2012/08/10/2627458.html