* 引子 数学相关的东西,随便记记 :)~
对于矩阵,OpenGL采用列主序(column-major order)存储,之前对于这个概念有些模糊,后来又了解了一些相关知识,在此一记~
首先是数学概念上的矩阵,这是根据标准定义的,譬如一个4*4的矩阵,可表示为:
而采用列主序存储,则可以理解为一种矩阵在计算机中的实现方式,或者更确切的说,是存储方式,即虽然在数学上明确定义了矩阵的表示方式,但是在计算机中怎么实现(或者说存储)则是另一个问题,列主序存储就是这个问题的一种解决方法~(感觉颇像Unicode和UTF-8的关系:))
而所谓列主序的方式,就是以矩阵列为优先来存储矩阵元素,拿C/C++中的数组举例,如果要存储上述的4*4矩阵,那么内存中的布局应该是这个样子的~
更具体的例子可以参考Cocos2d-x中的Mat4类(来自于GamePlay3D),譬如矩阵变换(列)向量:
inline void MathUtilC::transformVec4(const float* m, const float* v, float* dst)
{
// Handle case where v == dst.
float x = v[0] * m[0] + v[1] * m[4] + v[2] * m[8] + v[3] * m[12];
float y = v[0] * m[1] + v[1] * m[5] + v[2] * m[9] + v[3] * m[13];
float z = v[0] * m[2] + v[1] * m[6] + v[2] * m[10] + v[3] * m[14];
float w = v[0] * m[3] + v[1] * m[7] + v[2] * m[11] + v[3] * m[15];
dst[0] = x;
dst[1] = y;
dst[2] = z;
dst[3] = w;
}拿上面 x 的计算来说,其所取的矩阵元素索引分别为0,4,8,12,正是m11,m12,m13以及m14 ~
That's it ~








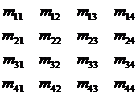















 8226
8226

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








