基于物理的渲染理论基础（PBR渲染）

基于物理的渲染，通俗一点说就是根据现实环境上光是如何照到物体，然后物体如何把光的颜色反射到人的眼睛的过程，通过渲染表达出来。而游戏中基于物理的渲染就是通过数学公式建模的方式来模拟（只是模拟并非完全准确）这个过程，从而达到更接近现实世界的渲染效果，显得画面更逼真。

从上面这句话的描述得知，整个物理渲染其实就用一句话最简单的话总结就是：、
求光从某个方向照射到物体后反射出来到肉眼的光。
用更具学术性的话语说就是：
求物体的双向反射分布函数，即BRDF。

因此，要在渲染上实现上面这句话，就要求我们去解开这些问题：
1、光是什么，如何用数学来量化光照。
2、物体会对光进行怎么样的反射，如何用数学来对此进行建模。
3、求出光经过物体反射后得到的光值是多少。

基于物理渲染的数学理论（推荐）

光是什么

光是一种电磁横波，以上下震荡的方式直线传播，电磁波的覆盖范围很广，但只有很小的一部分范围内（大约400到700纳米）对人类是可见的，因此着色只需要关注这部分。眼睛对光电磁波的不同频率感应为不同的颜色。

如何量化光

要对光进行数学量化，而光传播的本质是以电磁波辐射能量进行传播的，而辐射学(Radiometry)是用来度量电磁波辐射的学科，因此可以用辐射学来量化光的传播。

辐射学的常见基本量：

量化值	符号	单位	定义
辐射能量 (Radiant Energy)	$Q$	$J$	表面上入射的能量
辐射通量 (Radiant Flux)	$\Phi$	$W$或$J/s$	表面上入射能量的功率
辐照度（Irradiance）	$E$	$W/{\mathbf{m}}^2$	单位面积上的能量入射功率
辐射度（Radiosity）	$J$	$W/{\mathbf{m}}^2$	单位面积上的能量出射功率
辐射强度（Intensity）	$I$	$W/{\mathbf{s}\mathbf{r}}^2$	单位立体角的辐射通量
辐射率（Radiance）	$L$	$W/({\mathbf{m}}^2\mathbf{s}\mathbf{r}{)}^2$	每单位面积每单位立体角的辐射通量

什么是立体角：

立体角其实就是2D圆的弧度角扩展到3D空间的表示，如上图中${\mathbf{r}}^2$即为半径为$\mathbf{r}$的球的立体角，这里辐射学用的通常是单位球。用$\omega$表示立体角，单位为$sr$(stereo radian)。(也有不规则的立体角，辐射学这里关注的是在单位球上形成圆边的曲面立体角)。

各个辐射学术名的关系与特点：

1、能量

能量用焦耳($J$)衡量，光源散射光子，每个光子具有特定的波长,对应的波长携带特定的能量。所有的基本辐射量实际上都是用不同的方法对光子进行测量。一个光子在波长为$\lambda$时携带的能量：
$$Q=\frac{hc}{\lambda }$$
$c$：光速，即$299,472,458\mathbf{m}/\mathbf{s}$。
$h$：普朗克常量，$h\approx 6.626\times 10^{-34}{\mathbf{m}}^2\mathbf{k}\mathbf{g}/\mathbf{s}$。

2、辐射通量：

$$\Phi =\frac{Q}{t}$$
$d$：微分表示符。
$t$：时间。

3、辐照度：

对于点光源，$E$有公式：
$$E=\frac{\Phi }{4\pi r^2}$$

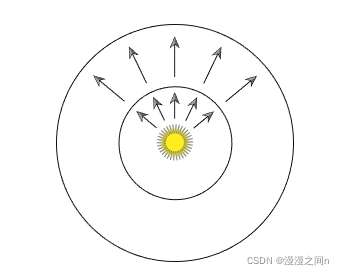
图解：辐射通量用于测量空间上通过的能量，对于点光源，能量会随着距离的增加而递减，但总的能量保持不变。

对于平行光，$E$有公式：
$$E=\frac{\Phi }{A}$$
$A$：面积。

定义垂直入射光方向的辐照度：
$$E{}_{\perp }=$$