3.9 训练一个 Softmax 分类器-深度学习第二课《改善深层神经网络》-Stanford吴恩达教授

---

←上一篇	↓↑	下一篇→
3.8 Softmax 回归	回到目录	3.10 深度学习框架

---

训练一个 Softmax 分类器 (Training a Softmax Classifier)

上一个视频中我们学习了Softmax层和Softmax激活函数，在这个视频中，你将更深入地了解Softmax分类，并学习如何训练一个使用了Softmax层的模型。

回忆一下我们之前举的的例子，输出层计算出的 $z^{[l]}$ 如下， $z^{[l]}=\left[\begin{array}{c}5\\ 2\\ -1\\ 3\end{array}\right]$ 我们有四个分类 $C=4$ ， $z^{[l]}$ 可以是4×1维向量，我们计算了临时变量 $t$ ， $t=\left[\begin{array}{c}{e}^5\\ e^2\\ e^{-1}\\ e^3\end{array}\right]$ ，对元素进行幂运算，最后，如果你的输出层的激活函数 $g^{(L)}()$ 是Softmax激活函数，那么输出就会是这样的：

简单来说就是用临时变量 $t$ 将它归一化，使总和为1，于是这就变成了 $a^{[L]}$ ，你注意到向量 $z$ 中，最大的元素是5，而最大的概率也就是第一种概率。

Softmax这个名称的来源是与所谓hardmax对比，hardmax会把向量 $z$ 变成这个向量 $\left[\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right]$ ，hardmax函数会观察 $z$ 的元素，然后在 $z$ 中最大元素的位置放上1，其它位置放上0，所这是一个hard max，也就是最大的元素的输出为1，其它的输出都为0。与之相反，Softmax所做的从 $z$ 到这些概率的映射更为温和，我不知道这是不是一个好名字，但至少这就是softmax这一名称背后所包含的想法，与hardmax正好相反。

有一点我没有细讲，但之前已经提到过的，就是Softmax回归或Softmax激活函数将logistic激活函数推广到 $C$ 类，而不仅仅是两类，结果就是如果 $C=2$ ，那么 $C=2$ 的Softmax实际上变回了logistic回归，我不会在这个视频中给出证明，但是大致的证明思路是这样的，如果 $C=2$ ，并且你应用了Softmax，那么输出层 $a^{[L]}$ 将会输出两个数字，如果 $C=2$ 的话，也许输出0.842和0.158，对吧？这两个数字加起来要等于1，因为它们的和必须为1，其实它们是冗余的，也许你不需要计算两个，而只需要计算其中一个，结果就是你最终计算那个数字的方式又回到了logistic回归计算单个输出的方式。这算不上是一个证明，但我们可以从中得出结论，Softmax回归将logistic回归推广到了两种分类以上。

接下来我们来看怎样训练带有Softmax输出层的神经网络，具体而言，我们先定义训练神经网络使会用到的损失函数。举个例子，我们来看看训练集中某个样本的目标输出，真实标签是 $\left[\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right]$ ，用上一个视频中讲到过的例子，这表示这是一张猫的图片，因为它属于类1，现在我们假设你的神经网络输出的是 $\hat{y}$ ， $\hat{y}$ 是一个包括总和为1的概率的向量， $y=\left[\begin{array}{c}0.3\\ 0.2\\ 0.1\\ 0.4\end{array}\right]$ ，你可以看到总和为1，这就是 $a^{[l]}$ ， $a^{[l]}=y=\left[\begin{array}{c}0.3\\ 0.2\\ 0.1\\ 0.4\end{array}\right]$ 。对于这个样本神经网络的表现不佳，这实际上是一只猫，但却只分配到20%是猫的概率，所以在本例中表现不佳。

那么你想用什么损失函数来训练这个神经网络？在Softmax分类中，我们一般用到的损失函数是 $L(\hat{y},y)=-{\sum }_{j=1}^4{y}_j\log {\hat{y}}_j$ ，我们来看上面的单个样本来更好地理解整个过程。注意在这个样本中 $y_1=y_3=y_4=0$ ，因为这些都是0，只有 $y_2=1$ ，如果你看这个求和，所有含有值为0的 $y_j$ 的项都等于0，最后只剩下 $-y_{2}t\log {\hat{y}}_2$ ，因为当你按照下标 $j$ 全部加起来，所有的项都为0，除了 $j=2$ 时，又因为 $y_2=1$ ，所以它就等于 $-\log {\hat{y}}_2$ 。 $L(\hat{y},y)=-{\sum }_{j=1}^4{y}_j\log {\hat{y}}_j=-y_2\log {\hat{y}}_2=-\log {\hat{y}}_2$

这就意味着，如果你的学习算法试图将它变小，因为梯度下降法是用来减少训练集的损失的，要使它变小的唯一方式就是使 $-\log {\hat{y}}_2$ 变小，要想做到这一点，就需要使 ${\hat{y}}_2$ 尽可能大，因为这些是概率，所以不可能比1大，但这的确也讲得通，因为在这个例子 $x$ 中是猫的图片，你就需要这项输出的概率尽可能地大（ $y=\left[\begin{array}{c}0.3\\ 0.2\\ 0.1\\ 0.4\end{array}\right]$ 中第二个元素）。

概括来讲，损失函数所做的就是它找到你的训练集中的真实类别，然后试图使该类别相应的概率尽可能地高，如果你熟悉统计学中最大似然估计，这其实就是最大似然估计的一种形式。但如果你不知道那是什么意思，也不用担心，用我们刚刚讲过的算法思维也足够了。

这是单个训练样本的损失，整个训练集的损失 $J$ 又如何呢？也就是设定参数的代价之类的，还有各种形式的偏差的代价，它的定义你大致也能猜到，就是整个训练集损失的总和，把你的训练算法对所有训练样本的预测都加起来， $J(w^{[1]},b^{[1]},\cdots )=\frac{1}{m}{\sum }_{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)})$

因此你要做的就是用梯度下降法，使这里的损失最小化。

最后还有一个实现细节，注意因为 $C=4$ ， $y$ 是一个4×1向量， $y$ 也是一个4×1向量，如果你实现向量化，矩阵大写 $Y$ 就是 $\left[\begin{array}{c}{y}^{(1)}{y}^{(2)}\cdots \cdots y^{(m)}\end{array}\right]$ ，例如如果上面这个样本是你的第一个训练样本，那么矩阵 $Y=\left[\begin{array}{cccc}0& 0& 1& \cdots \\ 1& 0& 0& \cdots \\ 0& 1& 0& \cdots \\ 0& 0& 0& \cdots \end{array}\right]$ ，那么这个矩阵 $Y$ 最终就是一个 $4\ast m$ 维矩阵。类似的， $\hat{Y}=\left[\begin{array}{c}{\hat{y}}^{(1)}{\hat{y}}^{(2)}\cdots \cdots {\hat{y}}^{(m)}\end{array}\right]$ ，这个其实就是 ${\hat{y}}^{(1)}（a^{[l](1)}=y^{(1)}=\left[\begin{array}{c}0.3\\ 0.2\\ 0.1\\ 0.4\end{array}\right]）$ ，或是第一个训练样本的输出，那么 $\hat{Y}=\left[\begin{array}{cc}0.3& \cdots \\ 0.2& \cdots \\ 0.1& \cdots \\ 0.4& \cdots \end{array}\right]$ ， $\hat{Y}$ 本身也是一个 $4\ast m$ 维矩阵。

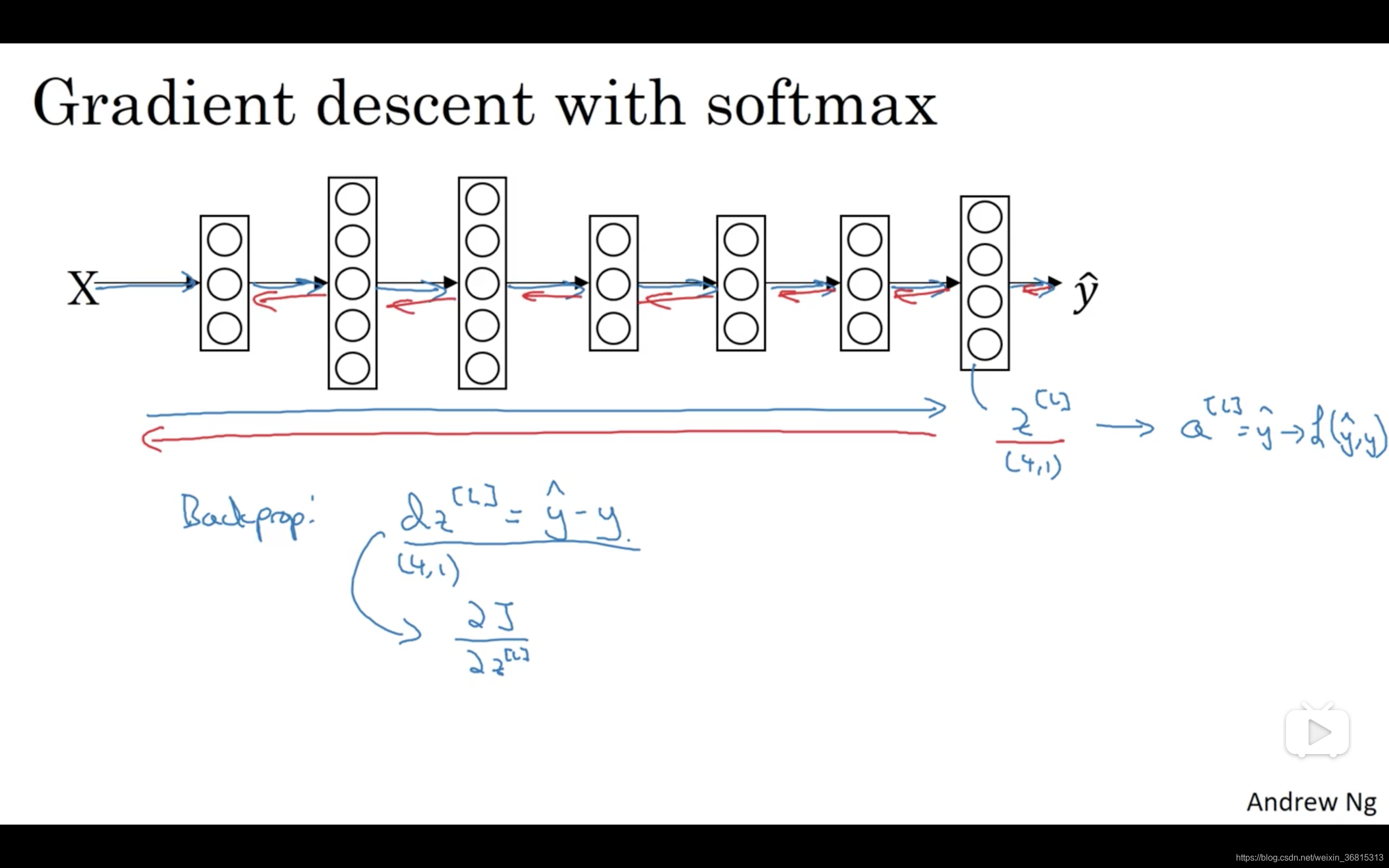
最后我们来看一下，在有Softmax输出层时如何实现梯度下降法，这个输出层会计算 $z^{[l]}$ ，它是 $C\ast 1$ 维的，在这个例子中是4×1，然后你用Softmax激活函数来得到 $a^{[l]}$ 或者说 $y$ ，然后又能由此计算出损失。我们已经讲了如何实现神经网络前向传播的步骤，来得到这些输出，并计算损失，那么反向传播步骤或者梯度下降法又如何呢？其实初始化反向传播所需要的关键步骤或者说关键方程是这个表达式 $d{z}^{[l]}=\hat{y}-y$ ，你可以用 $\hat{y}$ 这个4×1向量减去 $y$ 这个4×1向量，你可以看到这些都会是4×1向量，当你有4个分类时，在一般情况下就是 $C\ast 1$ ，这符合我们对 $dz$ 的一般定义，这是对 $z^{[l]}$ 损失函数的偏导数（ $d{z}^{[l]}=\frac{\partial J}{\partial z^{[l]}}$ ），如果你精通微积分就可以自己推导，或者说如果你精通微积分，可以试着自己推导，但如果你需要从零开始使用这个公式，它也一样有用。

有了这个，你就可以计算 $d{z}^{[l]}$ ，然后开始反向传播的过程，计算整个神经网络中所需要的所有导数。

但在这周的初级练习中，我们将开始使用一种深度学习编程框架，对于这些编程框架，通常你只需要专注于把前向传播做对，只要你将它指明为编程框架，前向传播，它自己会弄明白怎样反向传播，会帮你实现反向传播，所以这个表达式值得牢记（ $d{z}^{[l]}=\hat{y}-y$ ），如果你需要从头开始，实现Softmax回归或者Softmax分类，但其实在这周的初级练习中你不会用到它，因为编程框架会帮你搞定导数计算。

Softmax分类就讲到这里，有了它，你就可以运用学习算法将输入分成不止两类，而是 $C$ 个不同类别。接下来我想向你展示一些深度学习编程框架，可以让你在实现深度学习算法时更加高效，让我们在下一个视频中一起讨论。

课程PPT

---

←上一篇	↓↑	下一篇→
3.8 Softmax 回归	回到目录	3.10 深度学习框架

---