矩阵求导法则的总结

最新推荐文章于 2024-05-25 22:00:57 发布
最新推荐文章于 2024-05-25 22:00:57 发布
阅读量6.2k 收藏 10
点赞数 2
分类专栏： 数学基础 文章标签： 矩阵求导总结
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_38133509/article/details/89737243
版权

最重要的写在前面：

进行更新：随着理解的加深，我发现之前写的有些问题，重新写一下吧

矩阵求导要分成两类，第一类是用在向量函数f(x)里，比如要在x0处展开，所以需要计算该点处的雅可比这些；第二类是为了计算统一，我们规定的分子布局或分母布局这样。

一、向量函数求导

形如y=f(x)这样的函数，如果考虑在x0处的展开就变成了

y=f(x_0) +J^T(x-x_0)+\frac{1}{2}(x-x_0)^TG(x-x_0)

其中y可能是一个值（scale），也可能是一个向量，分情况讨论下：

（1）值y_{1\times 1}对向量\mathbf{x}_{n\times1}求导

\frac{\partial y}{\partial \mathbf{x}}：这时也叫梯度，求导的结果的维度当然要和分母的向量保持一致，（类似分母布局）

（2）列向量\mathbf{y}_{m\times 1}对列向量\mathbf{x}_{n\times1}求导

\frac{\partial \mathbf{y}}{\partial \mathbf{x}}：这时也叫雅可比，先将y按列展开，再将x按行展开，所以得到的结果维度为mxn，（类似分子布局），

（3）还有hessian就不说了

 

二、矩阵之间的求导

这是需要考虑分子布局或分母布局，为了保持计算一致，我们需要选择一个规矩来计算，否则就乱了，不过我常见的还是分母布局；这时参考cook book就好，简单点就是说

\frac{\partial Ax}{\partial x^T} = A

\frac{\partial A^T x}{x} = A

这类的

 

三、小结

在算出来jacobian之后，后面的矩阵计算还是得按照分母布局来推，比如下面：

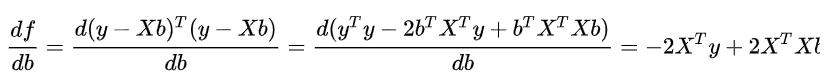
当然其实其实雅可比也是可以写成分母布局的，这样就得对应行向量了，因为雅可比后面跟着的是自变量x_nx1，所以还是要看自己的习惯，用哪个布局就选好配套的公式，不要一会这样一会那样，说到底都是为了计算方便，不管中间过程写成什么维度，可以算出正确结果就好了啊，只不过我是想按照这样的规律，以防自己算错

 

Reference：

https://blog.csdn.net/daaikuaichuan/article/details/80620518--------详细讲了我上面提到的几个例子,建议结合着看☆

https://blog.csdn.net/lipengcn/article/details/52815429 ---------------有很多公式的，虽然有的也不一定对

https://blog.csdn.net/nomadlx53/article/details/50849941-------------讲分母布局和分子布局的

http://www.pianshen.com/article/5516168061/ --------------------------分子分母布局的对比

https://www.jianshu.com/p/4128e5b31fb4---------------------------------分母布局讲的比较细

bh_宫商角徵羽
关注
  • 2
    点赞
  • 踩
  • 10
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
矩阵求导公式的简单总结
05-31
矩阵求导公式的总结，感觉还不错。当然，是网上的资源
矩阵的求导
weixin_39910711的博客
08-13 3万+
目录 1布局(Layout) 1.1矩阵向量求导引入 1.2矩阵向量求导定义 1.3矩阵向量求导布局 1.4 分母布局的另一种求解方法 1.5 总结 2基本的求导规则 2.1向量对标量求导（相对于数量变量的微分，即自变量是数量变量） 2.1.1 定义 2.1.2 运算法则 2.2标量y 对向量x求导（数量函数相对于向量的微分） 2.2.1 定义 2.2...
机器学习必备数学基础！-- 矩阵求导
最新发布
2301_82023330的博客
05-25 816
本文章主要介绍了矩阵微积分中的 矩阵求导 相关数学知识
矩阵求导公式总结
susandebug
06-12 8万+
今天推导公式，发现居然有对矩阵的求导，狂汗--完全不会。不过还好网上有人总结了。吼吼，赶紧搬过来收藏备份。 基本公式： Y = A * X --> DY/DX = A' Y = X * A --> DY/DX = A Y = A' * X * B --> DY/DX = A * B' Y = A' * X' * B --> DY/DX = B * A' 1. 矩阵Y对标量x求导
[机器学习-数学] 矩阵求导(分母布局与分子布局)，以及常用的矩阵求导公式
Harry的博客
07-09 1万+
0 矩阵求导(分布布局) 1，矩阵求导的本质 矩阵A对矩阵B求导： 矩阵A中的每一个元素分别对矩阵B中的每个元素进行求导。 一、矩阵求导 常见的矩阵求导方式有：向量对向量求导，标量对向量求导，向量对标量求导。 1、向量对向量求导 2、标量对向量求导 3、向量对标量求导 二、几种重要的矩阵 1、梯度（Gradient） 2、雅克比矩阵（Jacobian matrix） 3、海森矩阵（Hessian matrix） 三、常用的矩阵求导公式 参考资料 http://blog.sina.
矩阵求导法则与性质
热门推荐
crazy_scott的博客
07-04 9万+
介绍矩阵求导法则，以及常用的求导公式、迹函数、行列式求导结论 矩阵求导法则 矩阵求导应该分为标量求导、向量求导、矩阵求导三个方面来介绍，公式繁多，但仔细看看其实是有规律可循的。 标量求导 无论是矩阵、向量对标量求导，或者是标量对矩阵、向量求导，其结论都是一样的：等价于对矩阵（向量）的每个分量求导，并且保持维数不变。 例如，我们可以计算标量对向量求导： 设yyy为一个元素，x...
最基本矩阵求导公式
ningzian的博客
01-28 3043
文章目录1. 矩阵求导法则1.1 标量求导1.2 向量求导1.3矩阵求导 1. 矩阵求导法则 矩阵的求导分为：标量求导、向量求导、矩阵求导三个方面。 1.1 标量求导 矩阵和向量对标量求导，只需矩阵中的每个量都对标量进行求导，这个很好理解。 标量对矩阵的向量求导，也是同样的，等价于标量对矩阵的每个分量进行求导，并且保持维数不变。 举例。设yyy为一个标量，xT=[x1x2⋯xn]x^T=[x_...
矩阵 向量求导法则
04-05
机器学习数学基础，矩阵 向量求导法则必会
矩阵、向量求导法则
09-12
该文档总结了矩阵对矩阵、矩阵对向量、向量对矩阵、向量对向量、元素对矩阵、元素对向量的求导法则，非常有用！
矩阵向量求导法则两篇
11-22
矩阵、向量求导法则 中文版 包含所有情况和公式，适合翻阅查找 英文版包含推导，非常详细，适合精度，包含了矩阵tr技巧
矩阵、向量求导法则1
08-04
1. 行向量对元素求导 2. 列向量对元素求导 3. 矩阵对元素求导 4. 元素对行向量求导 5. 元素对列向量求导 6. 元素对矩阵求导 7. 行向量对列向量
矩阵求导1
08-03
《矩阵求导基础》 矩阵求导是多元函数求导的一种表达方式，它将复杂的多元函数求导问题简化为矩阵的形式，便于理解和计算。在机器学习领域，矩阵和向量的求导规则尤为重要，因为它们构成了许多算法的基础，如梯度...
矩阵求导
清风拂面
12-04 5328
一、矩阵和向量求导 机器学习中最常用的矩阵求导有：标量对矩阵的求导，矩阵对标量求导以及向量对向量的求导。下面分别对这几种求导方式进行介绍。 标量对矩阵的求导 如果函数f把一个元素为实数的m×n矩阵，映射为一个实数，则 也就是实值函数f对矩阵X求导其实就是f对X的各元素分别求导得到一个与X同型的矩阵。比如 且f(X)=x + 2y + 3z + 4w，则 再比如正规方程推导那篇文章中的例子，设 ，则 矩阵对标量的求导 如果函数f把实数x映射成一个元素为实数的m×n矩阵 也就是矩阵Y
关于矩阵求导的理解与计算方法
刘之帅
03-10 4229
前言 我今年大四即将毕业，毕设是深度学习相关，在进行理论学习时，一度对矩阵微分感到困惑，本科学习期间没接触过这个（软件工程专业。。。），网上资料也很零散，在《神经网络与深度学习》的数学基础篇章有相对详细的介绍(但是也少的可怜)，下面是东拼西凑又求朋问友得到的个人理解，因为本人接触深度学习较晚，又非数学专业，所以可能有理解错误的地方，希望能和大家讨论。 文章目录前言矩阵微分矩阵与标量、标量与矩阵标量...
矩阵求导公式
Justpayne的专栏
01-20 4941
基本公式： Y = A * X --> DY/DX = A' Y = X * A --> DY/DX = A Y = A' * X * B --> DY/DX = A * B' Y = A' * X' * B --> DY/DX = B * A' 1. 矩阵Y对标量x求导： 相当于每个元素求导数后转置一下，注意M×N矩阵求导后变成N×M了 Y = [y(ij)] -->
【矩阵论】3. 矩阵函数——矩阵函数求导
努力，奋斗！
11-22 5085
矩阵函数求导： 积分与求导定义；含参阵求导，3个含参阵求导， 一阶线性常系数微分方程组求解
【机器学习中的矩阵求导】（五）矩阵对矩阵求导
发现问题，并解决问题，批判性思维
11-30 5238
学习总结 （1）这个task所有求导布局都是分母布局。为了适配矩阵对矩阵的求导，这次的向量对向量的求导，也是以分母布局为准（和之前的不一样）。 （2）由于矩阵对矩阵求导的结果包含【克罗内克积】，因此和之前我们讲到的其他类型的矩阵求导很不同，在机器学习算法优化中中，我们一般不在推导的时候使用矩阵对矩阵的求导，除非只是做定性的分析。如果遇到矩阵对矩阵的求导不好绕过，一般可以使用机器学习中的矩阵向量求导(四) 矩阵向量求导链式法则中第三节最后的几个链式法则公式来避免。 文章目录学习总结一、矩阵对矩阵求导的定义1.
矩阵求导（转）
weixin_30881367的博客
09-14 1074
在网上看到有人贴了如下求导公式： Y = A * X --> DY/DX = A' Y = X * A --> DY/DX = A Y = A' * X * B --> DY/DX = A * B' Y = A' * X' * B --> DY/DX = B * A' 于是把以前学过的矩阵求导部分整理一下： 1. 矩阵Y对标量x求导： 相当于每个元...
矩阵求导与转置运算
牧码杭城
10-20 1万+
线性代数补充矩阵转置矩阵求导 前言：在推导算法过程中遇到一些数学运算，遇到了就记录下，方便回忆 矩阵转置 (A+B)T=AT+BT(AB)T=BTAT (A+B)^T = A^T+B^T \\ (AB)^T = B^TA^T (A+B)T=AT+BT(AB)T=BTAT 矩阵求导 ∂Ax∂x=AT∂Ax∂xT=A∂xTA∂x=A \frac{\partial Ax}{\partial x} =...
复合函数的矩阵求导法则
10-15
复合函数的矩阵求导法则是链式法则的一种推广，它适用于多元函数的情况。设 $y=f(u)$，$u=g(x)$，则 $y=f(g(x))$，根据链式法则，有： $$\frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}$$ 将 $y=f(u)$ 和 $u=g(x)$ 带入上式，得到： $$\frac{dy}{dx}=\frac{df}{du}\cdot\frac{dg}{dx}$$ 其中，$\frac{df}{du}$ 表示 $f(u)$ 对 $u$ 的导数，$\frac{dg}{dx}$ 表示 $g(x)$ 对 $x$ 的导数。 对于多元函数 $y=f(u_1,u_2,\cdots,u_m)$，$u_i=g_i(x_1,x_2,\cdots,x_n)$，则有： $$\frac{\partial y}{\partial x_j}=\sum_{i=1}^m\frac{\partial y}{\partial u_i}\cdot\frac{\partial u_i}{\partial x_j}$$ 其中，$\frac{\partial y}{\partial u_i}$ 表示 $y$ 对 $u_i$ 的偏导数，$\frac{\partial u_i}{\partial x_j}$ 表示 $u_i$ 对 $x_j$ 的偏导数。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值