机器人动力学与控制学习笔记（十）————自适应控制（模型参考自适应控制）

最新推荐文章于 2024-04-05 20:59:03 发布

Kocurry

最新推荐文章于 2024-04-05 20:59:03 发布

阅读量2.2w

点赞数 37

分类专栏：机器人学

本文链接：https://blog.csdn.net/weixin_38452841/article/details/109176093

版权

机器人学专栏收录该内容

20 篇文章 244 订阅

订阅专栏

一、模型参考自适应

模型参考自适应是比较流行的自适应控制方式之一。模型参考自适应控制系统的设计主要有两大类方法：一种是基于局部参数最优化的设计方法；另一种是基于稳定性理论的设计方法，包括以下两种具体的设计方法：

基于Lyapunov稳定性理论的方法；
基于Popov超稳定性理论和正实性概念的方法。

早期的自适应控制大多采用局部参数最优化的设计方法，其主要缺点是在整个自适应过程中难以保证闭环系统的全局稳定性。而基于稳定性理论的设计方法，则从保证系统稳定性的角度出发来选择自适应规律，因此易于保证系统的稳定性。

1.1 模型参考自适应控制系统的典型结构

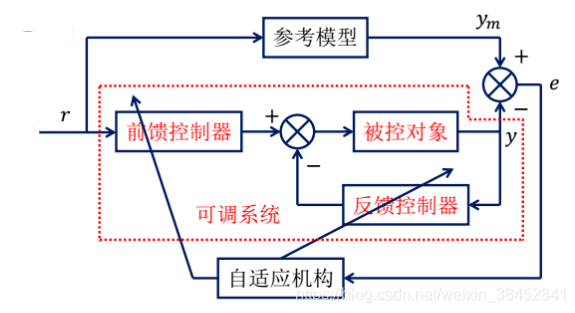
系统由参考模型、可调系统、自适应机构三部分构成。

可调系统包括被控对象、前置控制器和反馈控制器。
对可调系统的特性要求，如超调量、阻尼性能、过渡时间和通频带等由参考模型规定，故参考模型实际上是一种理想控制系统，其输出代表了期望的性能。
当参考模型与实际被控对象的输出有差异时，经比较器检测后，通过自适应机构做出决策，改变调节器（包括前置和反馈控制器）参数或生成辅助输入，以消除误差，使过程输出和参考模型输出一致。

参考模型与可调系统两者性能之间的一致性，由自适应机构保证，所以自适应机构的设计十分关键，性能一致性程度由状态广义误差向量

$e_{x}=x_{m}-x$

或输出误差向量

$e_{y}=y_{m}-y$

度量，其中 $x_{m},y_{m}$ 和 $x,y$ 分别为参考模型和可调系统的状态和输出。

只要误差向量不为零，自适应机构就按减少误差方向修正或更新控制律，以使系统实际性能指标达到或接近希望的性能指标。具体实施时，可更新前置和反馈控制器的参数，也可直接改变加到对象输入端的信号。前者称为参数自适应方案，后者称为信号综合自适应方案。

1.2 模型参考自适应控制系统的结构类型

注：在这三种结构中，并联型方案是最普遍的结构。尽管这三种结构的形式不同，但实际上对它们进行分析和综合的方法基本相同，故本节将限于讨论并联型模型参考自适应系统。

关于模型参考自适应控制系统的假定

参考模型是时不变系统；
参考模型和可调模型是线性的，有时为了分析方便，还假设它们的阶次相同；
广义误差可测；
在自适应控制过程中，可调参数或辅助信号仅依赖于自适应机构。

注：由于环境干扰引起的系统参数的变化相对于自适应调节速度要慢得多，故自适应速度快于对象参数的变化速度。假设4意味着自适应速度应大于被控对象参数的变化速度，否则就不可能实现渐进自适应。

1.3 基于局部参数最优化的设计方法（MIT方案）

局部参数最优化方法的设计思想：系统包含若干可调参数（如可调增益、反馈回路可调参数等），当被控对象的特性由于外界环境条件的改变或其他干扰的影响而发生变化时，自适应机构对这些可调参数进行调整，以补偿外界环境或其他干扰对系统性能的影响，从而逐步使得参考模型和控制对象之间的广义误差所构成的性能指标达到或接近最小值，因此它的设计原理就是构造一个由广义误差和可调参数组成的目标函数，并把它视为可调参数空间中的一个超曲面，利用参数最优化方法使这个目标函数逐渐减小，直到木目标函数达到最小或位于最小值的某个领域为止，从而满足可调系统与参考模型之间的一致性要求。

额外两条假设

可调系统参数已位于参考模型参数的某个邻域内；
相对于系统的内部动力学时间尺度而言，可调参数的调节速度低，即自适应增益小。

考虑具有一个可调增益的模型参考自适应控制系统，假设被控对象的传递函数为：

$W_{p}\left ( s \right )=\frac{N\left ( s \right )}{D\left ( s \right )}\cdot K_{p}$

其中， $D\left ( s \right )$ 和 $N\left ( s \right )$ 为已知的常系数多项式， $K_{ p}> 0$ 为对象的增益。

问题的背景

当系统受到干扰时，被控对象的增益 $K_{p}$ 可能发生变化，使其动态特性与参考模型的动态特性之间发生偏离， $K_{p}$ 的变化是不可测量的。为了克服由 $K_{p}$ 的漂移所造成的影响，在控制系统中设置一个可调增益 $K_{c}$ ，来补偿由 $K_{p}$ 的变化所造成的影响，期望使得 $K_{c}$ 与 $K_{p}$ 的乘积始终与模型的增益 $K_{m}$ 相一致。那么，如何设计自适应机构来实时地调整 $K_{c}$ ，即如何设计 $K_{c}$ 的自适应调整规律是需要解决的问题。

解决方法

构造理想参考模型的传递函数为：

$W_{m}\left ( s \right )=\frac{N\left ( s \right )}{D\left ( s \right )}\cdot K_{m}$

其中，增益 $K_{m}$ 是常数，认为是已知的，通常由期望的动态响应决定。

控制系统的结构图：

定义广义输出误差 $e$ 为：

$e=y_{m}-y$

其中， $y_{m}$ 为理想参考模型的输出； $y$ 为被控系统的输出； $e$ 表示输入信号为 $r\left ( t \right )$ 时，理想系统的响应与实际系统响应之间的偏离。

设计目标：确定可调增益 $K_{c}\left ( t \right )$ 的自适应调节律，使得下列性能指标 $J$ 达到最小

$J=\frac{1}{2}\int_{t_{0}}^{t}e^{2}\left ( \tau ,K_{c} \right )d\tau$ （1.1）

采用梯度法来寻求 $K_{c}\left ( t \right )$ 的最优调节律。

首先求 $J$ 对 $K_{c}$ 的偏导数有：

$\frac{\partial J }{\partial K_{c}}=\int_{t_{0}}^{t}e\frac{\partial e }{\partial K_{c}}d\tau$

根据梯度下降原理， $K_{c}$ 的变化量 $\Delta K_{c}$ 应正比于函数 $J$ 的负梯度方向，即取如下数值：

其中， $\eta > 0$ ，则调整后的 $K_{c}$ 为：

$K_{c}=\Delta K_{c}+K_{c0}=-\eta \frac{\partial J}{\partial K_{c}}+K_{c0}=-\eta \int_{t_{0}}^{t}e\frac{\partial e}{\partial K_{c}}d\tau +K_{c0}$

其中， $K_{c0}$ 为可调增益的初值。

将上式两边分别对时间求导数后，得到 $K_{c}$ 的变化率与广义误差 $e$ 的关系为：
$\dot{K}_{c}=-\eta e\frac{\partial e}{\partial K_{c}}$ （1.2）

上式表示了可调增益 $K_{c}\left ( t \right )$ 的自适应调整规律，只要求出 $\frac{\partial e}{\partial K_{c}}$ ，增益调整律就可确定。为此，需要确定 $e$ 关于 $K_{c}$ 的函数关系。

由系统结构图可知，参考输入 $R\left ( s \right )$ 到输出偏差 $E\left ( s \right )$ 的传递函数为：
$W_{e}\left ( s \right )=\frac{E\left ( s \right )}{R\left ( s \right )}=\left ( K_{m}-K_{c}K_{p} \right )\frac{N\left ( s \right )}{D\left ( s \right )}$

将上述拉普拉斯变换转化为微分方程描述的时域算子形式，即令：
$p=\frac{\mathrm{d} }{\mathrm{d} t},p^{2}=\frac{\mathrm{d^{2}} }{\mathrm{d} t^{2}},\cdots ,p^{n}=\frac{\mathrm{d^{n}} }{\mathrm{d} t^{n}}$

则可得到 $e$ 所满足的微分方程为：
$D\left ( p \right )e\left ( t \right )=\left ( K_{m}-K_{c}K_{p} \right )N\left ( p \right )r\left ( t \right )$

上式两端对 $K_{c}$ 求导数为：
$D\left ( p \right )\frac{\partial e}{\partial K_{c}}=-K_{p}N\left ( p \right )r\left ( t \right )$ （1.3）

另一方面，考虑到参考模型的输出与输入之间满足下列关系：
$D\left ( p \right )y_{m}\left ( t \right )=K_{m}N\left ( p \right )r\left ( t \right )$ （1.4）

令（1.3）式与（1.4）相除，并整理得：

$\frac{\partial e}{\partial K_{c}}=-\frac{K_{p}}{K_{m}}y_{m}$

将此式代入（1.2）式有：
$\dot{K}_{c}=\eta ey_{m}\frac{K_{p}}{K_{m}}$

令 $K=\eta \frac{K_{p}}{K_{m}}$ ，则有：

$\dot{K}_{c}=Key_{m}$ （1.5）

（1.5）式就是所求的可调增益 $K_{c}$ 的调节律，也就是系统的自适应规律。这种自适应规律最先由麻省理工学院提出，故又称为MIT自适应规律。

由（1.5）式可以看出，为实现这种自适应律，自适应机构由一个乘法器和一个积分器组成，具体实现的结构图如下：

这样综合出来的模型参考闭环自适应系统的数学模型可用下列一组方程来描述：

$\left\{\begin{matrix} D\left ( p \right )e\left ( t \right )=\left ( K_{m}-K_{c}K_{p} \right )N\left ( p \right )r\left ( t \right )\\ D\left ( p \right )y_{m}\left ( t \right )=K_{m}N\left ( p \right )r\left ( t \right )\\ \dot{K}_{c}=Key_{m} \end{matrix}\right.$

其中， $K> 0$ 。

MIT方案的特点：

该方案利用的是输出偏差 $e$ ，而不是状态偏差，所以自适应律所需的信号都是容易获得的，这是MIT方案额的主要优点。
这种设计方法在设计过程中并未考虑稳定性问题，不能保证所设计的自适应控制系统总是稳定的，这是它的缺点。因此，在求得自适应规律后，尚需进行稳定性校验，以确保广义误差 $e$ 在闭环回路中能收敛于某一允许的数值。

【举例1】

考虑一个一阶系统，其传递函数为 $G\left ( s \right )=\frac{K_{p}}{1+Ts}$ 。根据MIT规则设计的闭环自适应控制系统的数学模型为：

$\left\{\begin{matrix} T\dot{e}+e=\left ( K_{m}-K_{c} K_{p}\right )r\\ T\dot{y}_{m}+y_{m}=K_{m}r\\ \dot{K}_{c}=K\cdot e\cdot y_{m} \end{matrix}\right.$

假定在 $t=t_{0}$ 时， $y$ 和 $y_{m}$ 均为零，且 $K_{c}K_{p}\neq K_{m}$ 。试考察该自适应控制系统的稳定性。

【解】

假定在 $t=t_{0}$ 时给定系统输入一个幅度为 $R$ 的阶跃信号，则 $t_{0}$ 之后参考模型的输出为：

$y_{m}=K_{m}R\left ( 1-e^{-t/T} \right )$

所以自适应调节律为：

$\dot{K}_{c}=KeK_{m}R\left ( 1-e^{-t/T} \right )$

对开环广义误差方程求导数得：

$T\ddot{e}+\dot{e}=-K_{p}\dot{K}_{c}R$

或

$T\ddot{e}+\dot{e}+K_{p}KK_{m}R^{2}e\left ( 1-e^{-t/T} \right )=0$

当 $t\rightarrow \infty$ 时，上式右端第三项 $e$ 的系数趋于 $K_{p}KK_{m}R^{2}$ ，即有：

$T\ddot{e}+\dot{e}+K_{p}KK_{m}R^{2}e=0$

此系统方程是渐近稳定的，即 $t\rightarrow \infty$ 时，有： $e\rightarrow 0$ 和 $K_{c}\rightarrow \frac{K_{m}}{K_{p}}$ 。（根据劳斯判据）

结论：
对于一阶系统，按照MIT规则设计的闭环自适应系统总是稳定的。

跟踪速度或自适应速度是按指数规律进行的。理论上说，仅当 $t\rightarrow \infty$ 时，误差才趋于零，所以自适应速度是比较慢的。实际应用中，并不要求 $e$ 完全等于0。当 $\left | e \right |\leq \delta$ （ $\delta$ 为一很小的选定值）时，就认为系统已跟上参考模型了。在此意义上，自适应调整时间还是有限的。

【举例2】

设一个被控对象的传递函数为 $W_{p}\left ( s \right )=\frac{K_{p}}{a_{2}s^{2}+a_{1}s+1}$ ，理想参考模型为 $W_{m}\left ( s \right )=\frac{K_{m}}{a_{2}s^{2}+a_{1}s+1}$ 。根据MIT规则设计的闭环自适应控制系统的数学模型为：

$\left\{\begin{matrix} a_{2}\frac{\mathrm{d^{2}e} }{\mathrm{d} t^{2}}+a_{1}\frac{\mathrm{d} e}{\mathrm{d} t}+e=\left ( K_{m} -K_{p}K_{c}\right )r\\ \\ a_{2}\frac{\mathrm{d^{2}y_{m}} }{\mathrm{d} t^{2}}+a_{1}\frac{\mathrm{d} y_{m}}{\mathrm{d} t}+y_{m}=K_{m}r\\ \\ \frac{\mathrm{d}K_{c} }{\mathrm{d} t}=K\cdot e\cdot y_{m} \end{matrix}\right.$

假定在 $t=0$ 时给系统输入一个幅度为 $A$ 的阶跃信号，即 $r\left ( t \right )=A$ 。我们来研究偏差 $e$ 的稳定性。

对上式偏差微分方程的两端求导，并整理得：
$a_{2}\frac{\mathrm{d^{3}}e }{\mathrm{d} t^{3}}+a_{1}\frac{\mathrm{d^{2}}e }{\mathrm{d} t^{2}}+\frac{\mathrm{d} e}{\mathrm{d} t}=-K_{p}\frac{\mathrm{d} K_{c}}{\mathrm{d} t}A=-K_{p}Key_{m}A$

假设 $y_{m}\left ( t \right )$ 的动态响应比 $e\left ( t \right )$ 的自适应调整过程快得多。也就是说，在研究 $e\left ( t \right )$ 的调节过程时，认为 $y_{m}\left ( t \right )$ 已达到了它的稳定值 $K_{m}A$ ，那么 $e\left ( t \right )$ 的微分方程就可简化为：

$a_{2}\frac{\mathrm{d^{3}}e }{\mathrm{d} t^{3}}+a_{1}\frac{\mathrm{d^{2}}e }{\mathrm{d} t^{2}}+\frac{\mathrm{d} e}{\mathrm{d} t}+K_{m}K_{p}KA^{2}e=0$

利用劳斯（Routh）稳定性判断，易知当

$K_{m}K_{p}KA^{2}\geq \frac{a_{1}}{a_{2}}$

时，系统不稳定。也就是说，当 $K_{p}$ 满足条件上式时，输出偏差 $e$ 将出现不稳定。

上例说明，在应用局部参数最优化方法进行设计时，需要对整个系统的稳定性进行分析和检验，然而这一步工作往往是很麻烦的。

$n\leq 4$ 时的劳斯判据：
$n=1$ 时，特征方程为： $a_{0}s+a_{1}=0$ ，各系数为正。
$n=2$ 时，特征方程为： $a_{0}s^{2}+a_{1}s+a_{2}=0$ ，各系数为正。

$n=3$ 时，特征方程为： $a_{0}s^{3}+a_{1}s^{2}+a_{2}s+a_{3}=0$ ，各系数为正，且 $a_{1}a_{2}> a_{0}a_{3}$ 。

$n=4$ 时，特征方程为： $a_{0}s^{4}+a_{1}s^{3}+a_{2}s^{2}+a_{3}s+a_{4}=0$ ，各系数为正，且 $\Delta _{2}=a_{1}a_{2}-a_{0}a_{3}> 0,\Delta _{2}> \frac{a_{1}^{2}a_{4}}{a_{3}}$ 。

Kocurry

关注

37
点赞
踩
280

收藏

觉得还不错? 一键收藏
2
评论
机器人动力学与控制学习笔记（十）————自适应控制（模型参考自适应控制）

一、模型参考自适应模型参考自适应是比较流行的自适应控制方式之一。模型参考自适应控制系统的设计主要有两大类方法：一种是基于局部参数最优化的设计方法；另一种是基于稳定性理论的设计方法，包括以下两种具体的设计方法：基于Lyapunov稳定性理论的方法；基于Popov超稳定性理论和正实性概念的方法。早期的自适应控制大多采用局部参数最优化的设计方法，其主要缺点是在整个自适应过程中难以保证闭环系统的全局稳定性。而基于稳定性理论的设计方法，则从保证系统稳定性的角度出发来选择自适应规律，因此易于保证系统的稳.
复制链接

扫一扫