ransac算法_无人驾驶算法学习（一）：激光里程计之帧间匹配算法

最新推荐文章于 2024-08-20 09:15:25 发布

weixin_39856265

最新推荐文章于 2024-08-20 09:15:25 发布

阅读量890

点赞数 1

文章标签： ransac算法

转自我的csdn博客blog.csdn.net

1. 引言

激光slam主要包括前端激光里程计和后端非线性优化，由于激光雷达测量精度很高，就算没做回环和后端优化定位精度也很高。高精度地图中，里程计也是考当前帧和地图参考帧的帧间匹配算法完成位姿估计的，本文主要研究3d里程计常用的匹配算法，包括ICP算法和NDT算法。如图所示，高精度地图定位：

一般利用PCL（点云库）进行帧间匹配（点云配准，register）,介绍一下相关的类：

对应关系基类　　   pcl::CorrespondenceGrouping< PointModelT, PointSceneT >
几何相似性对应　   pcl::GeometricConsistencyGrouping< PointModelT, PointSceneT >
相似性度量　　　   pcl::recognition::HoughSpace3D
多实例对应关系　   pcl::Hough3DGrouping< PointModelT, PointSceneT, PointModelRfT,，PointSceneRfT >
CRH直方图 pcl::CRHAlignment< PointT, nbins_ >
随机采样一致性估计 pcl::recognition::ObjRecRANSAC::Output
	pcl::recognition::ObjRecRANSAC::OrientedPointPair
	pcl::recognition::ObjRecRANSAC::HypothesisCreator
	pcl::recognition::ObjRecRANSAC
	
 	pcl::recognition::ORROctree::Node::Data
  	pcl::recognition::ORROctree::Node
   	pcl::recognition::ORROctree
   	pcl::recognition::RotationSpace
ICP主要函数：
1. setInputCloud (cloud_source) 设置原始点云 
2. setInputTarget (cloud_target) 设置目标点云 
3. setMaxCorrespondenceDistance（） 设置最大对应点的欧式距离，只有对应点之间的距离小于该设置值的对应点才作为ICP计算的点对。默认值为：1.7976931348623157e+308，基本上对所有点都计算了匹配点。 
4. 三个迭代终止条件设置： 
1) setMaximumIterations（） 设置最大的迭代次数。迭代停止条件之一 
2) setTransformationEpsilon（） 设置前后两次迭代的转换矩阵的最大容差（epsilion），一旦两次迭代小于这个最大容差，则认为已经收敛到最优解，迭代停止。迭代停止条件之二，默认值为：0 
3) setEuclideanFitnessEpsilon（） 设置前后两次迭代的点对的欧式距离均值的最大容差，迭代终止条件之三，默认值为：-std::numeric_limits::max () 
迭代满足上述任一条件，终止迭代。
5.getFinalTransformation () 获取最终的配准的转化矩阵，即原始点云到目标点云的刚体变换，返回Matrix4数据类型，该数据类型采用了另一个专门用于矩阵计算的开源c++库eigen。 
6. align (PointCloudSource &output) 进行ICP配准，输出变换后点云
7. hasConverged（） 获取收敛状态，注意，只要迭代过程符合上述三个终止条件之一，该函数返回true。 
8. min_number_correspondences_  最小匹配点对数量，默认值为3，即由空间中的非共线的三点就能确定刚体变换，建议将该值设置大点，否则容易出现错误匹配。 
9. 最终迭代终止的原因可从convergence_criteria_变量中获取
注意：getFitnessScore（）用于获取迭代结束后目标点云和配准后的点云的最近点之间距离的均值。

2. ICP算法

ICP(Iterative Closest Point )原理：假设两个点云数据集合P和G，要通过P转换到G（假设两组点云存在局部几何特征相似的部分），可以通过P叉乘四元矩阵进行旋转平移变换到G，或者SVD法将P转换到G位置，总体思想都是需要一个4x4的旋转平移矩阵。对于每次旋转平移变换后计算P的所有（采样）点到G对应（最近）点的距离，用最小二乘法（求方差）求出最小二乘误差，看是否在要求的范围内，如果最小二乘误差小于设定的值，（或迭代次数达到上限，或每次重新迭代后最小二乘误差总在一个很小的范围内不再发生变化），则计算结束，否则继续进行迭代。

缺点：

算法收敛于局部最小误差。
噪声或异常数据可能导致算法无法收敛或错误。
在进行ICP算法第一步要确定一个迭代初值，选取的初值将对最后配准结果产生重要的影响，如果初值选择不合适，算法可能就会限入局部最优。

2.改进：

加快搜索效率：K-D树
CSM（Canonical Scan Matcher）[1]
点到线 PL-ICP[2]
点到面 PP-ICP[3]

2.1 Point to Plane ICP

Point-to-Plane ICP(点面ICP)原理：

测量点到平面的距离作为目标函数，point-to-plane会比point-to-point收敛的更快，但是对point-to-plane的优化是一个非线性问题，速度比较慢。不过幸运的是，我们可以用线性优化来近似。

1. 示意图：

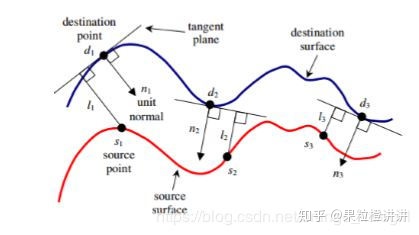
2. 目标函数：

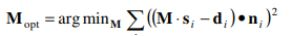
式中，s为当前帧中任意一点，d为参考帧与之对应的一点，n为参考点所在面的法向量，M是一个4*4的3D刚体变换矩阵，3D刚体变换M是由旋转和平移构成的。

且R中参数满足：

要最小化point-to-plane目标函数，只有6个参数：α,β,γ,tx,ty,tzα,β,γ,tx,ty,tz，但是其中的α,β,γα,β,γ与非线性函数cos，sin有关。因此比较难求解。

：

代入线性化的目标函数得：

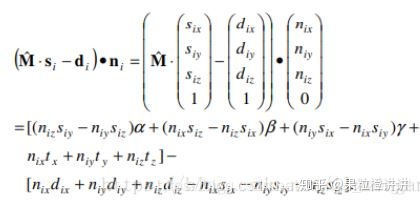
2.2 代码实战

代码分析如下：

#include <pcl/registration/icp.h>
  // Subscribers订阅话题
  ros::Subscriber param_sub = nh.subscribe("config/icp", 10, param_callback);//设置icp的参数
  ros::Subscriber gnss_sub = nh.subscribe("gnss_pose", 10, gnss_callback);//订阅gnss，回调函数：更新gnss的位姿
  ros::Subscriber map_sub = nh.subscribe("points_map", 10, map_callback);//订阅地图，回调：寻找icp的参考帧
  ros::Subscriber initialpose_sub = nh.subscribe("initialpose", 1000, initialpose_callback);//订阅带有协方差的初始值
  ros::Subscriber points_sub = nh.subscribe("filtered_points", _queue_size, points_callback);//订阅过滤后的当前点云，回调：设置当前参考帧进行icp匹配
  static void map_callback(const sensor_msgs::PointCloud2::ConstPtr& input)
  {
	  ..........
	  icp.setInputTarget(map_ptr);//参考帧
	  ..........
	  }
  	static void points_callback(const sensor_msgs::PointCloud2::ConstPtr& input)//icp核心算法
 {
 .	........
  	icp.setInputSource(filtered_scan_ptr);//输入的当前点云帧
	.........
	//设置ICP参数
	icp.setMaximumIterations(maximum_iterations);//最大迭代次数
	icp.setTransformationEpsilon(transformation_epsilon);//最大转化矩阵差值
	icp.setMaxCorrespondenceDistance(max_correspondence_distance);//最大欧式距离差值
	icp.setEuclideanFitnessEpsilon(euclidean_fitness_epsilon);//收敛条件是均方误差和小于阈值， 停止迭代。
	icp.setRANSACOutlierRejectionThreshold(ransac_outlier_rejection_threshold);//剔除错误估计，可用 RANSAC 算法，或减少数量
	icp.align(*output_cloud, init_guess);//进行ICP配准，输出变换后点云
	
	t = icp.getFinalTransformation();  // localizer，得的最后的4x4变换矩阵
	.........


}

利用Point to Plane ICP进行优化，查看pcl相关类的参考资料

#include <pcl/registration/transformation_estimation_point_to_plane_lls.h>#头文件
ptp_icp=TransformationEstimationPointToPlaneLLS< PointSource, PointTarget, Scalar >::TransformationEstimationPointToPlaneLLS ();
//<PointSource, PointTarget, Scalar>模板的参数类型，提前定义
ptp_icp.estimateRigidTransformation<PointSource, PointTarget, Scalar>(const pcl::PointCloud< PointSource > & 
cloud_src,const pcl::PointCloud< PointTarget > &cloud_tgt ,M);//输入：当前帧和参考的地图帧   输出：M变换矩阵
//##函数重载，参数不一样实现不一样(alpha,beta,gamma,tx,ty,tz,M)

3. NDT算法

正态分布变换（NDT）算法是一个配准算法[4]，它应用于三维点的统计模型，使用标准最优化技术来确定两个点云间的最优的匹配，因为其在配准过程中不利用对应点的特征计算和匹配，所以时间比其他方法快。

3.1 数学原理

NDT算法的基本思想是先根据参考数据（reference scan）来构建多维变量的正态分布，如果变换参数能使得两幅激光数据匹配的很好，那么变换点在参考系中的概率密度将会很大。因此，可以考虑用优化的方法求出使得概率密度之和最大的变换参数，此时两幅激光点云数据将匹配的最好。

step1.将参考点云（reference scan）所占的空间划分成指定大小（CellSize）的网格或体素（Voxel）；并计算每个网格的多维正态分布参数：

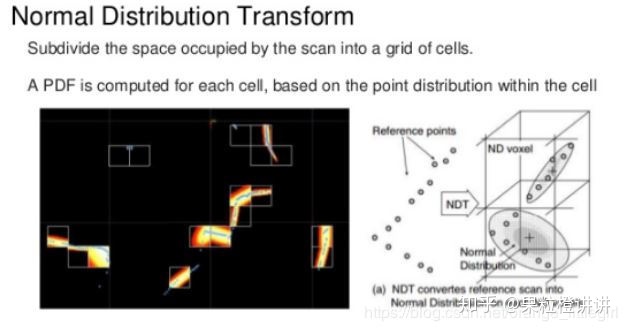
参考帧每个最小格子中的点云都满足Guassian分布，计算均值和方差

1.均值

2.协方差矩阵

step2. 初始化变换参数
（赋予零值或者使用里程计数据赋值，
此处只考虑二维激光雷达）
step3. 对于要配准的点云（second scan），通过变换T将其转换到参考点云的网格中

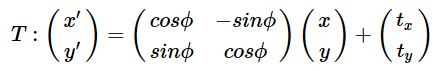
step4. 根据参考帧的正态分布参数，计算当前帧每个转换点的概率密度（probability density function, PDF）

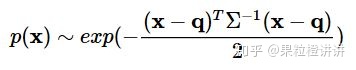
step5. NDT配准得分（score），每个点云可能会占据多个网格，通过对每个网格计算出的概率密度相加得总分

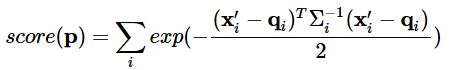
step6. 根据牛顿优化算法对目标函数-score进行优化，即寻找变换参数$p$使得score的值最大。优化的关键步骤是要计算目标函数(-score)的梯度和Hessian矩阵（此处海塞矩阵不难算，若是视觉slam中用高斯牛顿优化）：

注意：可以当做表面的近似表达，协方差矩阵的特征向量和特征值可以表达表面信息（朝向、平整度），格子内少于3个点，经常会协方差矩阵不存在逆矩阵，所以只计算点数大于5的cell，涉及到下采样方法。下图是一个3D点云及其网格化效果:

上图中立方体的边长为 1 米，其中越明亮的位置表示概率越高。此外，局部表面的方向和光滑性则可以通过协方差矩阵的特征值和特征向量反映出来。我们以三维的概率密度函数为例，如果三个特征值很接近，那么这个正态分布描述的表面是一个球面，如果一个特征值远大于另外两个特征值，则这个正态分布描述的是一条线，如果一个特征值远小于另外两个特征值，则这个正态分布描述的是一个平面。下图描述了协方差矩阵特征值和表面形状之间的关系：

NDT缺点：格子参数最重要，太大导致精度不高，太小导致内存过高，并且只有两幅图像相差不大的情况才能匹配

改进：

1. 八叉树建立，格子有大有小，迭代，每次使用更精细的格子

2. K聚类，有多少个类就有多少个cell，格子大小不一

3. 三线插值平滑相邻的格子cell导致的不连续，提高精度

3.2 代码实战

Autoware的点云定位模块中代码分析：

#ifdef USE_FAST_PCL
   #include <fast_pcl/registration/ndt.h>
 #else
   #include <pcl/registration/ndt.h>
 #endif
#ifdef CUDA_FOUND
  #include <fast_pcl/ndt_gpu/NormalDistributionsTransform.h>
 #endif

	...........核心算法代码，构建地图使用ndt算法
	static std::shared_ptr<gpu::GNormalDistributionsTransform> new_gpu_ndt_ptr = std::make_shared<gpu::GNormalDistributionsTransform>();//创建NDT转换矩阵类
	new_gpu_ndt_ptr->setResolution(ndt_res);//网格大小设置
	new_gpu_ndt_ptr->setInputTarget(map_ptr);//参考帧
	new_gpu_ndt_ptr->setMaximumIterations(max_iter);//迭代最大次数
	new_gpu_ndt_ptr->setStepSize(step_size);//牛顿法优化的最大步长
	new_gpu_ndt_ptr->setTransformationEpsilon(trans_eps);//连续变换之间允许的最大差值

	pcl::PointCloud<pcl::PointXYZ>::Ptr dummy_scan_ptr(new pcl::PointCloud<pcl::PointXYZ>());
	pcl::PointXYZ dummy_point;
 	dummy_scan_ptr->push_back(dummy_point);//构建地图map
	new_gpu_ndt_ptr->setInputSource(dummy_scan_ptr);//当前帧
	
	new_ndt.omp_align(*output_cloud, Eigen::Matrix4f::Identity());
	fitness_score = ndt.omp_getFitnessScore();
	t = ndt.getFinalTransformation();
	// Update localizer_pose
	localizer_pose.x = t(0, 3);
	localizer_pose.y = t(1, 3);
	localizer_pose.z = t(2, 3);
	
.	.........

 
 -------------使用ndt算法与地图参考帧进行匹配---------------举一个列子gpu_ndt_ptr->setInputSource（），其他和地图一致

#ifdef CUDA_FOUND//在代码中标记可以用GPU并行加速
if (_use_gpu == true)
{
	gpu_ndt_ptr->setInputSource(filtered_scan_ptr);//参考点云
}
else
{
#endif
	if (_use_fast_pcl)
	{
		cpu_ndt.setInputSource(filtered_scan_ptr);
	}
	else
	{
		ndt.setInputSource(filtered_scan_ptr);
	}
#ifdef CUDA_FOUND	
}
#endif

//NDT默认值设置
static int max_iter = 30;        // 最大迭代次数
static float ndt_res = 1.0;      // 分辨率1m
static double step_size = 0.1;   // 步长0.1m
static double trans_eps = 0.01;  // 变换矩阵差值

其中 ndt.setTransformationEpsilon() 即设置变换的 ϵ（两个连续变换之间允许的最大差值），这是判断我们的优化过程是否已经收敛到最终解的阈值。ndt.setStepSize(0.1) 即设置牛顿法优化的最大步长。ndt.setResolution(1.0) 即设置网格化时立方体的边长，网格大小设置在NDT中非常重要，太大会导致精度不高，太小导致内存过高，并且只有两幅点云相差不大的情况才能匹配。ndt.setMaximumIterations(30) 即优化的迭代次数，我们这里设置为35次，即当迭代次数达到35次或者收敛到阈值时，停止优化。由于NDT算法不需要匹配各个点计算速度较ICP快，官方建议定位模块使用NDT算法，然后通过使用CUDA实现的 fast_pcl package实现了对NDT优化过程的。

参考文献：

[1] 源码 Andrea Censi's website

[2] An ICP variant using a point-to-line metric

[3] Linear Least-Squares Optimization for Point-to-Plane ICP Surface Registration

[4] The Normal Distributions Transform: A New Approach to Laser Scan Matching