运用:比如有一种是在回环的时候,像视觉中的回环是根据词袋等描述符进行匹配的,所以即使漂移的很严重,也能基本回环成功,但是在激光回环中,是根据不确定的经验值划一个范围框,然后在这个框里面进行回环检测,此时如果帧间匹配做的很差的话,那这个框就需要划的很大,由此带来的缺点就是:计算量大、可区分性太低,导致错误的回环。
帧间匹配算法
不一定都是前后帧之间(即scan-to-scan),也可以是(scan-to-map)
1. ICP匹配方法
本方法已经在上一篇博客中进行了介绍,这篇博客里面只记录已知匹配对应点情况下的一个具体求解过程。
- 目的:是能使误差函数 E ( R , t ) = 1 N p ∑ i = 1 N p ∥ x i − R p i − t ∥ 2 E(R, t)=\frac{1}{N_{p}} \sum_{i=1}^{N_{p}}\left\|x_{i}-R p_{i}-t\right\|^{2} E(R,t)=Np1∑i=1Np∥xi−Rpi−t∥2最小时的R,t
- 进行公式变换,其中
u
x
和
u
p
u{_x}和u{_p}
ux和up是两个点云的中心坐标:
- E ( R , t ) = 1 N p ∑ i = 1 N p ∥ x i − R p i − t ∥ 2 = 1 N p ∑ i = 1 N p ∥ x i − R p i − t − u x + R u p + u x − R u p ∥ 2 = 1 N p ∑ i = 1 N p ∥ x i − u x − R ( p i − u p ) + ( u x − R u p − t ) ∥ 2 = 1 N p ∑ i = 1 N p ( ∥ x i − u x − R ( p i − u p ) ∥ 2 + ∥ u x − R u p − t ∥ 2 + 2 ( x i − u x − R ( p i − u p ) ) T ( u x − R u p − t ) ) \begin{array}{l} E(R, t)=\frac{1}{N_{p}} \sum_{i=1}^{N_{p}}\left\|x_{i}-R p_{i}-t\right\|^{2}\\ =\frac{1}{N_{p}} \sum_{i=1}^{N_{p}}\left\|x_{i}-R p_{i}-t-u_{x}+R u_{p}+u_{x}-R u_{p}\right\|^{2} \\ =\frac{1}{N_{p}} \sum_{i=1}^{N_{p}}\left\|x_{i}-u_{x}-R\left(p_{i}-u_{p}\right)+\left(u_{x}-R u_{p}-t\right)\right\|^{2} \\ =\left.\frac{1}{N_{p}} \sum_{i=1}^{N_{p}}(\left\|x_{i}-u_{x}-R\left(p_{i}-u_{p}\right)\right\|^{2}+\| u_{x}-R u_{p}-t\right \|^{2} \left.+2\left(x_{i}-u_{x}-R\left(p_{i}-u_{p}\right)\right)^{T}\left(u_{x}-R u_{p}-t\right)\right) \end{array} E(R,t)=Np1∑i=1Np∥xi−Rpi−t∥2=Np1∑i=1Np∥xi−Rpi−t−ux+Rup+ux−Rup∥2=Np1∑i=1Np∥xi−ux−R(pi−up)+(ux−Rup−t)∥2=Np1∑i=1Np(∥xi−ux−R(pi−up)∥2+∥ux−Rup−t∥ ∥2+2(xi−ux−R(pi−up))T(ux−Rup−t))
- 其中最后一项 2 ( x i − u x − R ( p i − u p ) ) T ( u x − R u p − t ) 2\left(x_{i}-u_{x}-R\left(p_{i}-u_{p}\right)\right)^{T}\left(u_{x}-R u_{p}-t\right) 2(xi−ux−R(pi−up))T(ux−Rup−t)在乘以 1 N p ∑ i = 1 N p \frac{1}{N_{p}} \sum_{i=1}^{N_{p}} Np1∑i=1Np后,分配进去会等于0.
- 则原式就为 E ( R , t ) = 1 N p ∑ i = 1 N p ( ∥ x i − u x − R ( p i − u p ) ∥ 2 + ∥ u x − R u p − t ) ∥ 2 ) E(R, t)=\frac{1}{N_{p}} \sum_{i=1}^{N_{p}}(\left\|x_{i}-u_{x}-R\left(p_{i}-u_{p}\right)\right\|^{2}+\| u_{x}-R u_{p}-t) \|^{2}) E(R,t)=Np1∑i=1Np(∥xi−ux−R(pi−up)∥2+∥ux−Rup−t)∥2),观察可得知,前一项只与R有关,故只要能先得到R,那就可以由第二个得到t,那此时先对第一项求最小二乘得到R。
- 此时目标函数就变成 E ( R , t ) = 1 N p ∑ i = 1 N p ∥ x i − u x − R ( p i − u p ) ∥ 2 = 1 N p ∑ i = 1 N p ∥ x i ′ − R p i ′ ∥ 2 = 1 N p ∑ i = 1 N p x i ′ T x i ′ + p i ′ T R T R p i ′ − 2 x i ′ T R p i ′ \begin{array}{l} E(R, t)=\frac{1}{N_{p}} \sum_{i=1}^{N_{p}}\left\|x_{i}-u_{x}-R\left(p_{i}-u_{p}\right)\right\|^{2} \\ =\frac{1}{N_{p}} \sum_{i=1}^{N_{p}}\left\|x_{i}^{\prime}-R p_{i}^{\prime}\right\|^{2}=\frac{1}{N_{p}} \sum_{i=1}^{N_{p}} x_{i}^{\prime T} x_{i}^{\prime}+p_{i}^{\prime T} R^{T} R p_{i}^{\prime}-2 x_{i}^{\prime T} R p_{i}^{\prime} \end{array} E(R,t)=Np1∑i=1Np∥xi−ux−R(pi−up)∥2=Np1∑i=1Np∥xi′−Rpi′∥2=Np1∑i=1Npxi′Txi′+pi′TRTRpi′−2xi′TRpi′,其中 x i ′ 和 p i ′ x_{i}^{\prime}和p_{i}^{\prime} xi′和pi′是去中心化坐标(详见上一篇博客)
- 在上式中,第一项为常数,第二项中因为R是正交矩阵, R T R R^TR RTR是单位矩阵,故也是常数,所以就只剩下最后一项,并且要求一个负数的最小值,就是要求对应相反数的最大值,则目标函数就变成:
- ∑ i = 1 N p x i ′ T R p i ′ = ∑ i = 1 N p Trace ( R x i ′ p i ′ T ) = Trace ( R H ) \sum_{i=1}^{N_{p}} x_{i}^{\prime T} R p_{i}^{\prime}=\sum_{i=1}^{N_{p}} \operatorname{Trace}\left(R x_{i}^{\prime} p_{i}^{\prime T}\right)=\operatorname{Trace}(R H) ∑i=1Npxi′TRpi′=∑i=1NpTrace(Rxi′pi′T)=Trace(RH),其中 H = ∑ i = 1 N p x i ′ p i ′ T H=\sum_{i=1}^{N_{p}} x_{i}^{\prime} p_{i}^{\prime T} H=∑i=1Npxi′pi′T
- 最后使用以下定理得到结果

但是在实际工程中不可能知道两个点云的点是如何配对的。只能通过迭代求解的方法一步步缩小误差,最终得到使误差方程最小的旋转矩阵R和平移矩阵t。
所以具体一般实现的算法流程是:
- a.寻找对应匹配点:一般使用里程计等得到的一个初始位姿转换来帮助寻找点的匹配(注意坐标系)
- b.得到匹配点后,就进行上面的R和t求解流程。
- c.将得到的R和t用于下次迭代的初始值,直到误差小于设定的阈值
2. PL-ICP匹配方法
因为激光点数据的弊端,即当打到的是同物体的两个相似的部位时,会给它匹配上,这就导致会引入随机误差,所以就引入PL-ICP。
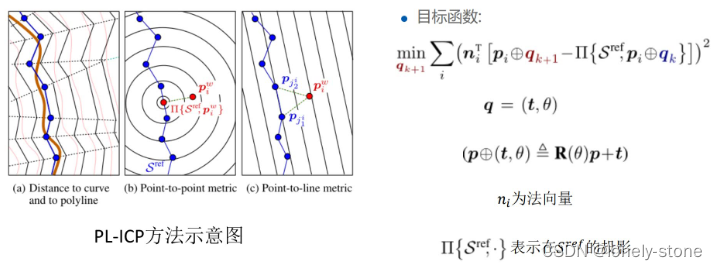
- 算法流程:
- a.给定一个初始的转换矩阵,将当前激光帧的数据转换到参考帧坐标系下。初始的转换矩阵 一般通过里程计来获得。而后面迭代计算所需的转换矩阵由上一次算法迭代计算得到。
- b.对于当前帧的点i,在参考帧中找到两个最近的点 ( j 1 , j 2 (j{_1},j{_2} (j1,j2。
- c.计算误差,并去除误差过大的点。
- d.最小化误差函数: ∑ i ( n i T [ R ( θ k + 1 ) p i + t k + 1 − p j 1 ] ) 2 \sum_{i}\left(\boldsymbol{n}_{i}^{\mathrm{T}}\left[\mathbf{R}\left(\theta_{k+1}\right) \boldsymbol{p}_{i}+\boldsymbol{t}_{k+1}-\boldsymbol{p}_{j_{1}}\right]\right)^{2} ∑i(niT[R(θk+1)pi+tk+1−pj1])2
- e.得到RT,进行下一次迭代
- 跟ICP的区别:
- a.误差函数形式不同,ICP是点到点距离做误差,PL-ICP是点到线作为误差。
- b.收敛速度不同,ICP一阶收敛,PL-ICP二阶收敛
- c.PL-ICP精度更高,更贴近现实情况
- d.PL-ICP对初始值更敏感
3.基于优化的匹配算法
(HectorSLAM,cartographer)
目标函数:把激光的帧间匹配问题转换为求解目标函数的极值问题
- E ( T ) = arg min T ∑ [ 1 − M ( S i ( T ) ) ] 2 其中 T = ( T x , T y , T θ ) S i ( T ) 表示把当前每束激光数据用位姿转换到世界坐标系或者是要进行比对的地图坐标系下 M ( x ) 表示得到坐标 x 的地图占用概率(似然得分) E(T)=\arg \min _{T} \sum\left[1-M\left(S_{i}(T)\right)\right]^{2}\\ 其中T=\left(T_{x}, T_{y}, T_{\theta}\right)\\ S_{i}(T)表示把当前每束激光数据用位姿转换到世界坐标系或者是要进行比对的地图坐标系下\\ M(x)表示得到坐标x的地图占用概率(似然得分) E(T)=argminT∑[1−M(Si(T))]2其中T=(Tx,Ty,Tθ)Si(T)表示把当前每束激光数据用位姿转换到世界坐标系或者是要进行比对的地图坐标系下M(x)表示得到坐标x的地图占用概率(似然得分)
非线性函数的求解步骤:
- 目标函数中的 S i ( T ) = [ cos T θ − sin T θ T x sin T θ cos T θ T y 0 0 1 ] [ p i x p i y 1 ] S_{i}(T)=\left[\begin{array}{ccc} \cos T_{\theta} & -\sin T_{\theta} & T_{x} \\ \sin T_{\theta} & \cos T_{\theta} & T_{y} \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} p_{i x} \\ p_{i y} \\ 1 \end{array}\right] Si(T)=⎣ ⎡cosTθsinTθ0−sinTθcosTθ0TxTy1⎦ ⎤⎣ ⎡pixpiy1⎦ ⎤,其中 p i = ( p i x , p i y ) p_{i}=\left(p_{i x}, p_{i y}\right) pi=(pix,piy)表示第i个激光点的坐标。
- 因为 M ( S i ( T ) ) M(S_{i}(T)) M(Si(T))是非线性函数,不能直接求导,由此对其进行一阶泰勒展开,得: E ( T + Δ T ) = arg min Δ T ∑ [ 1 − M ( S i ( T ) ) − ∇ M ( S i ( T ) ) ∂ S i ( T ) ∂ T Δ T ] 2 E(T+\Delta T)=\arg \min _{\Delta T} \sum\left[1-M\left(S_{i}(T)\right)-\nabla M\left(S_{i}(T)\right) \frac{\partial S_{i}(T)}{\partial T} \Delta T\right]^{2} E(T+ΔT)=argminΔT∑[1−M(Si(T))−∇M(Si(T))∂T∂Si(T)ΔT]2
- 泰勒展开得到线性函数后,就可以对其 Δ T \Delta T ΔT求导,并令其为零: ∑ [ ∇ M ( S i ( T ) ) ∂ S i ( T ) ∂ T ] T [ 1 − M ( S i ( T ) ) − ∇ M ( S i ( T ) ) ∂ S i ( T ) ∂ T Δ T ] = 0 \sum\left[\nabla M\left(S_{i}(T)\right) \frac{\partial S_{i}(T)}{\partial T}\right]^{T}\left[1-M\left(S_{i}(T)\right)-\nabla M\left(S_{i}(T)\right) \frac{\partial S_{i}(T)}{\partial T} \Delta T\right] = 0 ∑[∇M(Si(T))∂T∂Si(T)]T[1−M(Si(T))−∇M(Si(T))∂T∂Si(T)ΔT]=0
- 求解上式得到 Δ T \Delta T ΔT,并令 T = T + Δ T T = T + \Delta T T=T+ΔT,不断迭代
补充:
- 补1(上面导数为0的具体求解过程): ∑ [ ∇ M ( S i ( T ) ) ∂ S i ( T ) ∂ T ] T [ 1 − M ( S i ( T ) ) − ∇ M ( S i ( T ) ) ∂ S i ( T ) ∂ T Δ T ] = 0 展开得 : ∑ [ ∇ M ( S i ( T ) ) ∂ S i ( T ) ∂ T ] T [ 1 − M ( S i ( T ) ) ] = ∑ [ ∇ M ( S i ( T ) ) ∂ S i ( T ) ∂ T ] T [ ∇ M ( S i ( T ) ) ∂ S i ( T ) ∂ T Δ T ] 等式两边同时乘以 H − 1 : Δ T = H − 1 ∑ [ ∇ M ( S i ( T ) ) ∂ S i ( T ) ∂ T ] T [ 1 − M ( S l ( T ) ) ] 其中 H = ∑ [ ∇ M ( S i ( T ) ) ∂ S i ( T ) ∂ T ] T [ ∇ M ( S i ( T ) ) ∂ S i ( T ) ∂ T ] \sum\left[\nabla M\left(S_{i}(T)\right) \frac{\partial S_{i}(T)}{\partial T}\right]^{T}\left[1-M\left(S_{i}(T)\right)-\nabla M\left(S_{i}(T)\right) \frac{\partial S_{i}(T)}{\partial T} \Delta T\right]=0\\ 展开得:\sum\left[\nabla M\left(S_{i}(T)\right) \frac{\partial S_{i}(T)}{\partial T}\right]^{T}\left[1-M\left(S_{i}(T)\right)\right]=\sum\left[\nabla M\left(S_{i}(T)\right) \frac{\partial S_{i}(T)}{\partial T}\right]^{T}\left[\nabla M\left(S_{i}(T)\right) \frac{\partial S_{i}(T)}{\partial T} \Delta T\right]\\ 等式两边同时乘以 H^{-1} : \begin{array}{l} \Delta T=H^{-1} \sum\left[\nabla M\left(S_{i}(T)\right) \frac{\partial S_{i}(T)}{\partial T}\right]^{T}\left[1-M\left(S_{l}(T)\right)\right] \\ 其中H=\sum\left[\nabla M\left(S_{i}(T)\right) \frac{\partial S_{i}(T)}{\partial T}\right]^{T}\left[\nabla M\left(S_{i}(T)\right) \frac{\partial S_{i}(T)}{\partial T} \right] \end{array} ∑[∇M(Si(T))∂T∂Si(T)]T[1−M(Si(T))−∇M(Si(T))∂T∂Si(T)ΔT]=0展开得:∑[∇M(Si(T))∂T∂Si(T)]T[1−M(Si(T))]=∑[∇M(Si(T))∂T∂Si(T)]T[∇M(Si(T))∂T∂Si(T)ΔT]等式两边同时乘以H−1:ΔT=H−1∑[∇M(Si(T))∂T∂Si(T)]T[1−M(Sl(T))]其中H=∑[∇M(Si(T))∂T∂Si(T)]T[∇M(Si(T))∂T∂Si(T)]
- 补2( 求解 Δ T 中的 ∂ S i ( T ) ∂ T ) 求解\Delta T中的\frac{\partial S_{i}(T)}{\partial T}) 求解ΔT中的∂T∂Si(T))): 已知 S i ( T ) = [ cos T θ − sin T θ T x sin T θ cos T θ T y 0 0 1 ] [ p i x p i y 1 ] = [ cos T θ ∗ p i x − sin T θ ∗ p i y + T x sin T θ ∗ p i x + cos T θ ∗ p i y + T y 1 ] − 则 S i ( T ) 对 T = ( T x , T y , T θ ) 求导得: ∂ S i ( T ) ∂ T = [ 1 0 − sin T θ ∗ p i x − cos T θ ∗ p i y 0 1 cos T θ ∗ p i x − sin T θ ∗ p i y ] 已知S_{i}(T)=\left[\begin{array}{ccc} \cos T_{\theta} & -\sin T_{\theta} & T_{x} \\ \sin T_{\theta} & \cos T_{\theta} & T_{y} \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} p_{i x} \\ p_{i y} \\ 1 \end{array}\right] = \left[\begin{array}{c} \cos T_{\theta} * p_{i x}-\sin T_{\theta} * p_{i y}+T_{x} \\ \sin T_{\theta} * p_{i x}+\cos T_{\theta} * p_{i y}+T_{y} \\ 1 \end{array}\right]\\ - \\ 则S_{i}(T)对T=(T{_x},T{_y},T{_\theta})求导得:\frac{\partial S_{i}(T)}{\partial T}=\left[\begin{array}{ccc} 1 & 0 & -\sin T_{\theta} * p_{i x}-\cos T_{\theta} * p_{i y} \\ 0 & 1 & \cos T_{\theta} * p_{i x}-\sin T_{\theta} * p_{i y} \end{array}\right] 已知Si(T)=⎣ ⎡cosTθsinTθ0−sinTθcosTθ0TxTy1⎦ ⎤⎣ ⎡pixpiy1⎦ ⎤=⎣ ⎡cosTθ∗pix−sinTθ∗piy+TxsinTθ∗pix+cosTθ∗piy+Ty1⎦ ⎤−则Si(T)对T=(Tx,Ty,Tθ)求导得:∂T∂Si(T)=[1001−sinTθ∗pix−cosTθ∗piycosTθ∗pix−sinTθ∗piy]
- 现在 Δ T 表达式中所有的量都已经知道 , 除了 ∇ M ( S i ( T ) ) , S i ( T ) 表示地图坐标点 , ∇ M ( S i ( T ) ) 表示地图的导数 ( 地图梯度) , 而 ∇ M ( S i ( T ) ) 的求解需要对地图进行揷值(因为地图是离散的) 现在\Delta T表达式中所有的量都已经知道, 除了 \nabla M\left(S_{i}(T)\right) , S_{i}(T)表示地图坐标点, \nabla M\left(S_{i}(T)\right) 表示地图的导数(地图梯度) ,而\nabla M\left(S_{i}(T)\right)的求解需要对地图进行揷值(因为地图是离散的) 现在ΔT表达式中所有的量都已经知道,除了∇M(Si(T)),Si(T)表示地图坐标点,∇M(Si(T))表示地图的导数(地图梯度),而∇M(Si(T))的求解需要对地图进行揷值(因为地图是离散的)
- 补3( 求解 Δ T 中的 ∇ M ( S i ( T ) ) 求解\Delta T中的\nabla M\left(S_{i}(T)\right) 求解ΔT中的∇M(Si(T))):
地图插值:
- 地图插值采用双线性插值,而双线性插值由一维线性插值推广而来,其中拉格朗日插值法就是一维线性插值。
- 插值的定义:设
y
=
f
(
x
)
y = f(x)
y=f(x)在区间[a, b]上有定义,且存在已知点:
a
≤
x
0
<
x
1
<
⋯
<
x
n
≤
b
a \leq x_{0}<x_{1}<\cdots<x_{n} \leq b
a≤x0<x1<⋯<xn≤b,并且对应的函数值
y
i
=
f
(
x
i
)
y{_i} = f(x{_i})
yi=f(xi)。
若存在n次多项式 L n ( x ) = a 0 + a 1 x + a 2 x 2 + ⋯ + a n x n L_{n}(x)=a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} Ln(x)=a0+a1x+a2x2+⋯+anxn,使得 L n ( x i ) = y i L{_n}(x{_i}) = y{_i} Ln(xi)=yi成立,则称 L n ( x ) L{_n}(x) Ln(x)为f(x)的插值多项式。(数学上可知,这个多项式存在且唯一) - 而拉格朗日就是把插值多项式表示成基函数的线性组合:
L
n
(
x
)
=
∑
i
=
0
n
l
i
(
x
)
y
i
L_{n}(x)=\sum_{i=0}^{n} l_{i}(x) y_{i}
Ln(x)=∑i=0nli(x)yi,并且基函数
l
i
(
x
)
l_{i}(x)
li(x)满足:
l
i
(
x
k
)
=
{
1
k
=
i
0
k
≠
i
l_{i}\left(x_{k}\right)=\left\{\begin{array}{ll} 1 & k=i \\ 0 & k \neq i \end{array}\right.
li(xk)={10k=ik=i
即基函数 l i ( x ) l_{i}(x) li(x)在除 x i x{_i} xi以外的函数值都为0,所以 ( x 0 , 0 ) , ( x 1 , 0 ) , ( x 2 , 0 ) , . . . . . , ( x n , 0 ) (不包括 x i ) (x{_0}, 0),(x{_1}, 0),(x{_2}, 0),.....,(x{_n}, 0)(不包括x_i) (x0,0),(x1,0),(x2,0),.....,(xn,0)(不包括xi),都是 l i ( x ) l_{i}(x) li(x)的解,则此时可以构造函数:
l i ( x ) − 0 = c ( x − x 0 ) ⋯ ( x − x i − 1 ) ( x − x i + 1 ) ( x − x n ) l_{i}(x) - 0=c\left(x-x_{0}\right) \cdots\left(x-x_{i-1}\right)\left(x-x_{i+1}\right)\left(x-x_{n}\right) li(x)−0=c(x−x0)⋯(x−xi−1)(x−xi+1)(x−xn)
把点 ( x i , 0 ) (x_i,0) (xi,0)代入构造的函数得:
l i ( x i ) = c ( x i − x 0 ) ⋯ ( x i − x i − 1 ) ( x i − x i + 1 ) ( x i − x n ) = 1 l_{i}\left(x_{i}\right)=c\left(x_{i}-x_{0}\right) \cdots\left(x_{i}-x_{i-1}\right)\left(x_{i}-x_{i+1}\right)\left(x_{i}-x_{n}\right)=1 li(xi)=c(xi−x0)⋯(xi−xi−1)(xi−xi+1)(xi−xn)=1
最后, c = 1 ( x i − x 0 ) ⋯ ( x i − x i − 1 ) ( x i − x i + 1 ) ( x i − x n ) l i ( x ) = ∏ k = 0 , k ≠ i n x − x k ( x i − x k ) c=\frac{1}{\left(x_{i}-x_{0}\right) \cdots\left(x_{i}-x_{i-1}\right)\left(x_{i}-x_{i+1}\right)\left(x_{i}-x_{n}\right)} \quad l_{i}(x)=\prod_{k=0, k \neq i}^{n} \frac{x-x_{k}}{\left(x_{i}-x_{k}\right)} c=(xi−x0)⋯(xi−xi−1)(xi−xi+1)(xi−xn)1li(x)=∏k=0,k=in(xi−xk)x−xk - 双线性插值

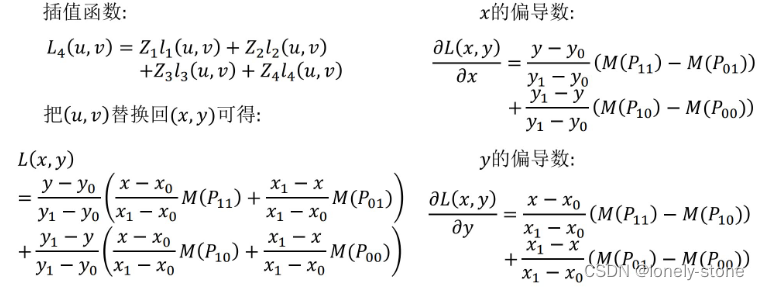
基于优化的方法对初值敏感,精度高
4. 相关匹配方法及分枝定界加速
关于相关方法,cartographer在用
- 帧间匹配似然场:

由图中可知,函数是高度非凸,存在很多局部极值,所以对初值非常敏感。
相关法就是进行暴力匹配,排除初值影响;然后可以通过加速策略,降低计算量;计算位姿匹配的方差。 - 算法流程
- a.构建似然场(高斯平滑)
- b.在指定的搜索空间内,进行搜索,计算每个位姿的得分,并进行一个得分的排序
- c.根据步骤b中位姿的得分,计算本次位姿匹配的方差。
- 位姿搜索(步骤b)
-
1.暴力搜索
( x , y , θ ) (x,y,\theta) (x,y,θ)进行三层for循环枚举每个位姿,分别计算每个位姿的得分,计算量巨大,因为激光雷达数据在每个位姿当中都要进行重新投影(这期间需要反复算sin和cos函数)。 -
2.预先投影搜索
-
3.多分辨率搜索
-























 3115
3115











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








